第九章 字符串算法(2021/11/27-by-tycube)
9.1 精确字符串匹配
9.1.1 问题描述:
- 给定文本 T T T和模式 P P P,要求返回文本 T T T能对应上模式 P P P的第一个位置,即满足 T [ s . . . s + m ? 1 ] = P [ 0... m ? 1 ] T[s...s+m-1]=P[0...m-1] T[s...s+m?1]=P[0...m?1]时 T [ s ] T[s] T[s]的最小下标.

9.1.2 解题思路:
1. 暴力搜索
2. Rabin-Karp算法
2.1 基本思想:基于指纹的思想。
-
指纹思想:对于给定的T和P,通过函数处理成可以直接进行比较的值(计算代价 O ( m ) O(m) O(m)),称其为指纹。指纹相同、字符串不一定完全匹配,但指纹不相同说明字符串一定不匹配。
-
需要注意的是,模式P的指纹是固定的,但文本T对应位置的指纹无需每次完全重新计算,可以直接计算(进制一般为十进制)
(已知的指纹值-最高位的数x当前进制^{所处位数})x进制+新加入的数字x进制 -
如图所示:
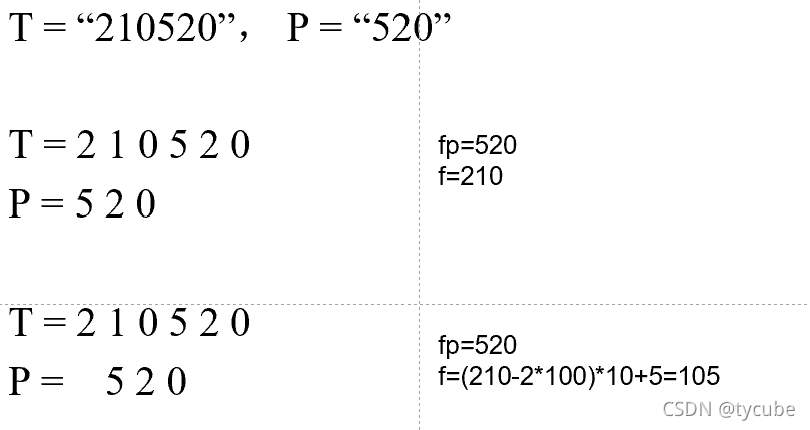
-
指纹计算:可以通过使用哈希函数 h = f m o d q h=f\quad mod \quad q h=fmodq
- 预处理:计算 f p fp fp与 f t ( m ? 1 ) ft_{(m-1)} ft(m?1)?
- 步骤: n e w f t = ( ( f t ? T [ s ] × 1 0 m ? 1 m o d q ) × 10 + T [ s + m ] ) m o d q ; newft=((ft-T[s]\times 10^{m-1} mod\quad q)\times10+T[s+m])mod\quad q; newft=((ft?T[s]×10m?1modq)×10+T[s+m])modq;

2.2 伪码实现:
Rabin-Karp-Search(T,P)
q <- a
//a为大于m的素数(n-m个轮换中,每第q次才需要匹配指纹)
c <- 10^(m-1) mod q //运行一个乘以 10 mod q 的循环
fp <- 0; ft <- 0
for i <- 0 to m-1 // 预处理,计算得到fp与ft
fp <- (10*fp + P[i]) mod q
ft <- (10*ft + T[i]) mod q
for s <- 0 to n – m // 匹配
if fp = ft then // 当指纹相同时,逐一比较字符
if P[0..m-1] = T[s..s+m-1] return s
ft <- ((ft – T[s]*c)*10 + T[s+m]) mod q//计算newft
return –1
2.3 算法复杂性分析:
- 预处理: O ( m ) O(m) O(m)
- 外循环: O ( n ? m ) O(n-m) O(n?m)
- 所有内循环: n ? m q × m = O ( n ? m ) \frac{n-m}{q}\times m=O(n-m) qn?m?×m=O(n?m)
- (期望)总时间: O ( n ? m ) O(n-m) O(n?m)
- 最坏运行时间: O ( n m ) O(nm) O(nm),即当每次指纹匹配但匹配字符时总是最后一个无法匹配上。
2.4 实际操作:
- 若字母表中有d个字母,将字母翻译为d进制数字。
- 选择素数q>m。
2.5 缺点分析:
- 没有利用已匹配部分的信息
3. KMP(Knuth-Morris-Pratt )算法
3.1 思路:
-
? 在当前字符失配时,对于已匹配部分,找到匹配部分在模式中的最大前缀同时也是后缀的长度。
即求出 π [ q ] = m a x { k < q ∣ P [ 1.. k ] = P [ q ? k + 1.. q ] } π[q]=max\{k<q|P[1..k]=P[q-k+1..q]\} π[q]=max{k<q∣P[1..k]=P[q?k+1..q]}
-
? 如图所示:


3.2 前缀表:
- 基于该思想,可以预先计算模式 P P P的前缀表:
eg 1:
| P | p | a | p | p | a | r | |
|---|---|---|---|---|---|---|---|
| q | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| p[q] | 0 | 0 | 0 | 1 | 1 | 2 | 0 |
? eg 2:
| P | a | b | a | b | a | c | b | |
|---|---|---|---|---|---|---|---|---|
| q[下标+1] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p[q] | 0 | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
3.3 伪码实现
KMP-Search(T,P)
p <- Compute-Prefix-Table(P) //计算前缀表
q <- 0 // 当前匹配的字符数
for i <- 0 to n-1 // 从左至右扫描文本
while q > 0 and P[q] ≠ T[i] do
//当失配时,匹配字符数赋值为p[q],相当于扫描文本的指针i左移p[q],但实际上文本中每个字符只比较一次
q <- p[q]
if P[q] = T[i] then q <- q + 1 //每匹配一个,则指针均向右扫描一位
if q = m then return i – m + 1 //当匹配的字符数=模式长度,说明实现匹配,返回下标“i-m+1”
return –1
?
- 模式部分:将j直接移动到k位置

3.4 复杂度分析
- 时间复杂度:
O
(
m
+
n
)
O(m+n)
O(m+n)
- 主程序: O ( n ) O(n) O(n)
- 前缀表计算: O ( m ) O(m) O(m)
- 空间复杂度: O ( m ) O(m) O(m), 存储前缀表
4. BMH(Boyer-Moore-Horspool)算法
4.1 BM算法:
-
逆简单算法+启发式规则: O ( m + n ) O(m+n) O(m+n)
-
启发式规则:将失配时文本中对应的字符作为坏字符:
-
坏字符没出现在模式串中,这时可以把模式串移动到坏字符的下一个字符,继续比较:

-
坏字符出现在模式串中,这时可以把模式串第一个出现的坏字符和母串的坏字符对齐。
-
4.2 BMH算法:
-
实现思路:
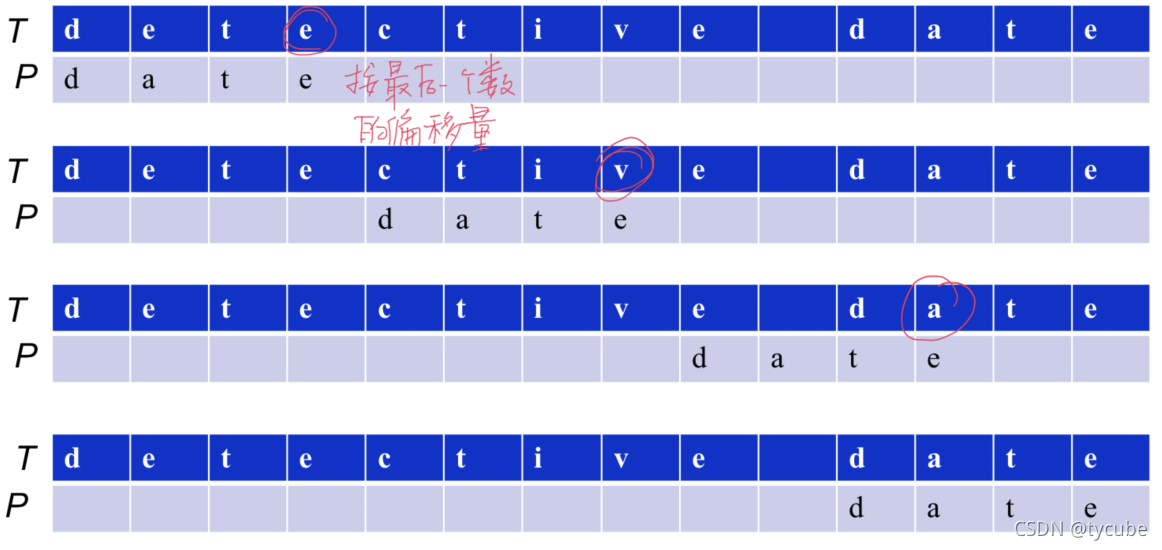
- 仅考虑启发式规则,即利用启发式规则计算偏移表。
- 失配后直接将T[s+m-1]对齐到模式P[0…m-2]中的最右出现。
-
偏移表:
除最后一个元素,其余任何元素偏移量都是从当前位置到结尾需要移动的距离,相同元素取最小偏移量,若最后一个元素只在模式中出现一次,则偏移量为模式长度。
s h i f t [ w ] = { m ? 1 ? m a x { i < m ? 1 ∣ P [ i ] = w } , i f w i s i n P [ 0.. m ? 2 ] m , o t h e r w i s e shift[w]=\begin{cases}m-1-max\{i<m-1|P[i]=w\},if\quad w\quad is\quad in\quad P[0..m-2]\\m,otherwise \end{cases} shift[w]={m?1?max{i<m?1∣P[i]=w},ifwisinP[0..m?2]m,otherwise?
eg:P = “kettle”
? shift[e] =4, shift[l] =1, shift[t] =2, shift[k] =5
-
伪码实现:
BMH-Search(T,P) // 计算模式P偏移表 for c <- 0 to |∑|- 1 shift[c] = m //初始化 for k <- 0 to m - 2 shift[P[k]] = m – 1 - k //计算偏移,从左向右计算,可以计算得到每个元素对应的最小偏移量 // 搜索 s <- 0 //文本部分的开头 while s ≤ n – m do //当还没有比较到末位,即文本中剩余可以进行比较的字符数大于模式长度时。 j <- m – 1 // 逆序比较,故j从m-1开时向前比较。 // check if T[s..s+m–1] = P[0..m–1] while T[s+j] = P[j] do j <- j - 1 if j < 0 return s s <- s + shift[T[s + m – 1]] // 失配时,文本右移T[s+m-1]对应字符的偏移量。 return –1
过程图解:
?
【复杂度分析】:
- 时间复杂度:
- 预处理:$O(m+|∑|)$
- 搜索过程:$O(nm)$
- 总计:$O(mn)$
- 空间复杂度:
- $O(∑)$,偏移表所需空间
9.2 字符串查找数据结构
9.2.1 字符串的ADT
- search(x)、insert(x)、delete(x)
- n个字符串,N个字母,m为需要的操作字符串x的长度,字母表的大小d=|Σ|
9.2.2 字符串的BST
- 使用二分查找树
- 二叉搜索树(Binary Search Tree)是具有二叉树结构,每个节点都有一个可比较的Key , 并且对于任何一个节点而言,它的左边的所有节点的Key都比它的Key小,右边所有节点的Key都比它的Key大。
9.2.3 字符串的Tries(前缀树、字典树)
-
Trie的性质:
- 多路树-每个节点儿子数为含有当前节点为前缀的字符串总数
- 根节点不包含字符
- 每条边标记一个字符
- 每个叶子节点存储字符串,该字符串是从根到叶子所有字符的连接体。
-
Trie的搜索与插入:
-
搜索:自上而下
Trie-Search(t, P[k..m]) //在字典树t中搜索字符串P if t is leaf then return true //当t是一个叶子,即P已经扫描到叶子节点,说明当前叶子存储字符串P //如果扫描到的节点不是字符串P的节点,直接false else if t.child(P[k])=null then return false //否则,扫描当前节点的子节点 else return Trie-Search(t.child(P[k]), P[k+1..m]) -
插入:
Trie-Insert(t, P[k..m]) //在t中插入字符串[k..m] if t is not leaf then //当确认P不在t中,执行插入操作 if t.child(P[k])=null then //如果当前扫描到的字符树节点不属于t的子节点,直接创建新节点 创建 t 的新孩子和从该孩子开始并存储在 P[k..m] 的“分支” 中 //否则插入P[k+1..m]进入t的以P[k]开始的子树中 else Trie-Insert(t.child(P[k]), P[k+1..m]) -
删除:自底向上,删除直到当前节点含有其他子节点(包括叶子节点)
-
-
Trie的分析:
- 最坏情况:$O(N)
- { 搜 索 ? O ( d m ) 插 入 ? O ( m l g d ) 删 除 ? O ( m ) \begin{cases}搜索-O(dm)\\插入-O(mlgd)\\删除-O(m)\end{cases} ??????搜索?O(dm)插入?O(mlgd)删除?O(m)?,m为字符串的长度
9.2.4 紧缩Trie
-
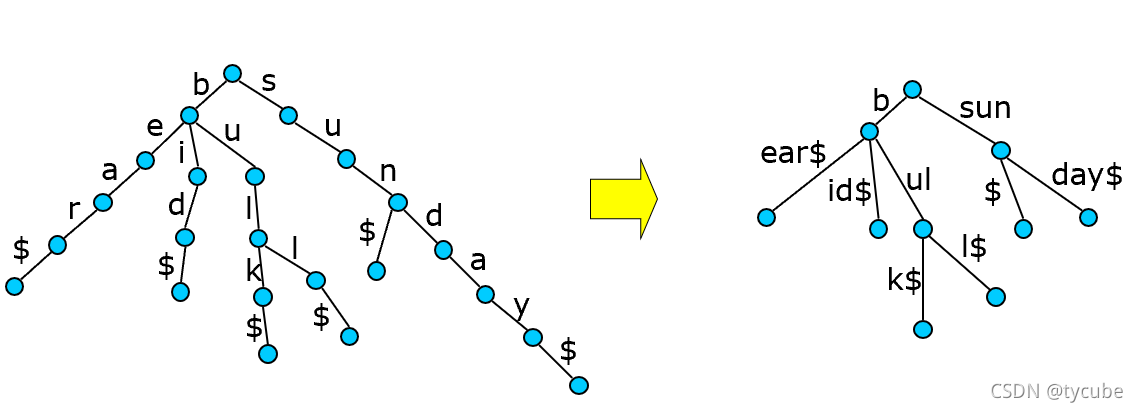
-
紧缩Tries II
- 数组存放字符串,trie中的边存放字符在数组中的位置。
- 数组存放字符串,trie中的边存放字符在数组中的位置。
-
Patricia trie
-
边标记改为**(字符串开头, 字符串长度)**,将文本的比较推迟到最后。
-

-
伪码:(单词前缀查询P[0…m-1])
Patricia-Search(t, P, k) if t is leaf then //如果t是叶子节点,将t在列表中的第一个索引赋值给j j <- the first index in the t.list if T[j..j+m-1] = P[0..m-1] then //若从j到j+m-1也能匹配上,返回对应的t的列表 return t.list // 匹配成功 else if there is a child-edge (P[k],s) then //如果t中有一条P[k]为开头,长度为s的字符边 if k + s < m then //当加入该字符串后还没有扫描到P[m-1] return Patricia-Search(t.child(P[k]), P, k+s) //从t树的P[k]节点查找其子树中对应P[k+s,...m-1]的部分 else 转到任意t的叶子, 进行第4行的操作 if it is true, 返回 t 的所有后代叶子的列表 otherwise return nil else return null // nothing is found
-
-
9.2.5 文本搜索问题
- 后缀树
- Pat树

