一、2-3-4树
1.多叉树
二叉树中,每个节点有一个数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点。2-3-4树就是多叉树,它的每个节点最多有四个子节点和三个数据项。
2.特点:
- 有一个数据项的节点总是有两个子节点
- 有两个数据项的节点总是有三个子节点
- 有三个数据项的节点重是有四个子节点
- 所有叶子结点都拥有相同的深度
- 每个节点的key从左到右保持了从小到大的顺序,两个key之间的子树中所有的key一定大于它的父节点的左key,小于父节点的右key
.叶子结点为null
.每一颗2-3-4树对应一棵的红黑树结构
3.三种节点示意图
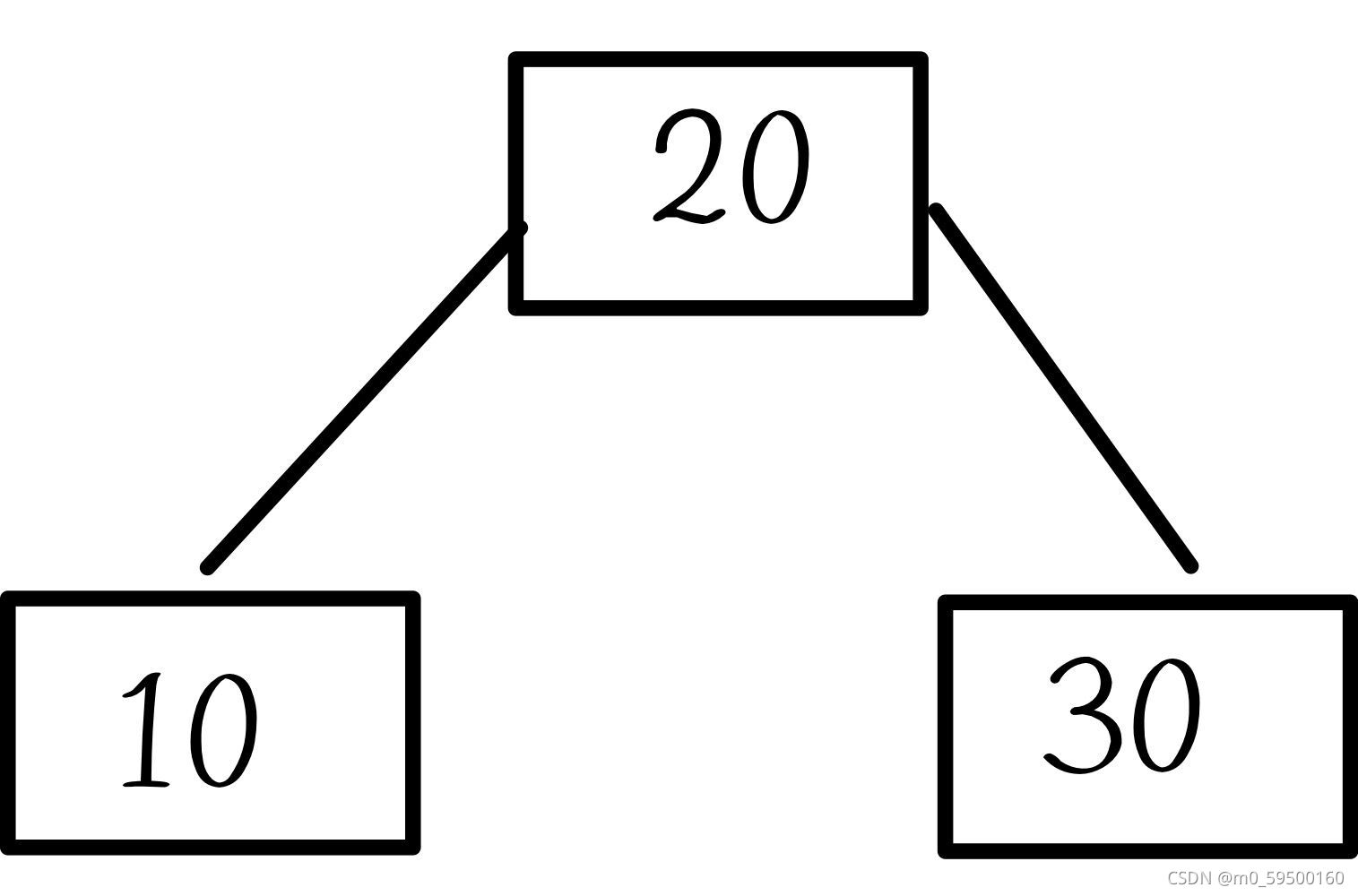
- 2-节点:有两个子树的节点
??????????????????????????????????????????????????
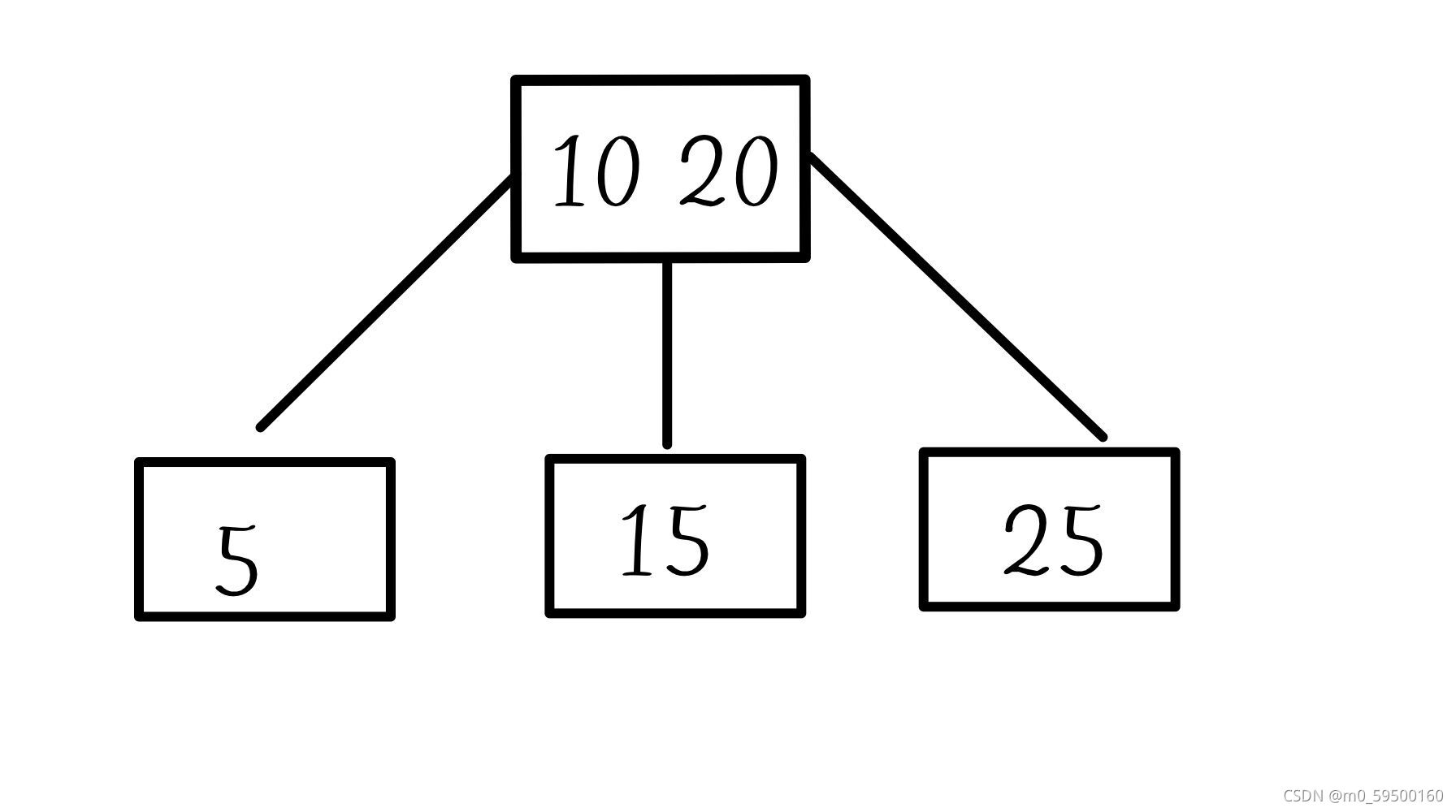
- 3-节点:有三个子树的节点
????????????????????????????????????????????????????????????????????????????
- 4-节点:有四个子树的节点
??????????????????????????????????????????????????????????????????????????????????? ? ? ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? ??
二、红黑树
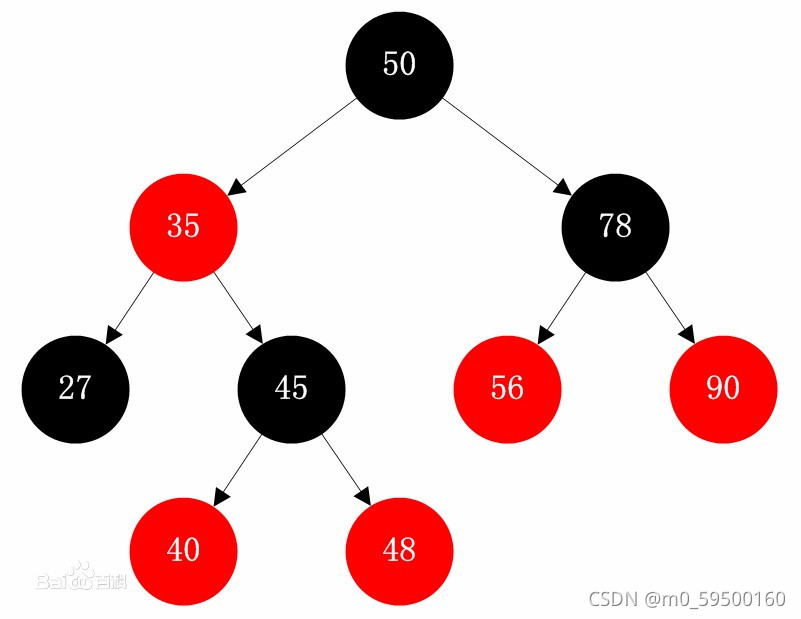
1.红黑树特性
- (1) 每个节点或者是黑色,或者是红色。
- (2) 根节点是黑色。
- (3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!
- (4) 如果一个节点是红色的,则它的子节点必须是黑色的。
- (5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
例如:
2.通过2-3-4树构建红黑树原理?
- 新插入的结点颜色为红色,这样才可能不会对红黑树的高度产生影响。
- 结点对应红黑树中的单个黑色结点,插入时直接成功(对应2-结点升元)。°3结点对应红黑树中的黑+红子树,插入后将其修复成红+黑+红子树(对应3结点升元)
- 结点对应红黑树中的红+黑+红子树,插入后将其修复成红色祖父+黑色父叔+红色孩子子树,然后再把祖父结点当成新插入的红色结点递归向上层修复,直至修复成功或遇到root结点
3.注意点
- 特性(3)中的叶子节点,是只为空(null)的节点。
- 特性(5),确保没有一条路径会比其他路径长出两倍。因而,红黑树是相对是接近平衡的二叉树。