开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 入门二叉树-一起来递归【上】 -> 正文阅读

[数据结构与算法]入门二叉树-一起来递归【上】

1. 单值二叉树

本题来源于leetcode 965. 单值二叉树

1.1 题目描述

提示

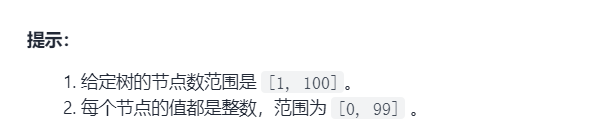
1.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isUnivalTree(struct TreeNode* root){

}

1.2 大致框架

1.2.1 思路与想法

二叉树的题目化为递归做，分析一颗树还是看它的root与leftchild和rightchild，只要看

三个节点的值是否相等不相等，相等就继续往下走
在走的时候要保证return false的情况的条件，这个容易写错

1.2.2 具体步骤

我们之前说的要看三个节点相不相等怎么来进行判断？

实际上只要证明leftchild==root和rightchild==root就可以证明这三个之间是不是互相都相等了，从而可以递归到更深层的子树都是相等的

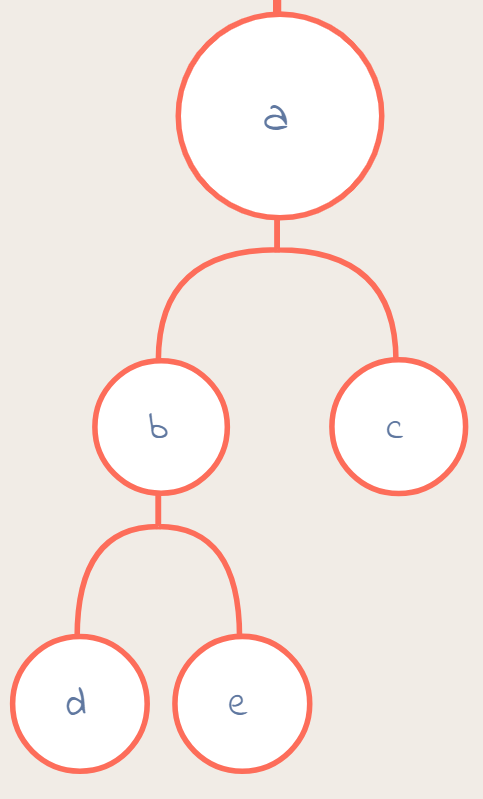
只要a=b=c,b=d=e,那么a=d=e，等号的传递性，也在于题目的特殊，所以可以解决起来很简单
return false 的条件

如果只判断和root是否一样的话，是不够的，因为可能出现左孩子或这右孩子是空的，如果对空不排除的话，会算成返回false，因为NULL！=root->val,然而总要有空的情况出现，显然打不倒题目的要求，所以要加一个排空的条件

1.3 整体实现

bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
{
    return true;
}
if(root->left&&root->left->val!=root->val)//保证左值不空和左儿子不等于父亲
{
    return false;
}
if(root->right&&root->right->val!=root->val)
{
    return false;
}
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

2.二叉树的最大深度

本题目来源于 104. 二叉树的最大深度

2.1 题目描述

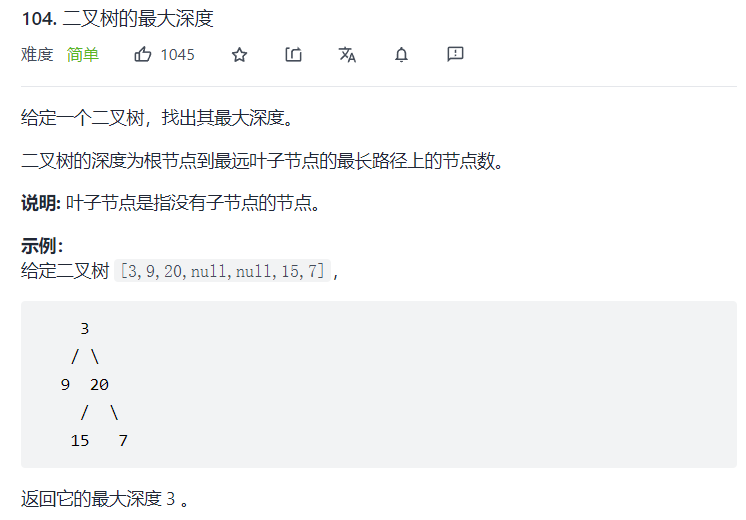
2.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


int maxDepth(struct TreeNode* root){

}

2.2 大致框架

2.2.1 思路与想法

关键在于如何求一棵树的深度

分析书的模型可以想到一棵树的深度就是左子树和右子树的深度较大的那棵+1，由此又是递归产生了

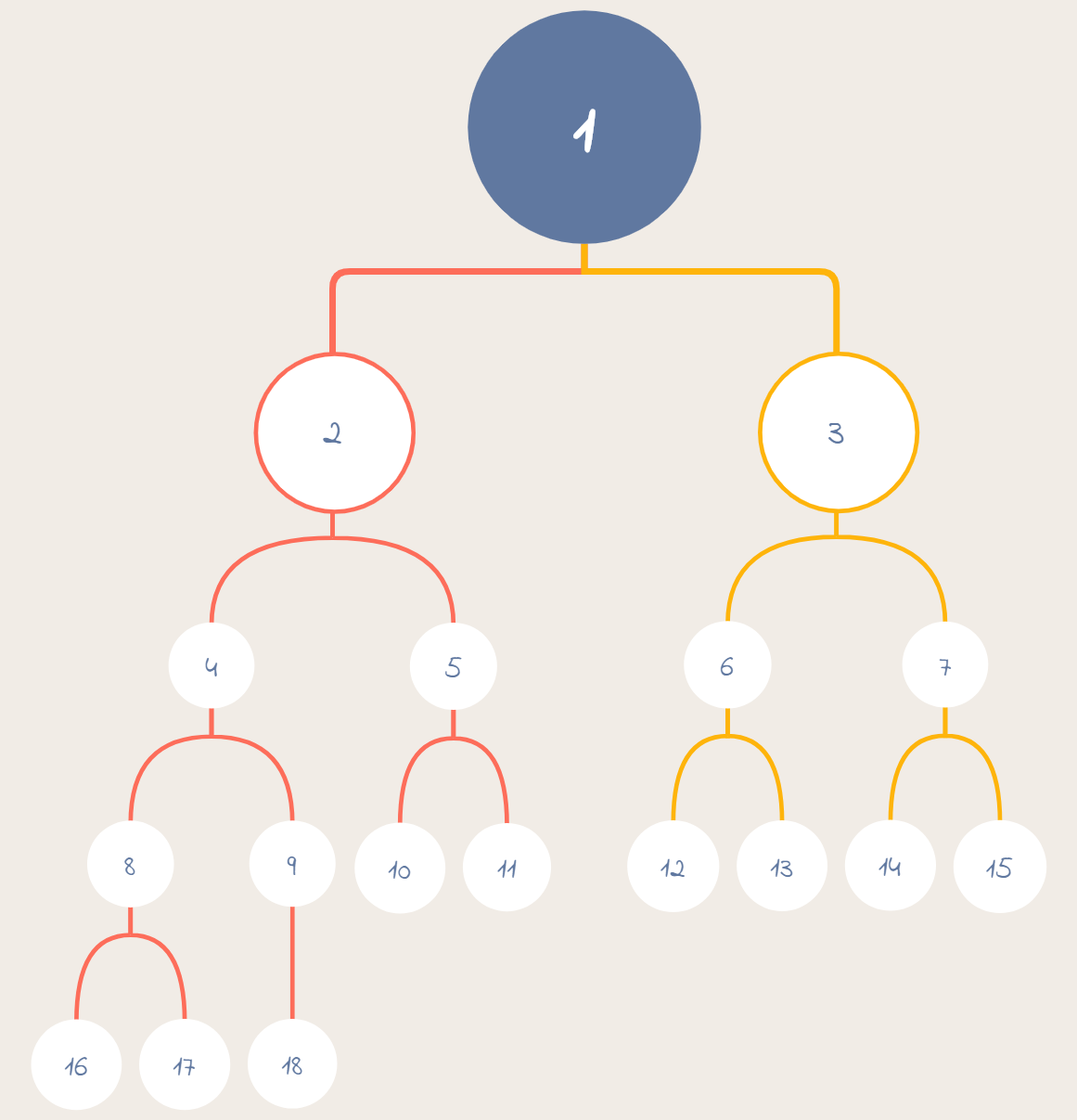
2.2.2 具体步骤

int maxDepth(struct TreeNode* root){
if(root==NULL)
{
    return 0;
}
return maxDepth(root->left)>maxDepth(root->right)?
maxDepth(root->left)+1:maxDepth(root->right)+1;
}

但是提示超出时间限制

一般倘若看上去是那么给了那么多组数据的话，超出了时间限制，说明题目这里堆时间复杂度给出了更高的要求

这里慢的原因是因为用三目操作符时相当于要return+1节点是，把左子树或者右子树深度又算了一遍，凭空增加了很多的时间，纯属浪费，所以这样不好，需要改进

只需要把求出来的值保存在变量里面就可以防止重复计算了

2.3 整体实现

int maxDepth(struct TreeNode* root){
if(root==NULL)
{
    return 0;
}
int leftDepth=maxDepth(root->left);
int rightDepth=maxDepth(root->right);
return leftDepth>rightDepth?leftDepth+1:rightDepth+1;
}

补充:

还有一种方法可以解决
int maxDepth(struct TreeNode* root){
if(root==NULL)
{
    return 0;
}
return fmax(maxDepth(root->left),maxDepth(root->right))+1;
}
fmax在这里没有重复调用，因为这里保存到形参里面去计算，没有重复计算

3.二叉树的前序遍历

本题目来源于leetcode 144. 二叉树的前序遍历

3.1 题目描述

非递归的方法用c++会简单一点，之后学习c++后会使用c++实现

3.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* preorderTraversal(struct TreeNode* root, int* returnSize){

}

3.2 大致框架

3.2.1 思路与想法

由于c语言的数组不想c++一样有vector，所以必须要malloc，但是malloc多少大小还是不清楚，所以为了避免增容问题，获取一下TreeSize，然后用_preorder实现前序遍历，最后通过返回值传给接口，解决问题，返回要求的值

3.2.2 具体步骤

先实现一下TreeSize

int TreeSize(struct TreeNode*root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }

正常走一遍前序遍历，放入数组

 void _preorder(struct TreeNode* root, int* arr ,int i)
 {
     if(root==NULL)
     return ;
     arr[i++]=root->val;
     _preorder(root->left,arr,i);
     _preorder(root->right,arr,i);
 }

最后把主函数完善好就可以了

但是出现了随机值

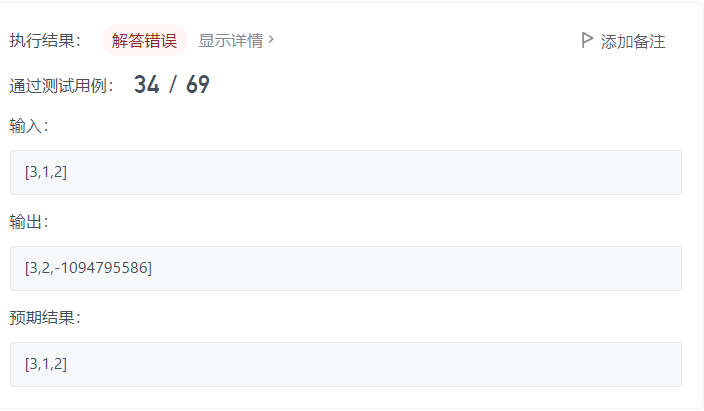
其实原因还是形参的问题
_preorder(root->left,arr,i);
这样的一行传入的i是形参，形参只是一份临时拷贝，不能改变，所以i没有++，要改成传地址
 void _preorder(struct TreeNode* root, int* arr ,int pi)
 {
     if(root==NULL)
     return ;
     arr[(*pi)++]=root->val;
     _preorder(root->left,arr,pi);
     _preorder(root->right,arr,pi);
 }

3.3 整体实现

 int TreeSize(struct TreeNode*root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }
 void _preorder(struct TreeNode* root, int* arr ,int *pi)
 {
     if(root==NULL)
     return ;
     arr[(*pi)++]=root->val;
     _preorder(root->left,arr,pi);
     _preorder(root->right,arr,pi);
 }

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize=TreeSize(root);
    int *arr=(int*)malloc(sizeof(int)*(*returnSize));
int i=0;
_preorder(root,arr,&i);
return arr;
}

4.相同的树

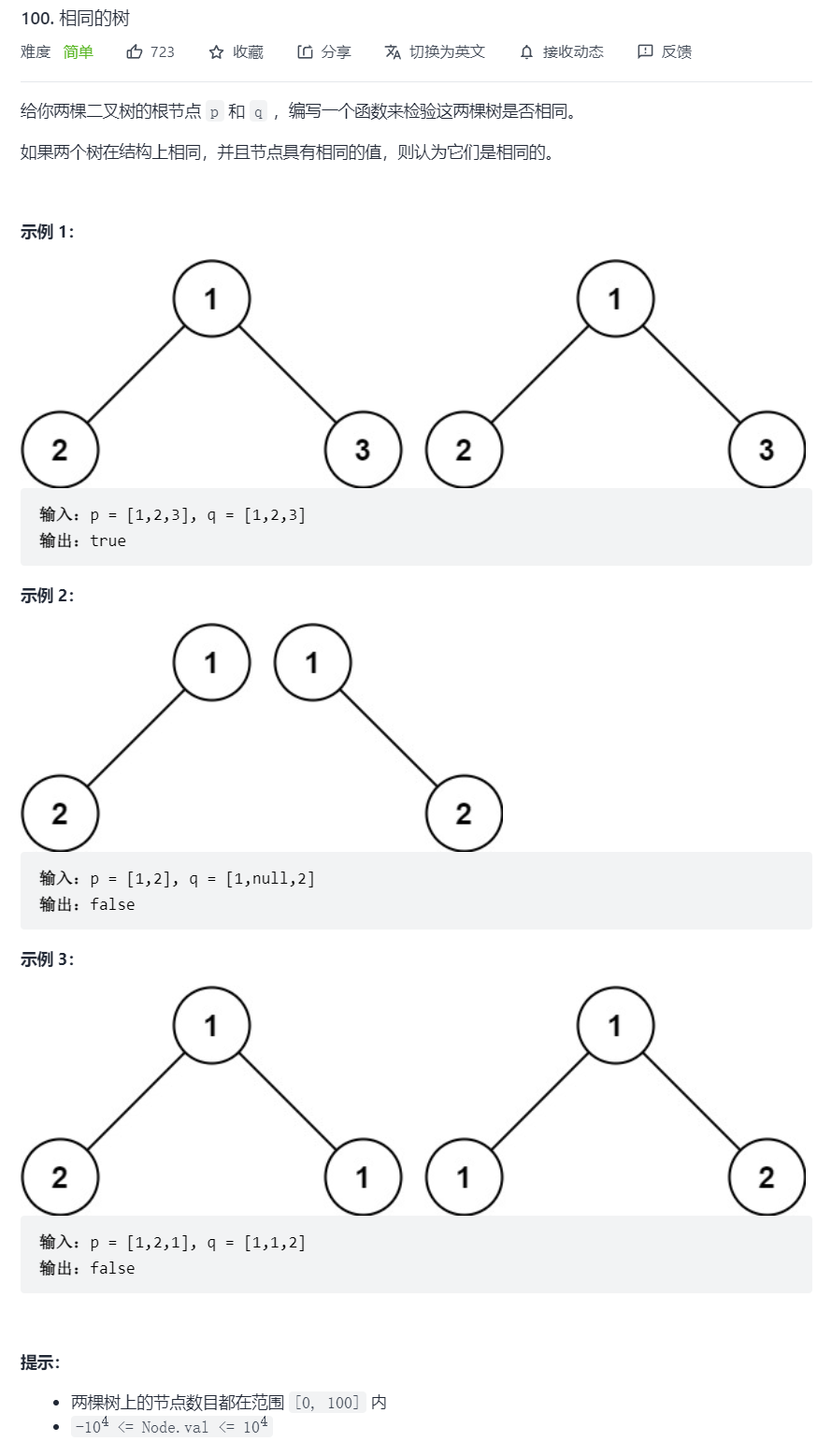
本题目来源于leetcode 100. 相同的树

4.1 题目描述

4.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isSameTree(struct TreeNode* p, struct TreeNode* q){

}

4.2 大致框架

4.2.1 思路与想法

列多种情况排除

4.2.2 具体步骤

双空情况，true
一个空一个不空，false
值不一样，false
往子树走

4.3 整体实现

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
	if (p == NULL && q == NULL)
	{
		return true;
	}
	if (p == NULL || q == NULL)
	{
		return false;
	}
	if (p->val != q->val)
	{
		return false;
	}
	return
		isSameTree(p->left, q->left) &&
		isSameTree(p->right, q->right);
}

5.翻转二叉树

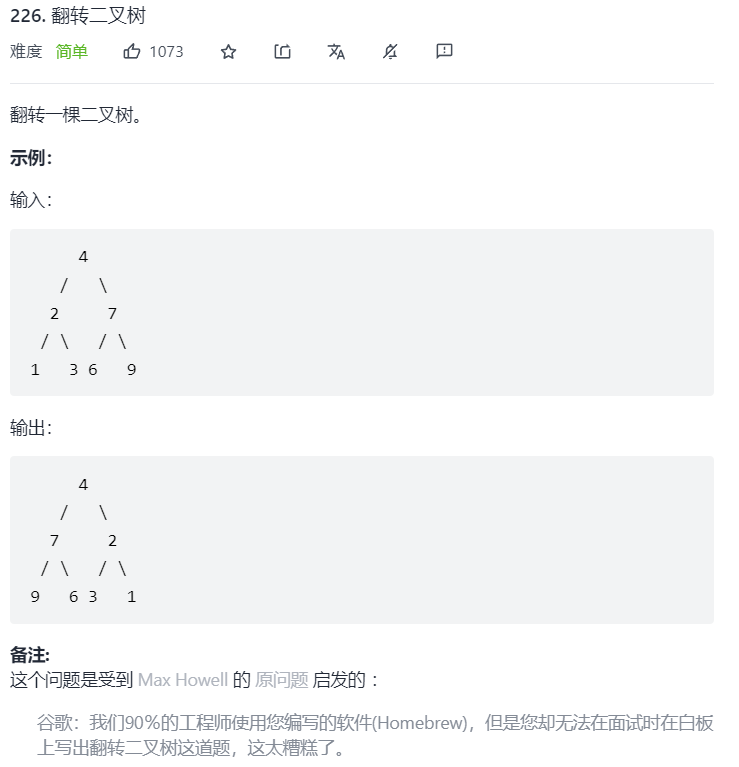
本题目来自leetcode 226. 翻转二叉树

5.1 题目描述

5.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* invertTree(struct TreeNode* root){

}

5.2 大致框架

5.2.1 思路和想法

由于要求的输出的左右子树的位置跟输入正好是相反的，我们可以递归的交换左右子树来完成这道题。

时间复杂度： O(n)
空间复杂度： O(h)

5.2.2 具体步骤

终止条件：当前节点为 NULL 时返回
递归条件：交换当前节点的左右节点，再递归的交换当前节点的左节点，递归的交换当前节点的右节点
利用tmp实现交换

5.3 整体实现

struct TreeNode* invertTree(struct TreeNode* root){
if(root==NULL)
{
    return NULL;
}
 struct TreeNode*tmp=root->left;
    root->left=root->right;
    root->right=tmp;
     invertTree(root->left);
    invertTree(root->right);
    return root;
}