一、鲸鱼优化算法优化支持向量机简介
1 改进的二进制 WOA
为了改善 WOA 算法在搜索过程中的收敛速度慢和陷入局部最优的缺点,提出一种改进二进制鲸鱼优化算法( IBWOA) 。 ( 1) 非线性收敛因子策略。为了更好地协调算法的全局搜索和局部搜索,本文提出一种新的非线性收敛因子策略,
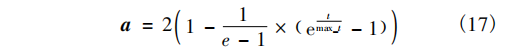
2) 更新机制中引入粒子群优化策略。在 WOA算法的更新机制中,为了降低 WOA 算法陷入局部最优解的概率,本文采用粒子群优化策略对种群进行多样性操作。通过粒子群中的 ω 权重使算法快速跳出局部极值,使得种群更具有多样性。
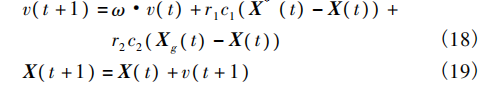
式中: Xg 为个体最优位置; ω 是速度惯性权重; c1,c2表示学习因子; v t ( ) + 1 是 t + 1 次迭代时第 i 个粒子的速度。
为了实现鲸鱼个体位置在 0 和 1 之间的更新转换,本文采用的二进制更新转换函数[9]如下:
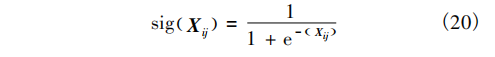

2 IBWOA-SVM 方法
SVM 的分类性能关键在于参数的设置,只有选择合适的 SVM 参数,才能得到高维空间的最优分类模型。关于对 SVM 参数的选取,目前研究最热的是采用智能优化算法来优化 SVM 参数方法,比如: 粒子群、蚁群和人工蜂群等。但是,这些智能算法存在着收敛速
度慢以及容易陷入局部最优等不足。因此,本文在前期工作的基础上,提出一种 IBWOA-SVM 方法,用来优化 SVM 的两个重要参数( 惩罚参数 C 和核参数 g) ,进而提高分类的准确率。
2.1流程图
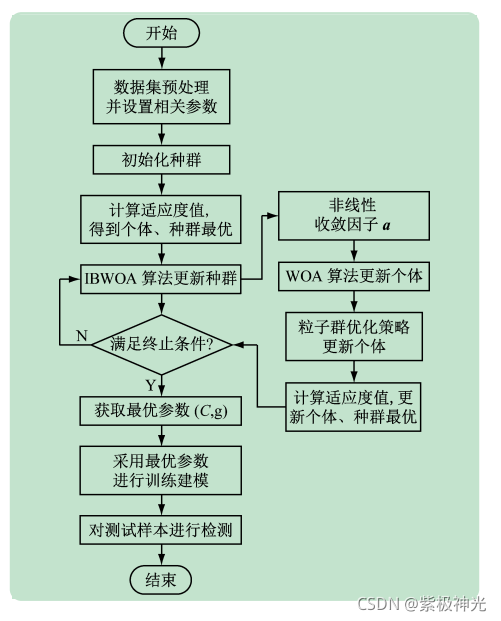
图 1 所示为 IBWOA-SVM 方法的流程图。
IBWOA-SVM 方法的具体优化步骤如下:
( 1) 数据预处理,设置种群数量 n、最大迭代次数max_t、设定 C 和 g 的取值范围。
( 2) 将 SVM 的参数设定为每个鲸鱼个体,初始化种群。
( 3) 由 K 折交叉验证法计算每个鲸鱼个体的适应度值,记录当前个体及种群最优值。
( 4) 采用改进后的 IBWOA 算法对种群个体进行位置更新
5) 再次计算适应度值,通过适应度值的比较,更
新个体最优解及种群最优解,并获取新的种群。 ( 6) 判断算法是否满足终止条件; 若满足,则转到
( 7) ; 否则,转到( 4) 。 ( 7) 获取最优参数( C,g) 。 ( 8) 采用最优参数对训练样本进行训练建模。 ( 9) 采用建好的模型对测试样本进行检测。 ( 10) 输出最优参数( C,g) 及分类准确率。
2.2 伪代码
算法 1 IBWOA-SVM。
输入: 最大迭代次数 max_t,种群数 n,C 和 g 的取
值区间。
输出: 最优参数及分类准确率。
1. 初始化种群。
2. 计算个体的适应度值,得到个体最优及种群
最优。
3. WHILE 是否满足终止条件。
4. 更新 a,l,A,C,其中 a 为改进的非线性收敛因子。
5. FOR。
6. WOA 算法更新当前种群。
7. 采用粒子群优化策略更新当前种群。
8. END FOR。
9. 再次计算个体的适应度值,更新个体最优及种
群最优。
10. 采用最优参数( C,g) 对训练样本进行训练
建模。
11. 采用建好的模型对测试样本进行检测。
12. END WHILE。
返回最优参数( C,g) 及分类准确率。如算法 1 的伪代码所示,在 IBWOA-SVM 的搜索
过程中,对参数 a 采用非线性收敛因子策略,来协调算法的全局搜索和局部搜索; 在更新机制中引入粒子群优化策略,来保证种群的多样性,进而提高网络入侵的分类性能。
二、部分源代码
data=xlsread('数据.xlsx','Sheet1','A1:N178'); %使用xlsread函数读取EXCEL中对应范围的数据即可
%输入输出数据
input=data(:,1:end-1); %data的第一列-倒数第二列为特征指标
output_labels=data(:,end); %data的最后面一列为标签类型
三、运行结果
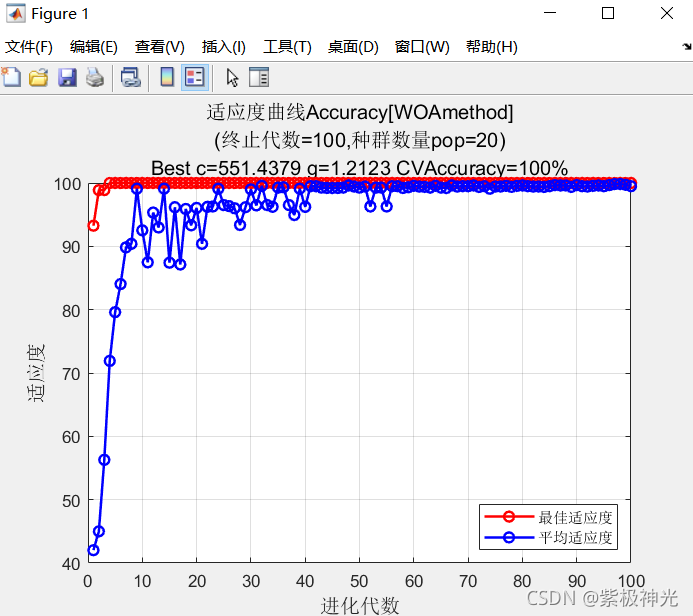
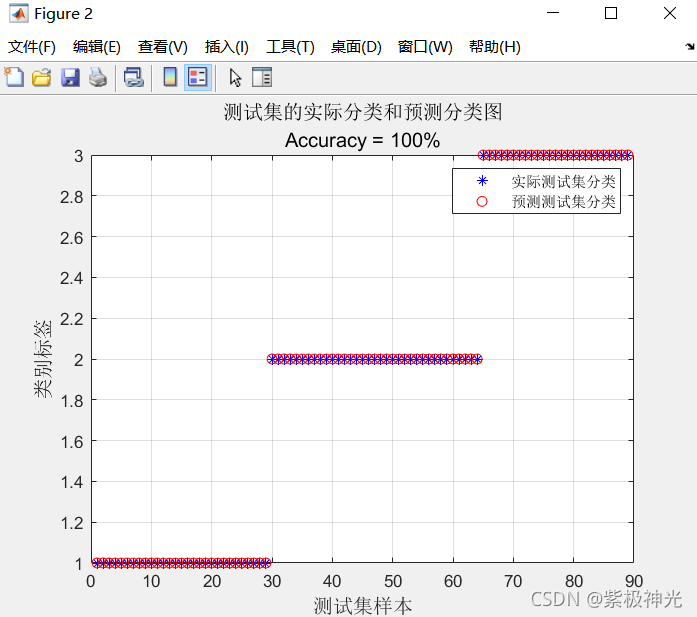
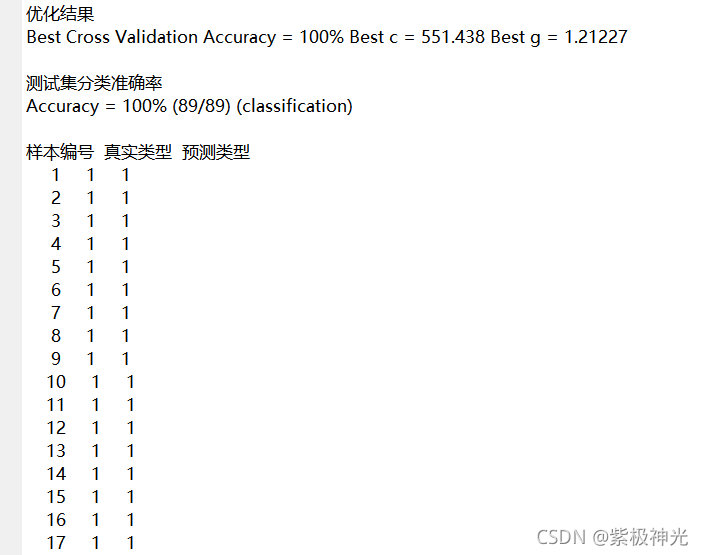
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社,2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社,2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社,2018.
[6]徐慧,付迎春,付朝川,叶志伟.改进WOA算法优化SVM的网络入侵检测[J].实验室研究与探索. 2019,38(08)