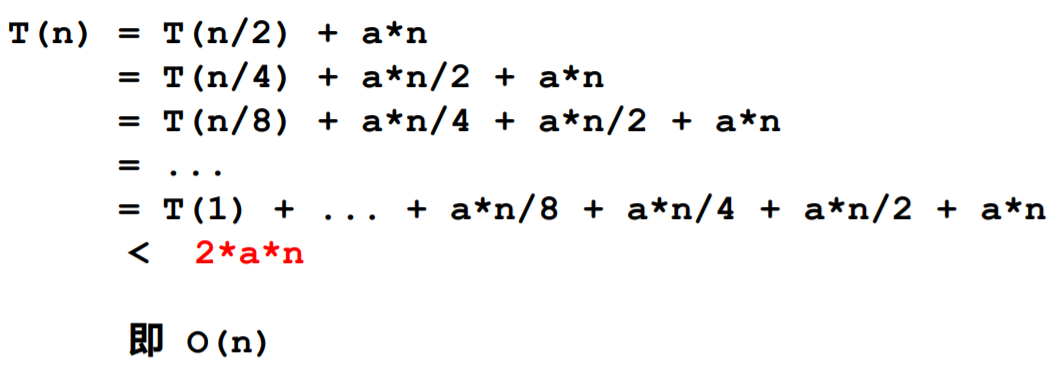[数据结构与算法]算法分析与设计「四」分治算法

一、什么是分治算法

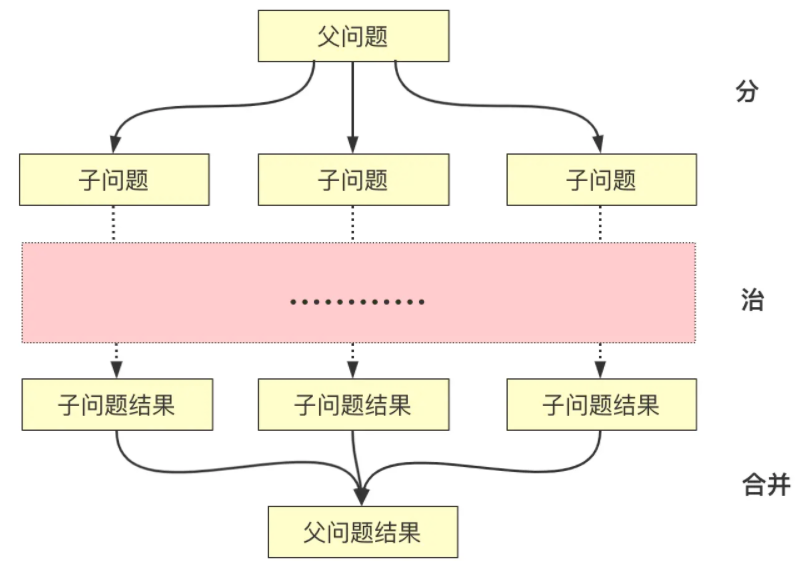
分治算法的基本思想是将一个规模为 N 的问题分解为 K 个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。

一般思路

• 分解：将要解决的问题划分成若干规模较小的同类问题；
• 求解： 当子问题划分得足够小时，用较简单的方法解决；
• 合并： 按原问题的要求，将子问题的解逐层合并构成原问题的解。
  

例如下面的找出伪币问题，就是一个典型的分治法应用：

问题描述：16 硬币，有可能有1枚假币，假币比真币轻。有一架天平，用最少称量次数确定有没有假币，若有的话，假币是哪一枚。

分治解决：将对 16 个硬币的搜索问题，转为对两组 8 个硬币搜索的问题。在 8 - 8 个硬币进行称量，找出较轻的；然后 4 - 4 个硬币称量，找出较轻的；之后 2 - 2 个称量，找出较轻的；最后 1 - 1 个称量，找出较轻的即为假币。
?

二、分治的典型应用

应用一：归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。其实现排序时的时间复杂度为 $O(nlogn)$ 。

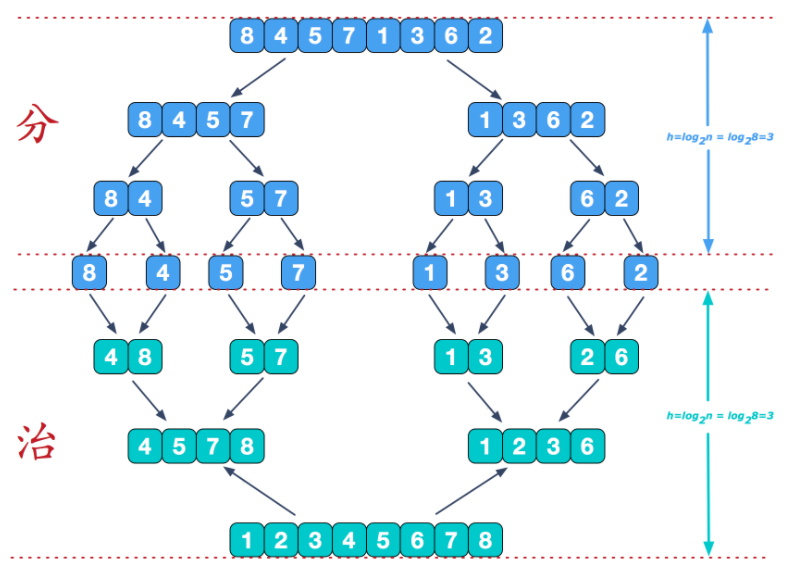
思路分析：数组排序任务可以如下完成：① 把前一半排序 ② 把后一半排序 ③ 把两半归并到一个新的有序数组，然后再拷贝回原数组，排序完成。参考下图：

代码实现：

#include <iostream>
using namespace std;

int a[8] = {8, 4, 5, 7, 1, 3, 6, 2};
int b[8]; // 用于存放中间结果

// 将两个半有序数组有序地排到 tmp[] 中，之后拷贝给 a[]。复杂度 O(n)
void Merge(int a[], int s, int m, int e, int tmp[])
{
    int pb = 0;
    int p1 = s, p2 = m + 1;
    while (p1 <= m && p2 <= e)
    {
        if (a[p1] < a[p2])
            tmp[pb++] = a[p1++];
        else
            tmp[pb++] = a[p2++];
    }
    while (p1 <= m)
        tmp[pb++] = a[p1++];
    while (p2 <= e)
        tmp[pb++] = a[p2++];

    // 拷贝回原数组
    for (int i = 0; i < e - s + 1; ++i)
        a[s + i] = tmp[i];
}

// 利用递归思想
void MergeSort(int a[], int s, int e, int tmp[])
{
    if (s < e)
    {
        int m = s + (e - s) / 2;     // 中点
        MergeSort(a, s, m, tmp);     // 前段排序
        MergeSort(a, m + 1, e, tmp); // 后段排序
        Merge(a, s, m, e, tmp);      // 归并
    }
}

int main()
{
    int size = sizeof(a) / sizeof(int);
    MergeSort(a, 0, size - 1, b);
    for (int i = 0; i < size; ++i)
        cout << a[i] << ",";
    cout << endl;
    return 0;
}

归并排序时间复杂度分析：

?

应用二：快速排序

基本思想：

1. 在待排序数组中首先选取一个记录作为基准（pivotkey），通常选第一个元素。
2. 经过一趟排序，将小于基准的元素放在左侧，大于基准的元素放在右侧，基准元素放置在分解处。这样，待排序数组就分成了两个子表。（需要时间 $O(n)$)
3. 递归地将左侧和右侧的两个子表进行排序，直至每个子表只有一个元素。

具体步骤：

1. 暂时指定第一个记录为基准，同时附设两个指针 i，j 分别指向数组的第一个元素和最后一个元素。
   
2. 从表的最右侧位置依次向左搜索，找到小于基准的元素，与基准元素进行交换；如果没有找到，则指针左移。
   
   
3. 再从数组最左侧位置开始，找到大于基准的元素，与基准进行交换；若没找到，则指针右移。
   
   
   
   
4. 重复步骤 2 和 3，直至指针 i 和 j 相等。这样第一趟递归排序就完成了，原表被分为了左右两个子表。下面只需递归操作即可。
   
   

代码实现：

#include <iostream>
using namespace std;

void swap(int &a, int &b)
{
    int tmp = a;
    a = b;
    b = tmp;
}

void QuickSort(int a[], int s, int e)
{
    if (s >= e)
        return;
    int k = a[s];     // k 为基准
    int i = s, j = e; // 左右指针
    // 下面进行一趟排序
    while (i != j)
    {
        while (j > i && a[j] >= k)
            --j;
        swap(a[i], a[j]);
        while (i < j && a[i] <= k)
            ++i;
        swap(a[i], a[j]);
    } // 此时 a[i] = k
    QuickSort(a, s, i - 1);
    QuickSort(a, i + 1, e);
}

int a[] = {2, 1, 3, 7, 12, 11, 8, 9};

int main()
{
    int size = sizeof(a) / sizeof(int);
    QuickSort(a, 0, size - 1);
    for (int i = 0; i < size; ++i)
        cout << a[i] << ' ';
    cout << endl;
    return 0;
}

注意：有个小问题，在实现 swap 交换两个数时，刚开始用到了异或运算 a^=b; b^=a; a^=b; ，发现输出了好多 0。这时因为 i 最终等于 j，这时两个要交换的数相等，导致 i ^ j = 0 。

复杂度分析：

快速排序的最坏时间复杂度是 $O(n2)$，比如说顺序数列的快排。但它的平均时间复杂度是 $O(nlogn)$，且 $O(nlogn)$ 记号中隐含的常数因子很小，比复杂度稳定等于 $O(nlogn)$ 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。
?

应用三：输出前 m 大的数

问题描述：给定一个数组包括 n 个元素，统计前 m 大的数并且把这 m 个数从大到小输出。

输入：第一行包含一个整数 n，表示数组的大小（n < 100000）。第二行包含 n个整数，表示数组的元素，整数之间以一个空格分开。每个整数的绝对值不超过100000000。第三行包含一个整数 m（m < n）。

输出：从大到小输出前m大的数，每个数一行。

解题思路：当然，你可以选择先排序后再进行输出，这时时间复杂度 $O(nlogn)$。但其实我们可以选择一种时间复杂度更小的解法：把前 m 大的都弄到数组最右边，复杂度 $O(n)$ 。然后对这最右边 m 个元素排序再输出， 复杂度 $O(logn)$ 。总的时间复杂度为 $O(n+mlogm)$。当 m << n 时，这种算法时间复杂度相当于 $O(n)$，优势就比较明显了。

将前 m 大的都弄到数组最右边的时间为什么为 $O(n)$ ？

// 输入样例
5
5 2 11 3 12
3
// 输出样例
5
11
12

代码实现：

#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 100005

int a[MAXN];
int n, m;

void swap(int &a, int &b)
{
    int tmp = a;
    a = b;
    b = tmp;
}

// 利用分治思想 ———— 先将前 m 大的数移至右边，再对这 m 个数排序
void arrangeRight(int a[], int s, int e, int k)
{
    if (s >= e)
        return;
    if (k == e - s + 1)
        return;
    int i = s, j = e;
    int key = a[s];
    // 基准元素归位，使得左侧小于基准元素，右侧大于基准元素
    while (i != j)
    {
        while (i < j && a[j] >= key)
            --j;
        swap(a[i], a[j]);
        while (i < j && a[i] <= key)
            ++i;
        swap(a[i], a[j]);
    }
    // 边界条件及递归方式
    if (k == e - i + 1)
        return;
    else if (k < e - i + 1)
        arrangeRight(a, i + 1, e, k);
    else
        arrangeRight(a, s, i - 1, k - e + i - 1);
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; ++i)
        cin >> a[i];
    cin >> m;
    // 前 m 大的数弄到右边
    arrangeRight(a, 0, n - 1, m);
    // 再对这 m 个数排序，sort 类似快排，n*log(n)。
    sort(a + n - m, a + n);
    while (m--)
        cout << a[--n] << endl;
    return 0;
}

?

应用四：求排列的逆序数

问题描述：

解题思路：

当然，你可以采取枚举方式，对每一个元素都遍历，复杂度 $O(n^2)$ 会超时，因此这里暂且不提此解法。

下面来看分治算法解决此问题，其复杂度为 $O(nlogn)$

1. 将数组分成两半，分别求出左半边的逆序数和右半边的逆序数；
2. 再算有多少逆序是由左半边取一个数和右半边取一个数构成的。（要求 $O(n)$ 实现）

如何用 $O(n)$ 时间实现第二步呢 ？关键就是：左半边和右半边都是排好序的。比如，都是从大到小排序的。这样，左右半边只需要从头到尾各扫一遍，就可以找出由两边各取一个数构成的逆序个数。

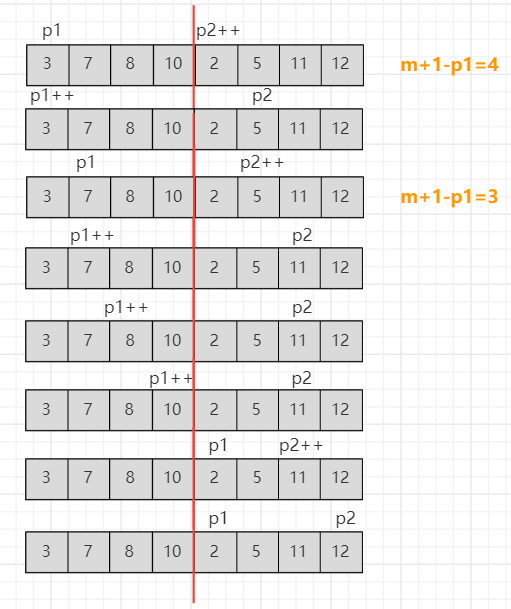
其实总结而言，此问题解法可以由归并排序改进所得，只需加上计算逆序的步骤即可。

代码实现：

#include <iostream>
using namespace std;

int a[8] = {3, 7, 8, 10, 2, 5, 11, 12};
int b[8];      // 用于存放中间结果
int count = 0; // 记录逆序数

// 归并有序序列，并计算逆序数个数
void MergeAndCountNum(int a[], int s, int m, int e, int tmp[])
{
    int pb = 0;
    int p1 = s, p2 = m + 1;
    while (p1 <= m && p2 <= e)
    {
        if (a[p1] < a[p2])
            tmp[pb++] = a[p1++];
        else
        {
            tmp[pb++] = a[p2++];
            // 当出现一个逆序时，其后 m+1-p1 个数都是逆序
            count += m + 1 - p1;
        }
    }
    while (p1 <= m)
        tmp[pb++] = a[p1++];
    while (p2 <= e)
        tmp[pb++] = a[p2++];
    for (int i = 0; i < e - s + 1; ++i)
        a[s + i] = tmp[i];
}

// 利用递归思想
void MergeSort(int a[], int s, int e, int tmp[])
{
    if (s < e)
    {
        int m = s + (e - s) / 2;           // 中点
        MergeSort(a, s, m, tmp);           // 前段排序
        MergeSort(a, m + 1, e, tmp);       // 后段排序
        MergeAndCountNum(a, s, m, e, tmp); // 归并同时计算逆序数
    }
}

int main()
{
    int size = sizeof(a) / sizeof(int);
    MergeSort(a, 0, size - 1, b);
    cout << count;
    return 0;
}