文章目录
前言
多图预警!!!
搜索的问题一般分为两种,一种是在逐层建立起来的二叉树中搜索某一个值的问题,另一种就是搜索最短路径的问题。
基本的搜索策略
广度优先搜索
广度优先搜索的步骤
广度优先搜索与深度优先搜索都是对含有要搜索值的二叉树的搜索。
1.构造根组成的队列Q
2.如果队列第一个元素是要查找的元素则搜索停止。
3.如果队头元素x不是目标节点则从Q中删除,并把所有的子节点加入Q的队尾。并进行循环。
4.如果队列为空则失败。
Puzzle问题
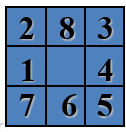
输入:具有八个小方格的魔方。
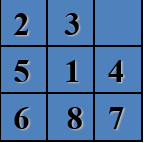
输出:经过移动使得魔方呈现以下状态。
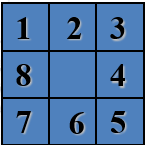
可以转换成树的搜索问题:
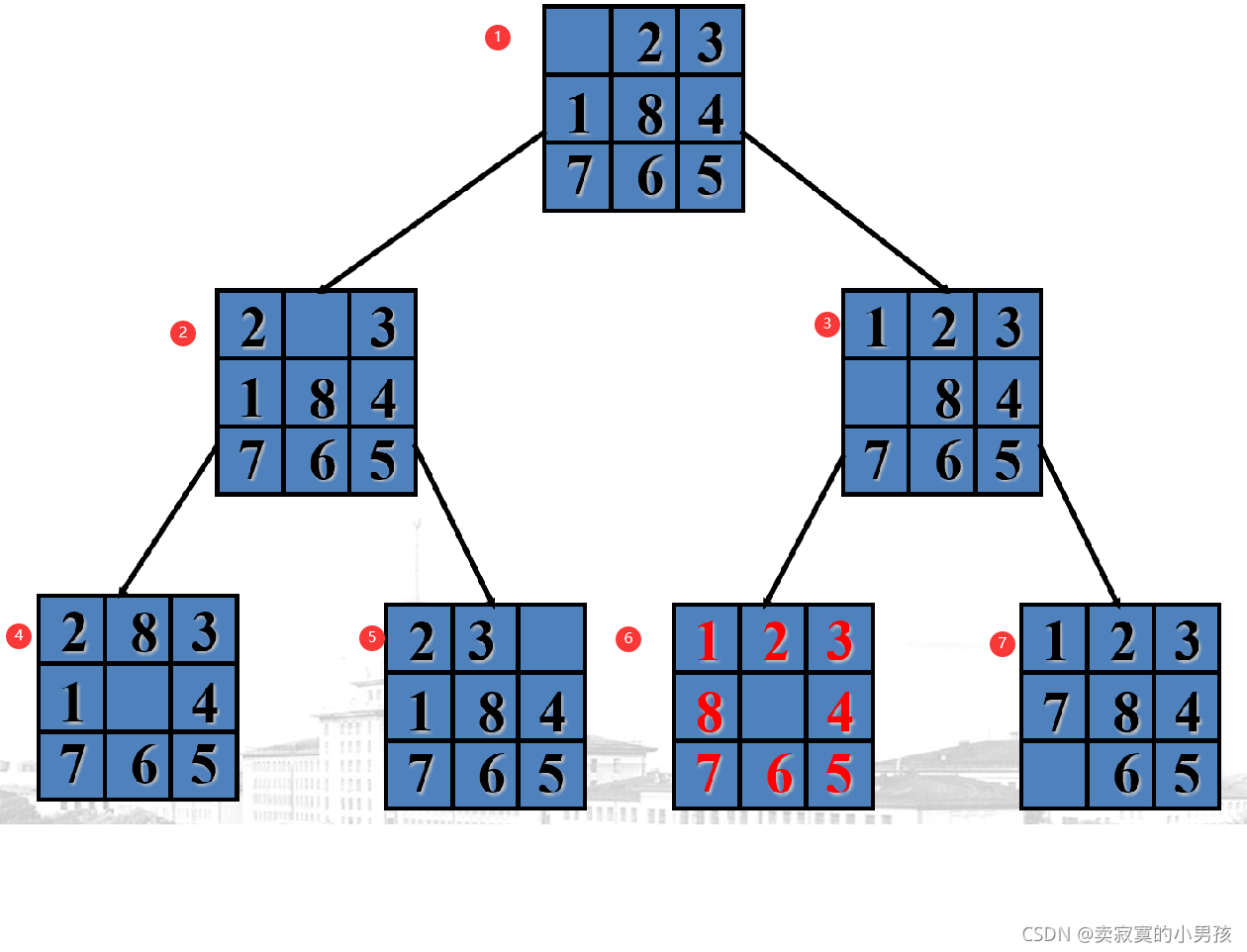
我们可以将移动的方法来作为判断的标准,比如在移动第一个图的时候,我们可以移动1也可以移动2,所以第一个图有两个分支,即2和3两幅图。以此类推。
如果一直画下取有无数张图,我们要在这些图中寻找到排序规整的图,即我们要搜索的图。
利用广度优先遍历来求解。
首先建立一个队列,将根节点放进去:

广度优先遍历最后的遍历顺序是从上向下从左向右一行一行遍历。
深度优先遍历
深度优先搜索的步骤
1.构造一个由根构成的单元素栈S。
2.如果栈顶元素是目标节点则停止遍历。
3.出栈,并将出栈元素的子节点全部压入栈顶。
4.如果栈空则失败。
求解puzzle问题
根据上面那幅图,首先将根节点入栈。
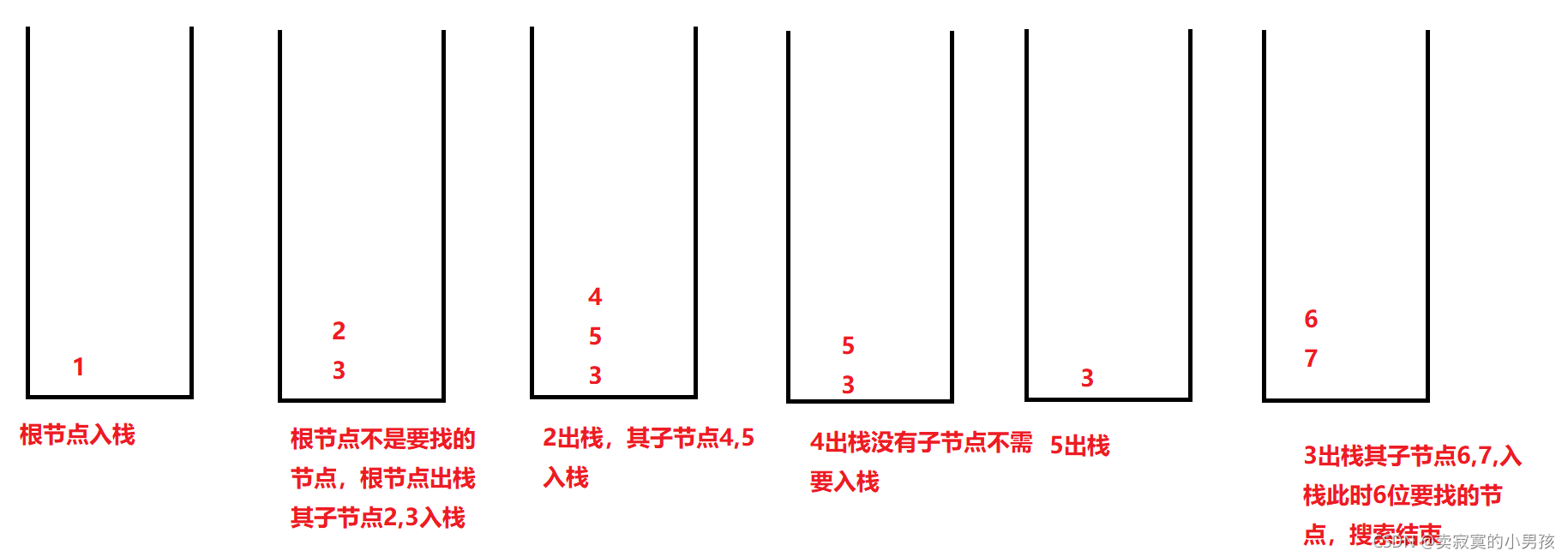
我们发现深度优先遍历和广度优先遍历的算法结构大致相同,都是根节点出,其子节点入,只不过广度优先使用的是队列,深度优先使用的是队列。
搜索的优化
爬山法
爬山法是深度优先搜索的优化,通过引入测度函数来选择优先进行深度优先遍历的节点。
1.构建根节点组成的栈S
2.如果栈顶元素是目标节点则停止遍历。
3.出栈,将出栈节点按测度大小进行入栈,并循环下去。
4.如果栈空则失败。
求解puzzle问题
首先建立一个测度函数,这个函数的建立最好涉及到所有的变量,比如可以定义为f(n)表示的是节点中处于错误位置的节点。
比如对于这个图,共有三个数字放错了位置,分别是1,2,8所以其测度函数f(n)的值为3,我们希望测度函数的值越小越好,所以要优先遍历测度函数小的节点。
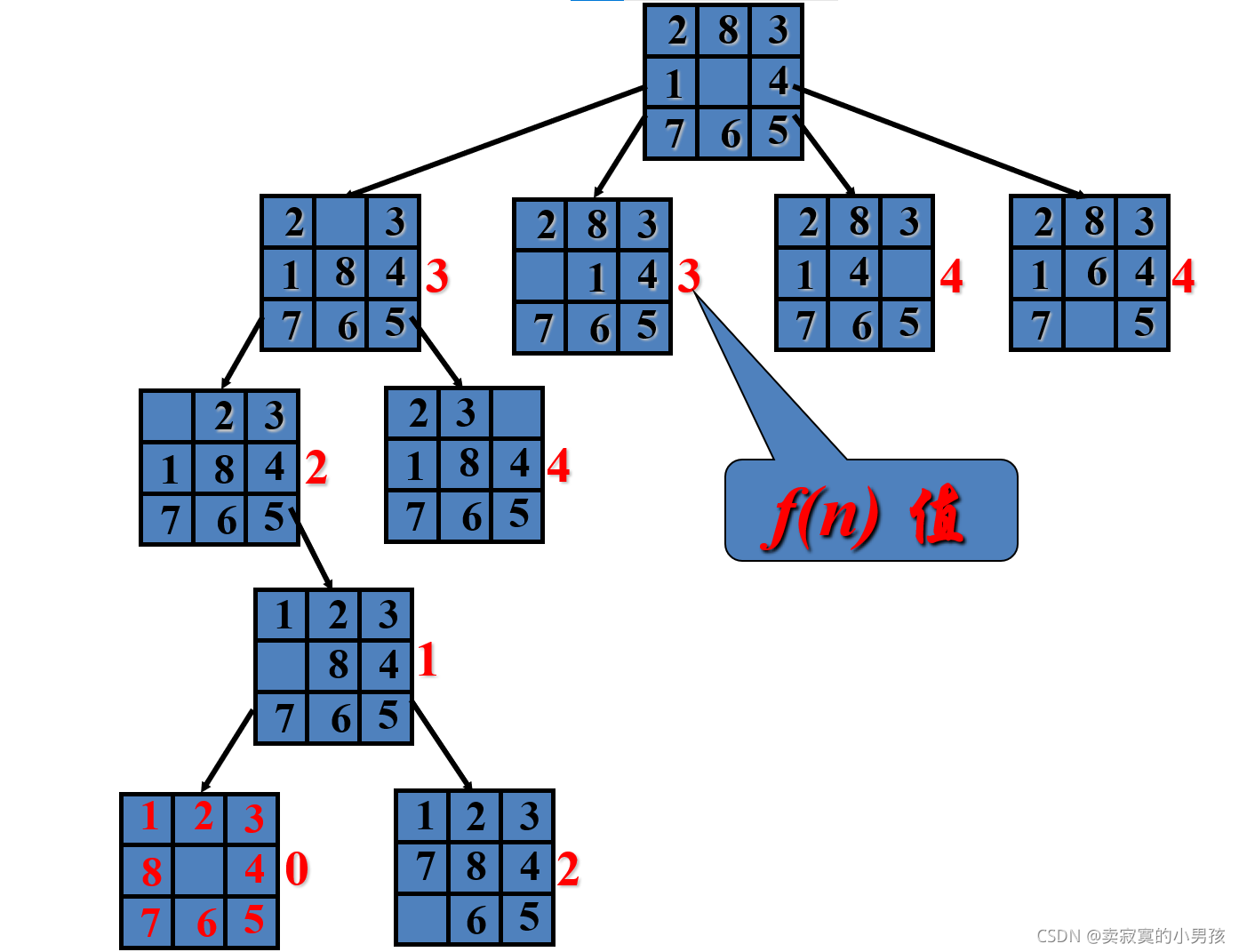
对于深度优先遍历来说,当找出某节点的子节点之后,计算这些子节点的测度值,先选择最小的进行遍历。通过改变其入栈的顺序来实现。
注意:这里并不满足贪心算法求全局最优解,只是设定了一个比较容易找到目标节点的方向
Best-First搜索策略
Best-First算法弥补了爬山法在贪心算法使用上的不足,爬山法只是根据局部的最优解,而Best-First算法则利用到了全局最优解。
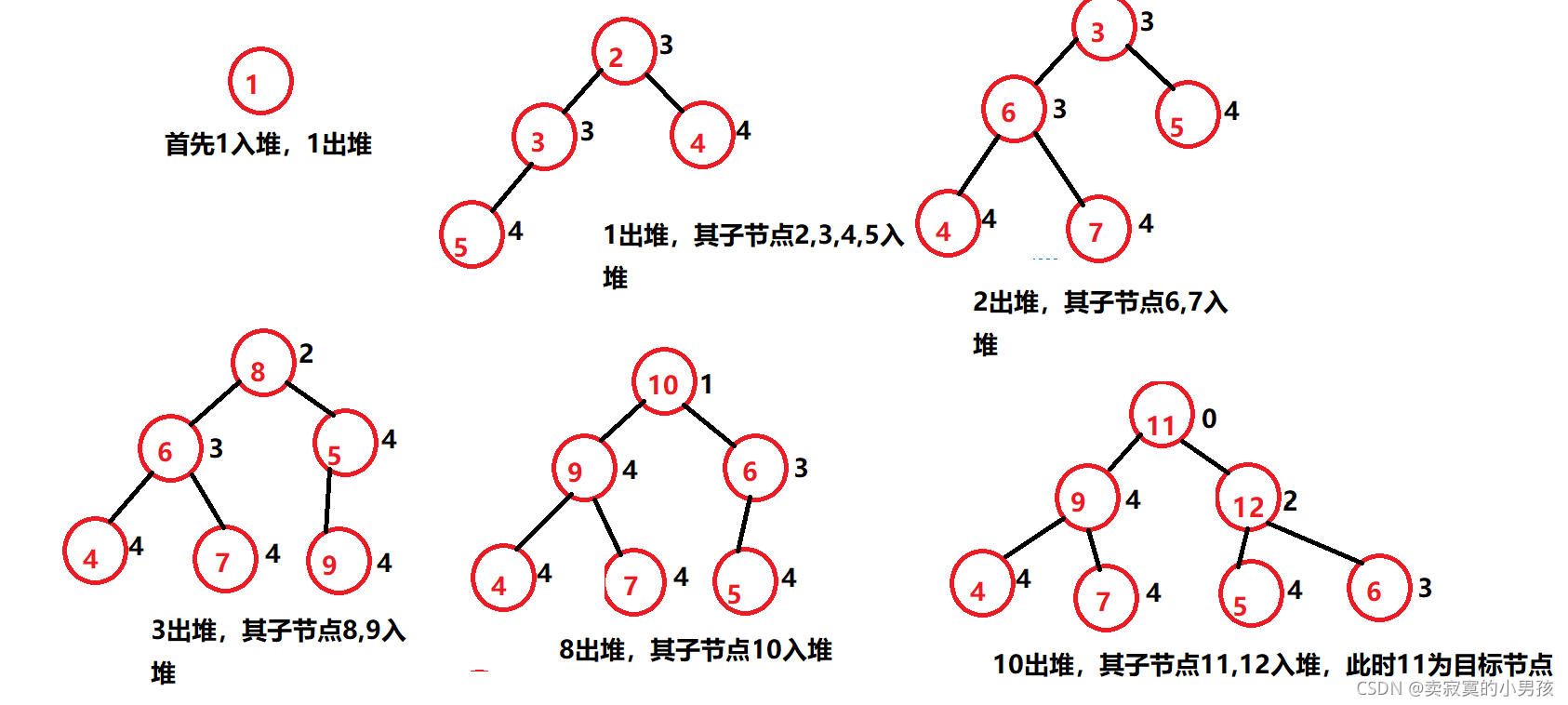
1.使用测度函数构造一个堆H,首先构造由根组成的单元素堆。
2.从堆中删除堆顶元素,把堆顶元素的子节点插入堆中。
3.如果堆顶元素是目标节点则停止,否则循环下去。
4.如果堆空则查找失败。
求解puzzle问题
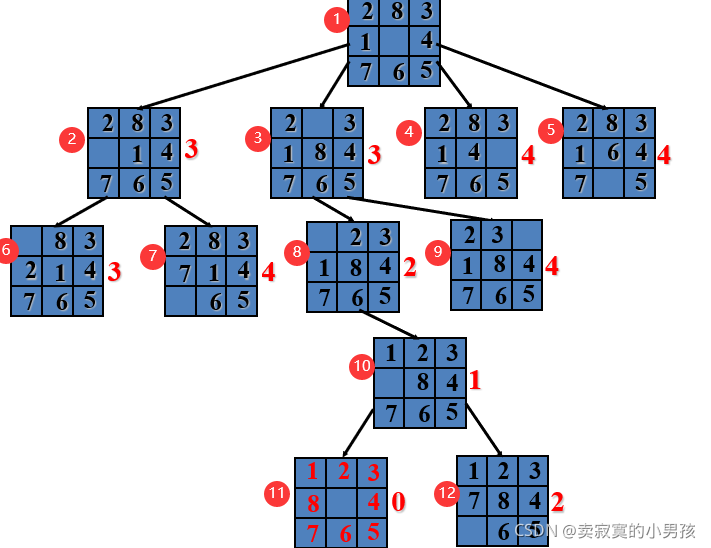
首先我们建立一个堆:
制作不易还望点赞~在线卑微
关于堆的建立,向上调整以及向下调整算法,可以到我的二叉树博客看一看呀,这里就不讲了。
其实堆更像是一个系统而非数据结构,通过其自动的向上向下调整可以时刻找出一组数中的最小值(这里建立的是小堆)。这里就和深度优先还是广度优先就没有关系了,只是单纯地对测度值最小的进行扩展查找。
剪枝法求解最优解问题
剪枝法即减去不可能出现最优解的分支。剪枝法是爬山算法的优化。
求解最短路径问题
输入:一个多阶段图。
输出:从v0到v3的最短路径。
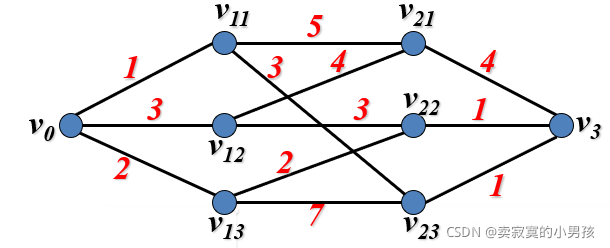
根据图使用爬山法建立树:
首先规定测度值为顶点通过某一条路线到达该节点的距离和。
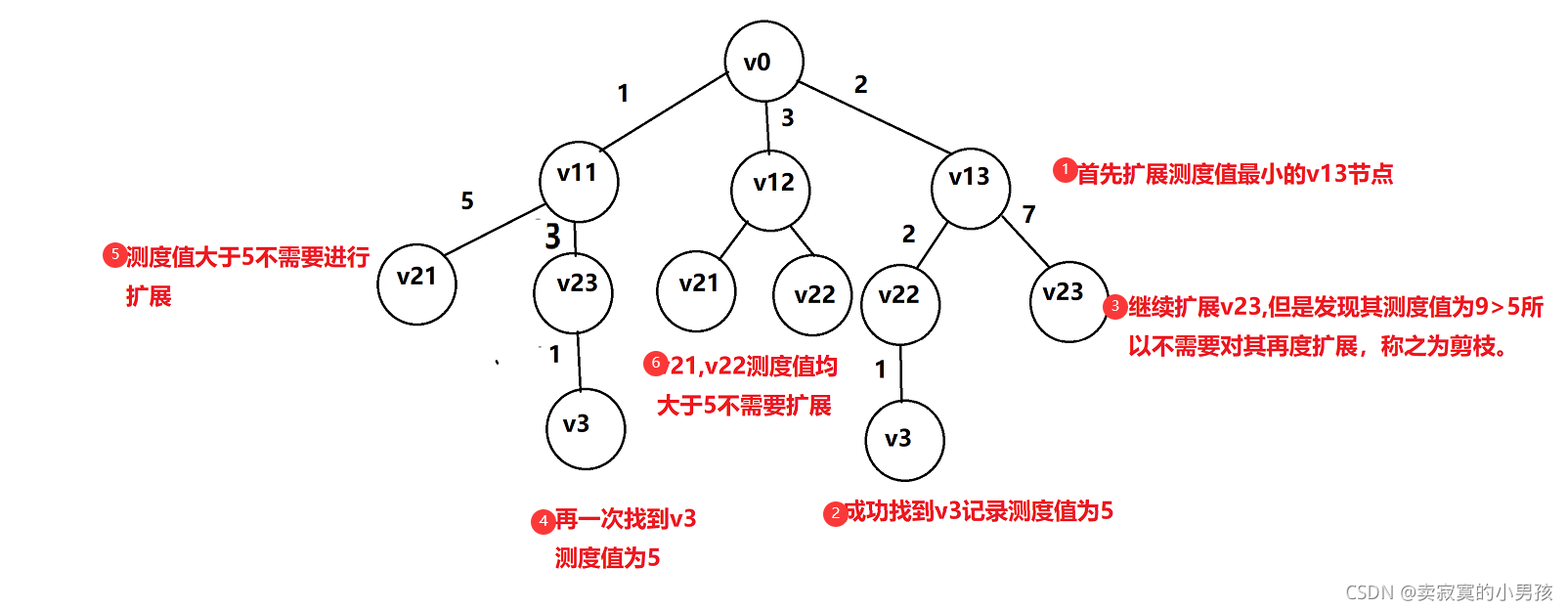
即首先用爬山法局部确定一个大概最小的测度值,然后再扩展其他节点的过程中,如果其测度值大于这个估计的测度值则这条路线一定是不是最小的路线,所以就不需要再去扩展这个节点了,从而实现了剪枝。这里使用排山法而不用Best-First算法的原因是这是一个搜索路径的问题,适合一条路深度优先搜索下去,Best-First更适合查找某一个节点。
搜索算法的应用
人员安排问题
问题定义
输入:
人的集合:P={P1,P2,P3,……Pn}
工作的集合:J={J1,J2,J3……Jn}
矩阵C[i,j]:指的是Pi做Jj工作所需要的代价。
并且J是一个偏序集合,即只有前一个工作结束之后才能进行下一个工作,比如只有在J1结束后才能进行J2
同时对于人也有安排顺序,即当P1安排完才能安排P2。
输出:
如何安排工作使得工作的总代价最低。
求解
基本信息
假设工作的顺序为:
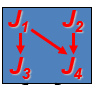
C[i,j]矩阵为:

代价矩阵的化简
在画出搜索树之前,我们可以对代价矩阵进行化简,化简的规则为每一行或者每一列同时减去某一个数,使得每一行每一列都会出现一个0。

得到的12+26+3+10+3=54就是初始代价。
下面解释一下为什么要么算,这么算对结果是否产生影响:
化简代价矩阵的原因是可以方便进行剪枝,这一点下面会说。主要看对结果产生的影响:我们的最后结果实际上是在原来的代价矩阵中每一行,每一列中找到4个值,使之和为最小。假设这四个值是a,b,c,d,我们要的最小代价就为a+b+c+d。由于a,b,c,d分布在不同行上,对不同行进行-12,-26,-3,-10一定会作用到a+b+c+d这个结果上,且每一个减法只作用一次,在纵列上是同理的,-3一定会作用在a+b+c+d这个结果上,并且也只作用一次,因此化简后的矩阵求得的最小代价就是a’+b’+c’+d’=a+b+c+d-12-26-3-10-3=a+b+c+d-54。当未进行选择的时候a’+b’+c’+d’=0,此时代价就可以记为起始代价即为54。然后再在化简后的矩阵中进行选择。
只有当最终结果为代价矩阵中每一行每一列都有取值时才能对其进行化简
建立搜索树
我们根据工作的顺序建立搜索树:
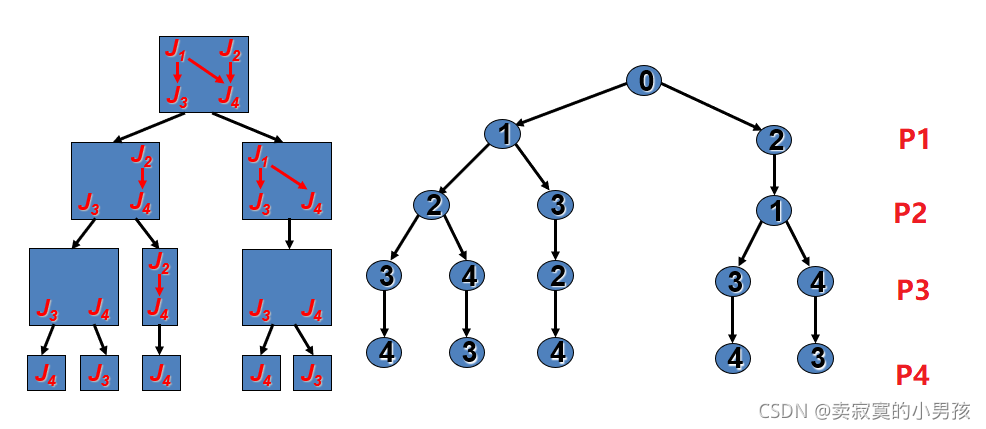
然后确定某节点的测度函数为执行完该节点之前的所有元素的代价和。
剪枝法求解
这里我们也是采用剪枝法,因为要遍历的是路径问题,爬山比Best-First更适合。
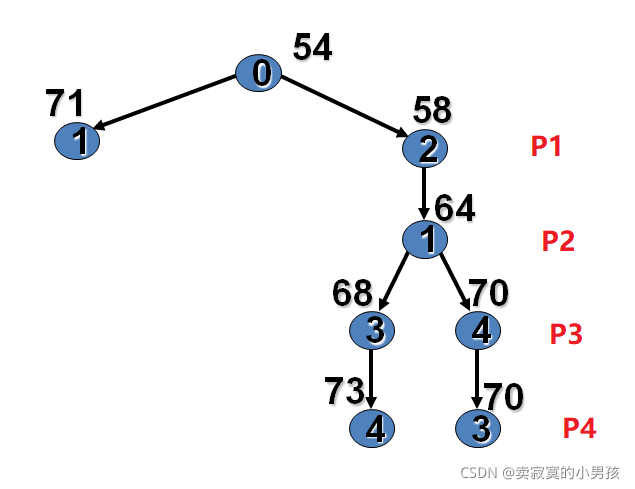
这里就不画图了,口头叙述吧~由于是遍历路径所以我们使用剪枝法,测度函数是总代价
首先建立一个虚拟节点0,它的代价是初始代价54,0入栈出栈之后1,2入栈,经比较发现2的代价较小,对2进行深度优先遍历。得到两个解,这两个解的最终代价分别是73,70。选择最小的70,此时最左侧1的节点的代价是71>70就可以对其进行剪枝,即左侧不需要算了,所以最小的代价是70,分别是P1->J2,P2->J1,P3->J4,P4->J3。
下面来解释一下为什么要化简代价矩阵:
假如不化简,图是建立的搜索树是这样的:
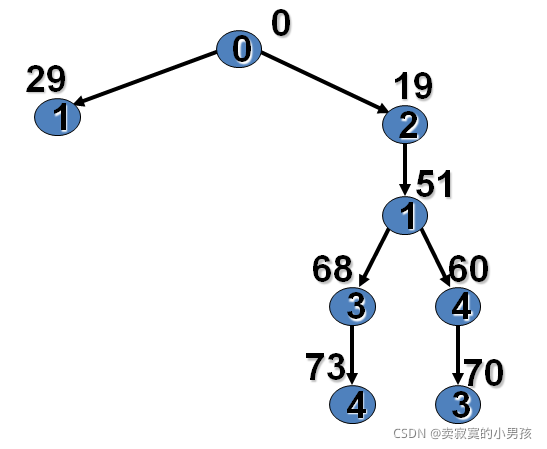
此时发现,70>29并不能进行剪枝,那为什么化简矩阵之后就可以剪枝了呢?首先明确无论是否化简,最终的结果都是一样的,因为无论是否化简矩阵,最后得到的值都是70。化简后的70中包含着必然包含的54,和其他选出来的数;而没有化简的矩阵中只包含了选择的数,这些选择的数中包含了必然包含的54。既然无论如何都会包含这54,那么就可以让它提前显示出来,从而使第一次分支的时候1的节点对应的代价增大,方便进行剪枝。(其实主要是这个54的分配问题,化简的矩阵把它单独提了出来并提前显示了出来,没化简的矩阵54隐含在所选择的节点中)
旅行商问题
问题定义
输入:连通图G=(V,E),每个节点都没有到自身的边,每对节点之间都有一条非负加权边。
输出:一条从任意节点开始,经过每个节点一次,最终返回开始节点的路径
代价矩阵:

求解
对代价矩阵进行化简
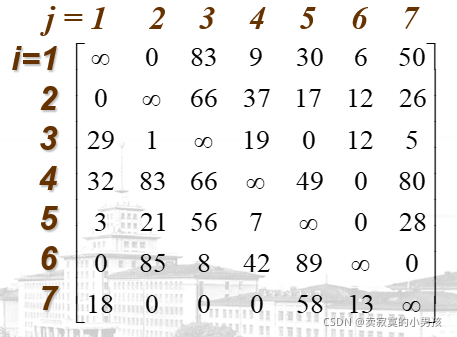
化简之后得到的初始值为96。
建立搜索二叉树
建树的依据
我们根据边来建立搜索二叉树,因为根据节点来建立的话,每一个节点都有一个入边和一个出边,所以它所连接的子节点一定有两个,并不容易处理,因此选择边作为我们的节点。
那么问题又出现了,选择哪条边作为起始的节点呢,选择的依据是什么呢?
1.首先明确我们的目的,我们要尽可能减少计算量来得到最小代价。
2.减小计算量的方法就是进行剪枝。
3.在某一条完整路线的代价与另一条未完成路线的代价比较,当后者大于前者的时候进行剪枝。
我们希望剪枝这个过程尽可能的发生,于是在产生分支的时候,我们希望产生的两个分支的代价尽可能差的多。并以这个差值为依据来选择父节点。
左右子树
在所有的边:(1,2)(2,1)(2,3)(3,2)……中选择分支之后代价差别最大的一条边。假设这条边是(a,b)
那么左节点就是包含这条边的代价,即为96+F(a,b),F(a,b)表示的是(a,b)这条边的代价。右节点就是不包含这条边的代价。
但是我们要进行剪枝,所以我们希望右节点的代价足够的大,可以发现,由于右节点不包含(a,b)所以它一定包含一个从a出发的边和进入b的边,我们不妨取这两种情况的最小值即min(a,x)+min(y,b)+96作为右节点的临时代价,因为右节点的代价一定大于这个值。(注意是临时代价为了分节点用的,并不是要写入的代价)
求解
由于在进行矩阵的化简之后,每一行都有0,所以可以先从0的矩阵节点开始找起,此时的左孩子节点的代价一定小于右孩子的。
在这个矩阵中可以找到(4,6)是使两者差值最大的节点,因此可以从(4,6)划分。注意下图中右子树的L.B不是32+0=128因为这两条最短边不一定被选择,只是一个下界。
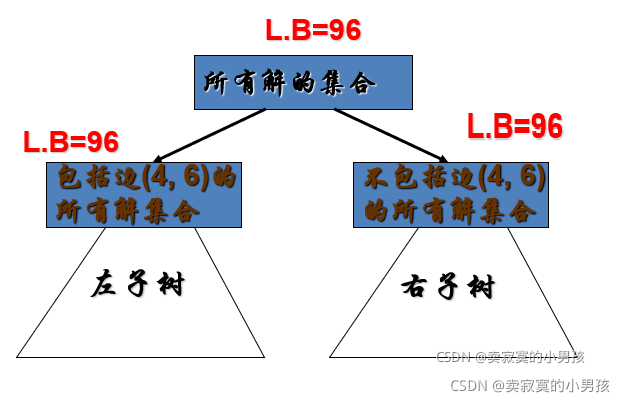
左节点的代价小,因此扩展左节点。在扩展之前可以对矩阵进行进一步的简化:
由于已经选出了(4,6)这条边,那么从4出来的边和从6进入的边都不需要再进行选择了,所以抹去这两行,并且(6,4)也不会被选择了,因此可以将(6,4)置为无穷。
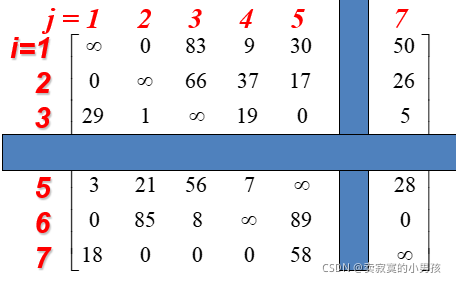
此时对矩阵进行化简,使每一行和每一列都出现0,方便以后的剪枝。剪枝后左节点的代价变成了96+3=99
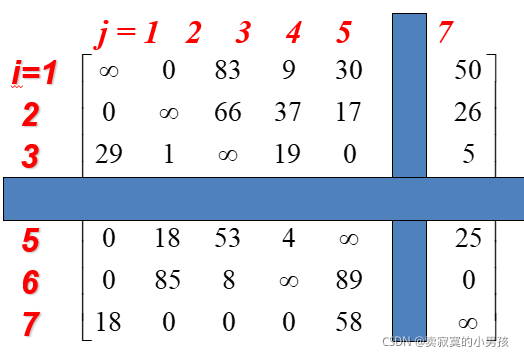
这个矩阵表示的是已经选完(4,6)之后,要在其余的边中选择其他的边的矩阵。
右子树同样也需要变化:由于没选(4,6)所以(4,6)应置为无穷,然后进行矩阵的化简。
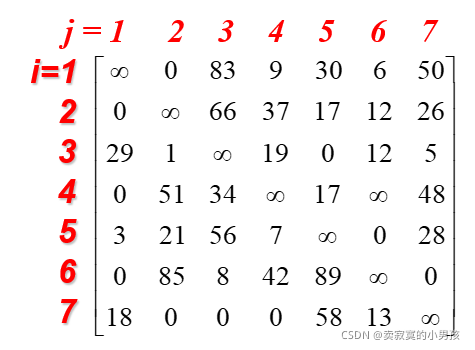
这个矩阵表示的是在不选(4,6)的情况下,在这些边中选择边。右节点的代价为96+32=128
依次类推可以得到这样一棵树:
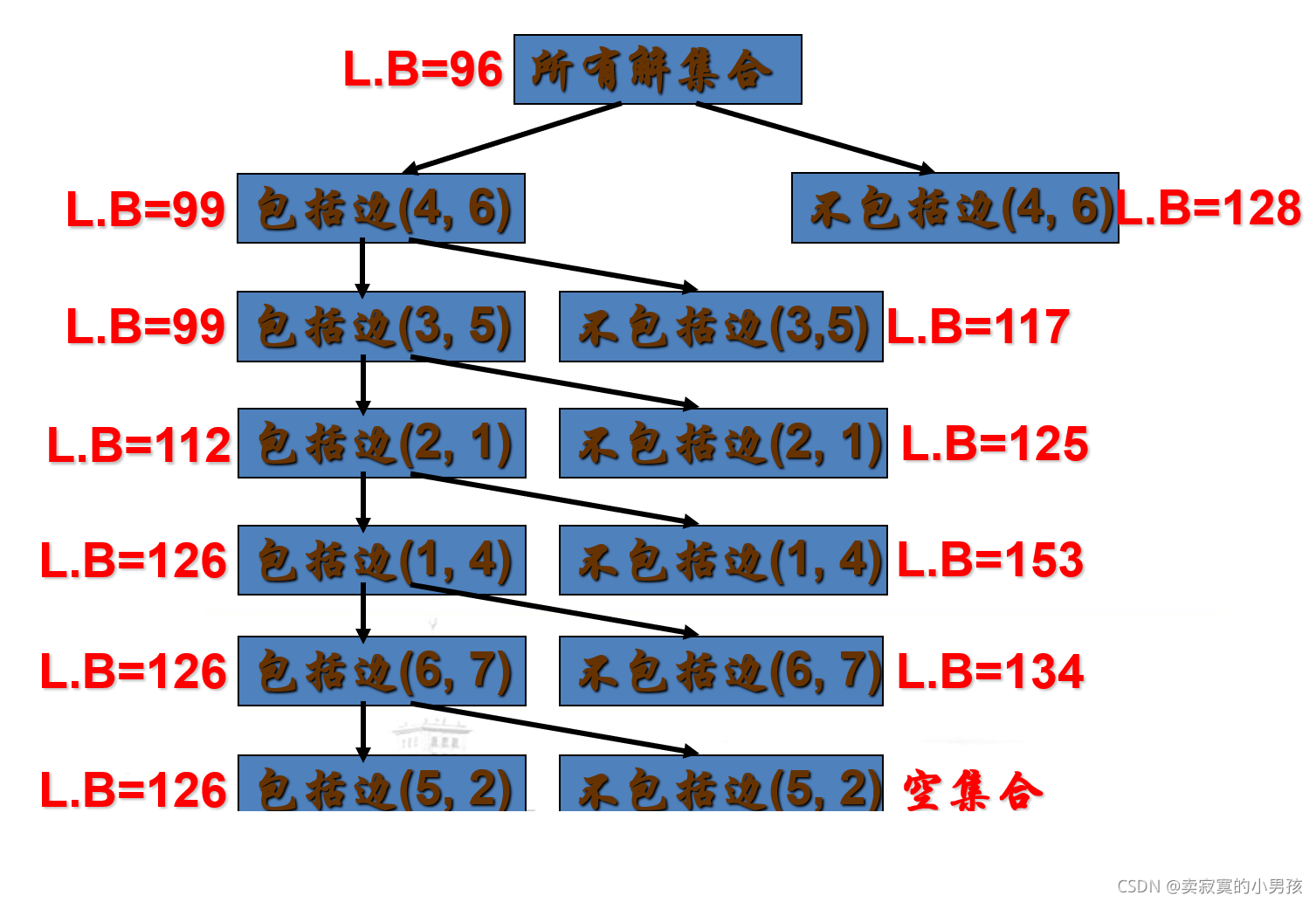
注意右节点的值不是估计值而是矩阵化简之后得到的准确值,区分右节点的临时代价和准确代价
A*算法
什么是A*算法
A*算法其实就是Best-First算法,只不过是在测度函数上考虑了未来的因素。这样做可以更好地连接前后节点,弥补了Best-First算法不适合找路径的问题。
它的测度函数可以表示为F(x)=f(x)+g(x),f(x)表示的是它本身具有的代价,g(x)表示的是未来的最小代价。
举一个例子就清晰了:
寻找最短路径
输入:一张图。
输出:从S到T的最短路径。
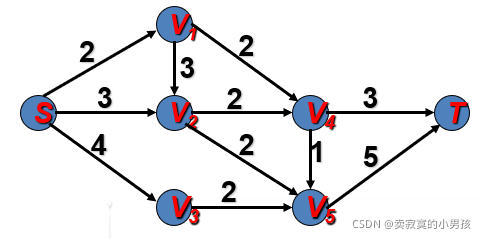
首先根据根节点建立一棵树:令本身具有的代价为g(x),未来的最小代价为h(x),最终节点的代价为f(x)
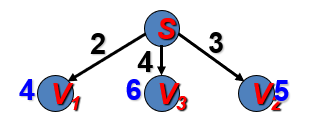
g(v1)=2,h(v1)=min{2,3}=2,f(v1)=2+2=4。
g(v3)=4,h(v3)=min{2}=2, f(v3)=4+2=6。
g(v2)=5,h(v2)=min{2,2}=2,f(v2)=3+2=5。
此时根据Best-First算法扩展潜力最大的节点即代价最小的节点v1
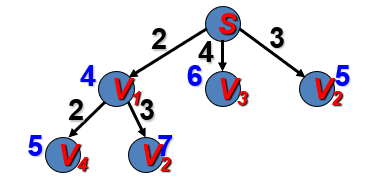
g(v4)=2+2=4 h(v4)=min{1,3}=1 f(v4)=4+1=5
g(v2)=2+3=5 h(v2)=min{2,2}=2 f(v2)=2+5=7
根据Best-First中堆排序的性质,扩展V2(可以自己建堆看一看,就知道为什么不扩展V4了,理论上来说,先扩展的一般都是先出现的)
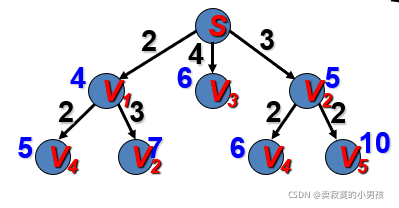
g(v4)=3+2=5 h(v4)=min{3,1}=1 f(v4)=5+1=6
g(v5)=3+2=5 h(v5)=min{5}=5 f(v5)=5+5=10
扩展v4
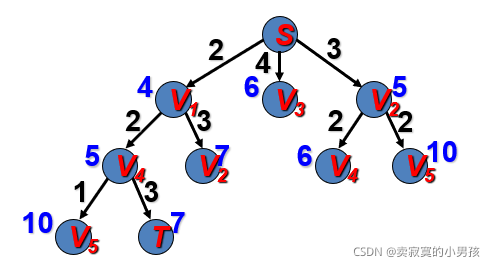
g(v5)=2+2+1=5 h(v5)=min{5}=5 f(v5)=5+5=10
g(T)=3+2+2=7 h(T)=0 f(T)=7
此时得到了一个可能的解为7,可以进行剪枝了,代价大于等于7的可以不进行扩展。
此时扩展V3
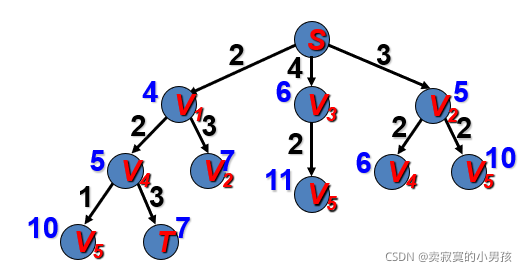
g(v5)=4+2=6 h(v5)=min{5}=5 f(v5)=5+6=11
最后扩展V4
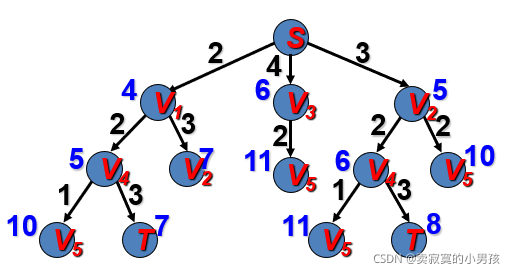
g(v5)=3+2+1=6 h(v5)=min{5}=5 f(v5)=5+6=11
g(T)=3+2+3=8 h(T)=0 f(T)=8+0=8>7
所以最终选择7那条路线,即最短路线为S->v1->v4->T
总结
搜索问题其实只要记住两种类型就可以了一个是Best-First另一个是基于爬山法的剪枝法,其他的都是根据这两个变换出来的,当然最最基础的还是深度优先遍历和堆的实现。好久没更新这个系列了啊,算法类的感觉不肝则已,肝则一天。之前的大部分精力都花费在了二叉树那里,是时候把算法捡起来了,感觉搜索的策略还是比较容易理解的,比之前的数学和动态规划好多了。如果这篇文章对你学习算法中的搜索部分有帮助记得要点个赞啊。