基于python语言,实现经典遗传算法(GA)对多车场(Multi-depot)、异构固定车辆(heterogeneous fixed fleet)、带有服务时间窗(time window)等限制约束的车辆路径规划问题((MD)HVRPTW)进行求解。
1. 适用场景
- 求解HFVRPTW或MDHFVRPTW
- 异构固定车队
- 车辆容量不小于需求节点最大需求
- 车辆路径长度或运行时间无限制
- 需求节点服务成本满足三角不等式
- 节点时间窗至少满足车辆路径只包含一个需求节点的情况
- 多车辆基地或单一
- 各车场车辆总数满足实际需求
2. 求解效果
(1)收敛曲线
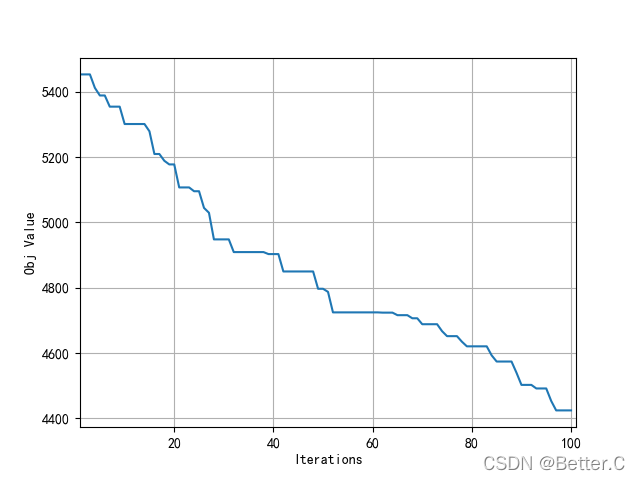
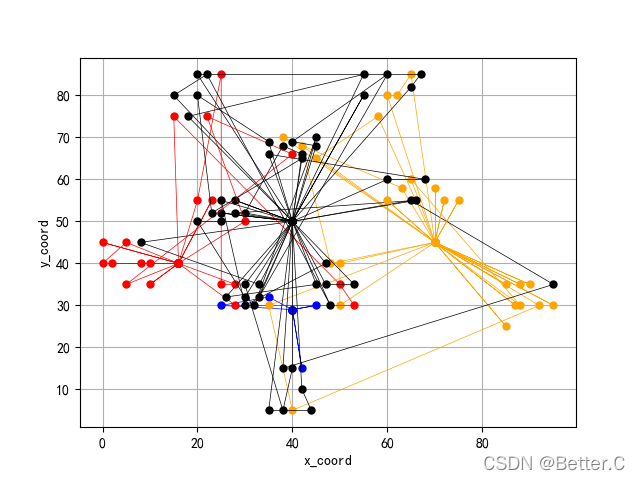
(2)车辆路径
3. 代码分析
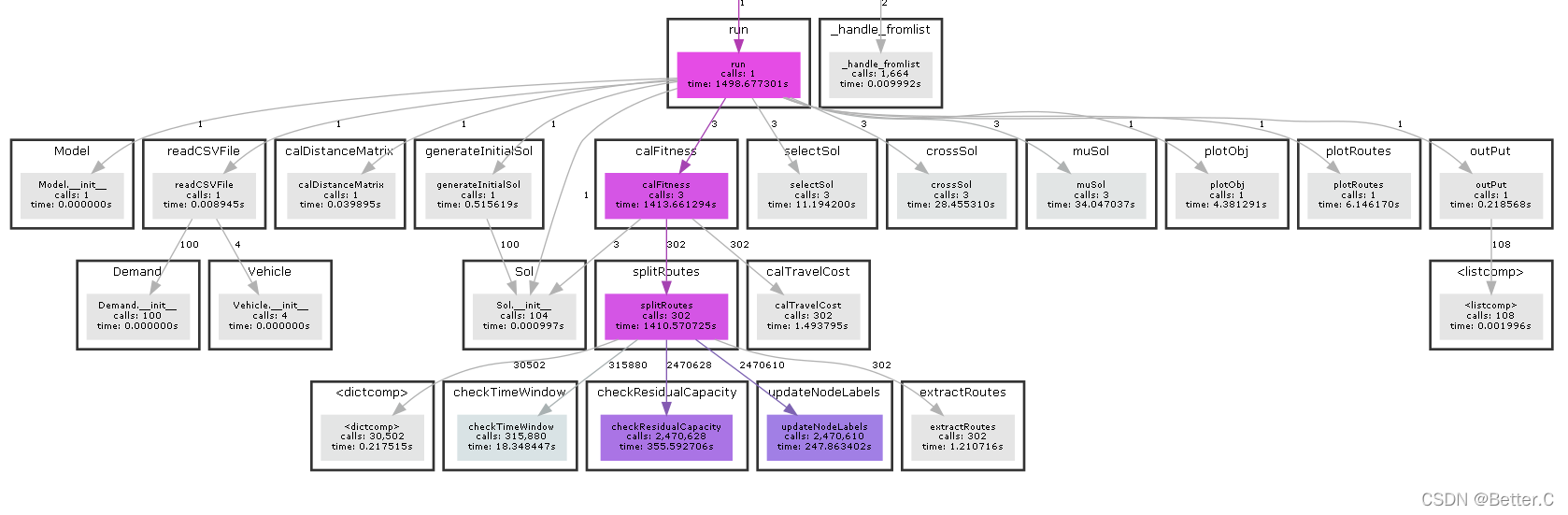
本算法继续采用将所有需求节点构造为一个有序列表的编码方式,并运用在交叉、变异等寻优过程中。当需要评估染色体质量时需采用split方法,在考虑车场、异构固定车队、服务时间窗等约束条件下,将有序列表分割为多个可行的车辆路径。split过程也是整个算法的核心,这里复现文末的参考文献中的算法3,并做了适当微调。整个算法的函数调用关系如下图(采用PyCallGraph绘制)。
4. 数据格式
以csv文件储存数据,其中demand.csv文件记录需求节点数据,共包含需求节点id,需求节点横坐标,需求节点纵坐标,需求量;depot.csv文件记录车场节点数据,共包含车场id,车场横坐标,车场纵坐标,车队类型,车辆容量,车辆速度,车辆数量,车辆固定成本,车辆单位变动成本,车辆最早开始服务时间,车辆最晚结束服务时间。需要注意的是:需求节点id应为整数,从0开始编号,车场节点id任意,但不可与需求节点id重复(建议以 ‘d’+int 形式,便于程序可视化路线)。 可参考github主页相关文件。
5. 分步实现
(1)数据结构
定义Sol()类,Demand()类,Vehicle()类,Model()类,其属性如下表:
- Sol()类,表示一个可行解
| 属性 | 描述 |
|---|---|
| node_id_list | 需求节点id有序排列集合 |
| obj | 优化目标值 |
| fitness | 解的适应度 |
| route_list | 车辆路径集合,对应MDVRPTW的解 |
| timetable_list | 车辆节点访问时间集合,对应MDVRPTW的解 |
| distance_of_routes | 总旅行距离 |
| time_of_routes | 总时间 |
- Demand()类,表示一个需求节点
| 属性 | 描述 |
|---|---|
| id | 物理节点id,需唯一 |
| x_coord | 物理节点x坐标 |
| y_coord | 物理节点y坐标 |
| demand | 物理节点需求 |
| start_time | 最早开始服务(被服务)时间 |
| end_time | 最晚结束服务(被服务)时间 |
| service_time | 需求节点服务时间 |
- Vehicle()类,表示一个车队节点
| 属性 | 描述 |
|---|---|
| depot_id | 车辆归属的车场节点节点id,需唯一 |
| x_coord | 车辆归属车场节点x坐标 |
| y_coord | 车辆归属车场节点y坐标 |
| type | 车辆类型 |
| capacity | 车辆容量 |
| free_speed | 车辆运营速度 |
| fixed_cost | 车辆固定成本 |
| variable_cost | 车辆变动成本 |
| start_time | 最早开始服务时间 |
| end_time | 最晚结束服务时间 |
- Model()类,存储算法参数
| 属性 | 描述 |
|---|---|
| best_sol | 全局最优解,值类型为Sol() |
| demand_dict | 需求节点集合(字典),值类型为Demand() |
| vehicle_dict | 车队集合(字典),值类型为Vehicle() |
| vehicle_type_list | 车队id集合 |
| demand_id_list | 需求节点id集合 |
| sol_list | 种群,值类型为Sol() |
| distance_matrix | 节点距离矩阵 |
| number_of_demands | 需求节点数量 |
| opt_type | 优化目标类型,0:最小旅行距离,1:最小时间成本 |
| pc | 交叉概率 |
| pm | 突变概率 |
| n_select | 优良个体选择数量 |
| popsize | 种群规模 |
(2)文件读取
def readCSVFile(demand_file,depot_file,model):
with open(demand_file,'r') as f:
demand_reader=csv.DictReader(f)
for row in demand_reader:
demand = Demand()
demand.id = int(row['id'])
demand.x_coord = float(row['x_coord'])
demand.y_coord = float(row['y_coord'])
demand.demand = float(row['demand'])
demand.start_time=float(row['start_time'])
demand.end_time=float(row['end_time'])
demand.service_time=float(row['service_time'])
model.demand_dict[demand.id] = demand
model.demand_id_list.append(demand.id)
model.number_of_demands=len(model.demand_id_list)
with open(depot_file, 'r') as f:
depot_reader = csv.DictReader(f)
for row in depot_reader:
vehicle = Vehicle()
vehicle.depot_id = row['depot_id']
vehicle.x_coord = float(row['x_coord'])
vehicle.y_coord = float(row['y_coord'])
vehicle.type = row['vehicle_type']
vehicle.capacity=float(row['vehicle_capacity'])
vehicle.free_speed=float(row['vehicle_speed'])
vehicle.numbers=float(row['number_of_vehicle'])
vehicle.fixed_cost=float(row['fixed_cost'])
vehicle.variable_cost=float(row['variable_cost'])
vehicle.start_time=float(row['start_time'])
vehicle.end_time=float(row['end_time'])
model.vehicle_dict[vehicle.type] = vehicle
model.vehicle_type_list.append(vehicle.type)
(3)计算距离矩阵
def calDistanceMatrix(model):
for i in range(len(model.demand_id_list)):
from_node_id = model.demand_id_list[i]
for j in range(i + 1, len(model.demand_id_list)):
to_node_id = model.demand_id_list[j]
dist = math.sqrt((model.demand_dict[from_node_id].x_coord - model.demand_dict[to_node_id].x_coord) ** 2
+ (model.demand_dict[from_node_id].y_coord - model.demand_dict[to_node_id].y_coord) ** 2)
model.distance_matrix[from_node_id, to_node_id] = dist
model.distance_matrix[to_node_id, from_node_id] = dist
for _, vehicle in model.vehicle_dict.items():
dist = math.sqrt((model.demand_dict[from_node_id].x_coord - vehicle.x_coord) ** 2
+ (model.demand_dict[from_node_id].y_coord - vehicle.y_coord) ** 2)
model.distance_matrix[from_node_id, vehicle.type] = dist
model.distance_matrix[vehicle.type, from_node_id] = dist
(4)分割路径
split过程采用标号法最短路思想,为了避免在搜索过程中产生大量劣质节点标签,通过一定规则删除劣质标签:根据帕累托删除被支配的标签;根据剩余容量与剩余需求决定是否生成新标签。
在搜索过程中需要计算可能车辆路径的成本(时间成本或距离成本),如果采用时间成本,这里为了简化,只计算旅行距离成本,忽略了等待时间成本。但在计算适应度部分是严格按照时间成本内容计算的(旅行时间成本+等待时间成本)。
"检查路径是否满足时间要求,不满足要求则不会产生新的标签"
def checkTimeWindow(route,model,vehicle):
timetable=[]
departure=0
for i in range(len(route)):
if i == 0:
next_node_id = route[i + 1]
travel_time = int(model.distance_matrix[vehicle.type, next_node_id] /vehicle.free_speed)
departure = max(0, model.demand_dict[next_node_id].start_time - travel_time)
timetable.append((int(departure), int(departure)))
elif 1 <= i <= len(route) - 2:
last_node_id = route[i - 1]
current_node_id = route[i]
current_node = model.demand_dict[current_node_id]
travel_time = int(model.distance_matrix[last_node_id, current_node_id] / vehicle.free_speed)
arrival = max(timetable[-1][1] + travel_time, current_node.start_time)
departure = arrival + current_node.service_time
timetable.append((int(arrival), int(departure)))
if departure > current_node.end_time:
departure = float('inf')
break
else:
last_node_id = route[i - 1]
travel_time = int(model.distance_matrix[last_node_id, vehicle.type] / vehicle.free_speed)
departure = timetable[-1][1] + travel_time
timetable.append((int(departure), int(departure)))
if departure<vehicle.end_time:
return True
else:
return False
"当产生新的标签W后,检查剩余的车辆容量之和是否能满足剩余未被检车的检点的总需求,如果总容量<总需求,则舍弃W,表明采用W后会导致解不可行"
"这也是减少无效标签的途径之一"
def checkResidualCapacity(residual_node_id_list,W,model):
residual_fleet_capacity=0
residual_demand = 0
for node_id in residual_node_id_list:
residual_demand+=model.demand_dict[node_id].demand
for k,v_type in enumerate(model.vehicle_type_list):
vehicle=model.vehicle_dict[v_type]
residual_fleet_capacity+=(vehicle.numbers-W[k+4])*vehicle.capacity
if residual_demand<=residual_fleet_capacity:
return True
else:
return False
"由于标号法会产生大量标签,为了降标签数量,减少对劣质标签的搜索,在插入新标签时根据帕累托,删除支配解"
def updateNodeLabels(label_list,W,number_of_lables):
new_label_list=[]
if len(label_list)==0:
number_of_lables += 1
W[0] = number_of_lables
new_label_list.append(W)
else:
for label in label_list:
if W[3]<=label[3] and sum(W[4:])<=sum(label[4:]):
if W not in new_label_list:
number_of_lables += 1
W[0] = number_of_lables
new_label_list.append(W)
elif W[3]<=label[3] and sum(W[4:])>sum(label[4:]):
new_label_list.append(label)
if W not in new_label_list:
number_of_lables += 1
W[0] = number_of_lables
new_label_list.append(W)
elif W[3]>label[3] and sum(W[4:])<sum(label[4:]):
new_label_list.append(label)
if W not in new_label_list:
number_of_lables += 1
W[0] = number_of_lables
new_label_list.append(W)
elif W[3]>label[3] and sum(W[4:])>=sum(label[4:]):
new_label_list.append(label)
return new_label_list,number_of_lables
"根据标号法的求解结果,从中提取出各车辆路径"
def extractRoutes(V,node_id_list,model):
route_list = []
min_obj=float('inf')
pred_label_id=None
v_type=None
# search the min cost label of last node of the node_id_list
for label in V[model.number_of_demands-1]:
if label[3]<=min_obj:
min_obj=label[3]
pred_label_id=label[1]
v_type=label[2]
# generate routes by pred_label_id
route=[node_id_list[-1]]
indexs=list(range(0,model.number_of_demands))[::-1]
start=1
while pred_label_id!=1:
for i in indexs[start:]:
stop=False
for label in V[i]:
if label[0]==pred_label_id:
stop=True
pred_label_id=label[1]
start=i
v_type_=label[2]
break
if not stop:
route.insert(0,node_id_list[i])
else:
route.insert(0,v_type)
route.append(v_type)
route_list.append(route)
route=[node_id_list[i]]
v_type=v_type_
route.insert(0,v_type)
route.append(v_type)
route_list.append(route)
return route_list
"采用标号法对node_id_list进行分割,得到车辆路径"
def splitRoutes(node_id_list,model):
"""
V: dict,key=id,value=[n1,n2,n3,n4,n5,....]
id:node_id_list的索引
n1: 当前标签的生成次序
n2: 生成当前标签的前一个标签的id
n3: 当前标签对应的车辆类型
n4: 当前路径的费用,对应与优化目标,当优化目标为旅行时间时,这里为简化计算只考虑节点间的旅行时间,舍去了等待时间
n5-: 截止到当前标签,各类型车辆的使用数量
这里采用先搜索车辆集合再搜索标签集合的方法,与原文是相反的"
假设有a个标签,n个车需要搜索
若按照原文的搜索顺序:对于任意一个label,都要判断当前路径对于n个车是否满足时间窗要求,搜索次数=a*n;
若按照本文的搜索顺序。对于任意一个车辆类型,若路径不满足时间窗要求则不进行标签搜索,因此搜索次数应<a*n
"""
V={i:[] for i in model.demand_id_list}
V[-1]=[[0]*(len(model.vehicle_type_list)+4)] # -1表示虚拟车场的索引
V[-1][0][0]=1 # 虚拟车场的标签id为1
V[-1][0][1]=1 # 虚拟车场的标签的前向标签也为1
number_of_lables=1
for i in range(model.number_of_demands):
n_1=node_id_list[i]
j=i
load=0
distance={v_type:0 for v_type in model.vehicle_type_list}
while True:
n_2=node_id_list[j]
load=load+model.demand_dict[n_2].demand
stop = False
for k,v_type in enumerate(model.vehicle_type_list):
vehicle=model.vehicle_dict[v_type]
if i == j:
distance[v_type]=model.distance_matrix[v_type,n_1]+model.distance_matrix[n_1,v_type]
else:
n_3=node_id_list[j-1]
distance[v_type]=distance[v_type]-model.distance_matrix[n_3,v_type]+model.distance_matrix[n_3,n_2]\
+model.distance_matrix[n_2,v_type]
route=node_id_list[i:j+1]
route.insert(0,v_type)
route.append(v_type)
if not checkTimeWindow(route,model,vehicle): # 检查时间窗,只有满足时间窗才有可能生成新的标签,否则跳过
continue
for id,label in enumerate(V[i-1]):
if load<=vehicle.capacity and label[k+4]<vehicle.numbers:
stop=True
"计算路径成本,这里计算旅行时间成本时,只考虑节点间的旅行时间,暂不考虑等待时间成本"
if model.opt_type==0:
cost=vehicle.fixed_cost+distance[v_type]*vehicle.variable_cost
else:
cost=vehicle.fixed_cost+distance[v_type]/vehicle.free_speed*vehicle.variable_cost
"由于label是W的前向标签,因此可以在label的基础上生成W"
W=copy.deepcopy(label)
"将W的前向标签id设置为label的id"
W[1]=V[i-1][id][0]
"设置W使用的车辆类型"
W[2]=v_type
"在label的基础上更新W的cost"
W[3]=W[3]+cost
"在label的基础上更新使用的车辆数"
W[k+4]=W[k+4]+1
"检车剩余容量约束,判断是否有可能将W作为当前节点的新的标签"
if checkResidualCapacity(node_id_list[j+1:],W,model):
"根据帕累托将W插入到当前节点的标签列表中,同时删除被支配标签"
label_list,number_of_lables=updateNodeLabels(V[j],W,number_of_lables)
V[j]=label_list
j+=1
if j>=len(node_id_list) or stop==False:
break
if len(V[model.number_of_demands-1])>0:
route_list=extractRoutes(V, node_id_list, model)
return route_list
else:
print("Failed to split the node id list because of the insufficient capacity")
return None
(5)适应度计算
对于解的评价可采用旅行时间成本或旅行距离成本,关于某一条车辆路径的成本计算如下:
- 距离成本=车辆固定成本+旅行距离*变动成本
- 时间成本=车辆固定成本+(旅行时间+等待时间)*变动成本
这里认为单位距离成本=单位旅行时间成本=单位等待时间成本
"计算解的成本,这里对于时间成本包含了节点间旅行时间以及节点处的等待时间"
def calTravelCost(route_list,model):
timetable_list=[]
distance_of_routes=0
time_of_routes=0
obj=0
for route in route_list:
timetable=[]
vehicle=model.vehicle_dict[route[0]]
travel_distance=0
travel_time=0
v_type = route[0]
free_speed=vehicle.free_speed
fixed_cost=vehicle.fixed_cost
variable_cost=vehicle.variable_cost
for i in range(len(route)):
if i == 0:
next_node_id=route[i+1]
travel_time_between_nodes=model.distance_matrix[v_type,next_node_id]/free_speed
departure=max(0,model.demand_dict[next_node_id].start_time-travel_time_between_nodes)
timetable.append((int(departure),int(departure)))
elif 1<= i <= len(route)-2:
last_node_id=route[i-1]
current_node_id=route[i]
current_node = model.demand_dict[current_node_id]
travel_time_between_nodes=model.distance_matrix[last_node_id,current_node_id]/free_speed
arrival=max(timetable[-1][1]+travel_time_between_nodes,current_node.start_time)
departure=arrival+current_node.service_time
timetable.append((int(arrival),int(departure)))
travel_distance += model.distance_matrix[last_node_id, current_node_id]
travel_time += model.distance_matrix[last_node_id, current_node_id]/free_speed+\
+ max(current_node.start_time - arrival, 0)
else:
last_node_id = route[i - 1]
travel_time_between_nodes = model.distance_matrix[last_node_id,v_type]/free_speed
departure = timetable[-1][1]+travel_time_between_nodes
timetable.append((int(departure),int(departure)))
travel_distance += model.distance_matrix[last_node_id,v_type]
travel_time += model.distance_matrix[last_node_id,v_type]/free_speed
distance_of_routes+=travel_distance
time_of_routes+=travel_time
if model.opt_type==0:
obj+=fixed_cost+travel_distance*variable_cost
else:
obj += fixed_cost + travel_time *variable_cost
timetable_list.append(timetable)
return timetable_list,time_of_routes,distance_of_routes,obj
"计算适应度"
def calFitness(model):
max_obj=-float('inf')
best_sol=Sol()
best_sol.obj=float('inf')
number_of_split_failures=0
# calculate travel distance and travel time
for sol in model.sol_list:
node_id_list=copy.deepcopy(sol.node_id_list)
ret=splitRoutes(node_id_list, model)
if ret is not None:
sol.route_list=ret
sol.timetable_list, sol.time_of_routes, sol.distance_of_routes, sol.obj=calTravelCost(sol.route_list,model)
if sol.obj > max_obj:
max_obj=sol.obj
if sol.obj < best_sol.obj:
best_sol=copy.deepcopy(sol)
else:
number_of_split_failures+=1
sol.obj=None
# calculate fitness
for sol in model.sol_list:
sol.fitness=max_obj-sol.obj if sol.obj is not None else max_obj
if best_sol.obj<model.best_sol.obj:
model.best_sol=copy.deepcopy(best_sol)
if number_of_split_failures>=model.popsize*0.3:
print("There are {} sols that are unfeasible. Please increase the number of vehicles to obtain better solutions."
.format(number_of_split_failures))
(6)初始解生成
def generateInitialSol(model):
demand_id_list=copy.deepcopy(model.demand_id_list)
for i in range(model.popsize):
seed=int(random.randint(0,10))
random.seed(seed)
random.shuffle(demand_id_list)
sol=Sol()
sol.node_id_list=copy.deepcopy(demand_id_list)
model.sol_list.append(sol)
(7)优良个体选择
def selectSol(model):
sol_list=copy.deepcopy(model.sol_list)
model.sol_list=[]
for i in range(model.n_select):
f1_index=random.randint(0,len(sol_list)-1)
f2_index=random.randint(0,len(sol_list)-1)
f1_fit=sol_list[f1_index].fitness
f2_fit=sol_list[f2_index].fitness
if f1_fit<f2_fit:
model.sol_list.append(sol_list[f2_index])
else:
model.sol_list.append(sol_list[f1_index])
(8)交叉
def crossSol(model):
sol_list=copy.deepcopy(model.sol_list)
model.sol_list=[]
while True:
f1_index = random.randint(0, len(sol_list) - 1)
f2_index = random.randint(0, len(sol_list) - 1)
if f1_index!=f2_index:
f1 = copy.deepcopy(sol_list[f1_index])
f2 = copy.deepcopy(sol_list[f2_index])
if random.random() <= model.pc:
cro1_index=int(random.randint(0,len(model.demand_id_list)-1))
cro2_index=int(random.randint(cro1_index,len(model.demand_id_list)-1))
new_c1_f = []
new_c1_m=f1.node_id_list[cro1_index:cro2_index+1]
new_c1_b = []
new_c2_f = []
new_c2_m=f2.node_id_list[cro1_index:cro2_index+1]
new_c2_b = []
for index in range(len(model.demand_id_list)):
if len(new_c1_f)<cro1_index:
if f2.node_id_list[index] not in new_c1_m:
new_c1_f.append(f2.node_id_list[index])
else:
if f2.node_id_list[index] not in new_c1_m:
new_c1_b.append(f2.node_id_list[index])
for index in range(len(model.demand_id_list)):
if len(new_c2_f)<cro1_index:
if f1.node_id_list[index] not in new_c2_m:
new_c2_f.append(f1.node_id_list[index])
else:
if f1.node_id_list[index] not in new_c2_m:
new_c2_b.append(f1.node_id_list[index])
new_c1=copy.deepcopy(new_c1_f)
new_c1.extend(new_c1_m)
new_c1.extend(new_c1_b)
f1.nodes_seq=new_c1
new_c2=copy.deepcopy(new_c2_f)
new_c2.extend(new_c2_m)
new_c2.extend(new_c2_b)
f2.nodes_seq=new_c2
model.sol_list.append(copy.deepcopy(f1))
model.sol_list.append(copy.deepcopy(f2))
else:
model.sol_list.append(copy.deepcopy(f1))
model.sol_list.append(copy.deepcopy(f2))
if len(model.sol_list)>model.popsize:
break
(9)突变
def muSol(model):
sol_list=copy.deepcopy(model.sol_list)
model.sol_list=[]
while True:
f1_index = int(random.randint(0, len(sol_list) - 1))
f1 = copy.deepcopy(sol_list[f1_index])
m1_index=random.randint(0,len(model.demand_id_list)-1)
m2_index=random.randint(0,len(model.demand_id_list)-1)
if m1_index!=m2_index:
if random.random() <= model.pm:
node1=f1.node_id_list[m1_index]
f1.node_id_list[m1_index]=f1.node_id_list[m2_index]
f1.node_id_list[m2_index]=node1
model.sol_list.append(copy.deepcopy(f1))
else:
model.sol_list.append(copy.deepcopy(f1))
if len(model.sol_list)>model.popsize:
break
(10)绘制收敛曲线
def plotObj(obj_list):
plt.rcParams['font.sans-serif'] = ['SimHei'] #show chinese
plt.rcParams['axes.unicode_minus'] = False # Show minus sign
plt.plot(np.arange(1,len(obj_list)+1),obj_list)
plt.xlabel('Iterations')
plt.ylabel('Obj Value')
plt.grid()
plt.xlim(1,len(obj_list)+1)
plt.show()
(11)绘制车辆路线
def plotRoutes(model):
for route in model.best_sol.route_list:
x_coord=[model.vehicle_dict[route[0]].x_coord]
y_coord=[model.vehicle_dict[route[0]].y_coord]
for node_id in route[1:-1]:
x_coord.append(model.demand_dict[node_id].x_coord)
y_coord.append(model.demand_dict[node_id].y_coord)
x_coord.append(model.vehicle_dict[route[-1]].x_coord)
y_coord.append(model.vehicle_dict[route[-1]].y_coord)
plt.grid()
if route[0]=='v1':
plt.plot(x_coord,y_coord,marker='o',color='black',linewidth=0.5,markersize=5)
elif route[0]=='v2':
plt.plot(x_coord,y_coord,marker='o',color='orange',linewidth=0.5,markersize=5)
elif route[0]=='v3':
plt.plot(x_coord,y_coord,marker='o',color='r',linewidth=0.5,markersize=5)
else:
plt.plot(x_coord, y_coord, marker='o', color='b', linewidth=0.5, markersize=5)
plt.xlabel('x_coord')
plt.ylabel('y_coord')
plt.show()
(12)输出结果
def outPut(model):
work=xlsxwriter.Workbook('result.xlsx')
worksheet=work.add_worksheet()
worksheet.write(0, 0, 'time_of_routes')
worksheet.write(0, 1, 'distance_of_routes')
worksheet.write(0, 2, 'opt_type')
worksheet.write(0, 3, 'obj')
worksheet.write(1,0,model.best_sol.time_of_routes)
worksheet.write(1,1,model.best_sol.distance_of_routes)
worksheet.write(1,2,model.opt_type)
worksheet.write(1,3,model.best_sol.obj)
worksheet.write(2, 0,'vehicleID')
worksheet.write(2, 1,'depotID')
worksheet.write(2, 2, 'vehicleType')
worksheet.write(2, 3,'route')
worksheet.write(2, 4,'timetable')
for row,route in enumerate(model.best_sol.route_list):
worksheet.write(row+3,0,str(row+1))
depot_id=model.vehicle_dict[route[0]].depot_id
worksheet.write(row+3,1,depot_id)
worksheet.write(row+3,2,route[0])
r=[str(i)for i in route]
worksheet.write(row+3,3, '-'.join(r))
r=[str(i)for i in model.best_sol.timetable_list[row]]
worksheet.write(row+3,4, '-'.join(r))
work.close()
(13)主函数
def run(demand_file,depot_file,epochs,pc,pm,popsize,n_select,opt_type):
"""
:param demand_file: demand file path
:param depot_file: depot file path
:param epochs: Iterations
:param pc: Crossover probability
:param pm: Mutation probability
:param popsize: Population size
:param n_select: Number of excellent individuals selected
:param opt_type: Optimization type:0:Minimize the cost of travel distance;1:Minimize the cost of travel time
:return:
"""
model=Model()
model.pc=pc
model.pm=pm
model.popsize=popsize
model.n_select=n_select
model.opt_type=opt_type
readCSVFile(demand_file,depot_file,model)
calDistanceMatrix(model)
generateInitialSol(model)
history_best_obj = []
best_sol=Sol()
best_sol.obj=float('inf')
model.best_sol=best_sol
start_time=time.time()
for ep in range(epochs):
calFitness(model)
selectSol(model)
crossSol(model)
muSol(model)
history_best_obj.append(model.best_sol.obj)
print("%s/%s, best obj: %s, runtime: %s" % (ep+1,epochs,model.best_sol.obj,time.time()-start_time))
plotObj(history_best_obj)
plotRoutes(model)
outPut(model)
6. 完整代码
如有错误,欢迎交流。
代码和数据文件可从github主页免费获取:
https://github.com/PariseC/Algorithms_for_solving_VRP
参考
- Order-first split-second methods for vehicle routing problems: A review