[数据结构与算法]十大排序之归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

• 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法)
• 自下而上的迭代

1.算法步骤

1.1.递归法

1. 一直递推下去，直到分解的每一个段（seg）中包含一个数组元素（最基本的段），如下图前半部分所示

2. 将每个段进行归并，归并的过程中段的大小呈2倍增长，如上图后半部分所示。

1.2.迭代法

相比较递归而言，迭代已经省略了递推的步骤，而直接进行回溯。

回溯的起点是段（seg）中包含一个数组元素

2.动图演示

3.代码实现

3.1.递归实现

3.1.1.算法实现

void merge_recursive_sort(int arr[], int reg[], int start, int end)
{
	if (start>=end)//递归终止条件
	{
		return;
	}
	int len = end - start; int mid = (len >> 1) + start;
	int start1 = start; int end1 = mid;
	int start2 = mid + 1; int end2 = end;
	merge_recursive_sort(arr, reg, start1, end1);//左递归：更改下顺序
	merge_recursive_sort(arr, reg, start2, end2);//右递归
	int k = start;
	while (start1 <= end1 && start2 <= end2) reg[k++] = arr[start1]<arr[start2] ? arr[start1++] : arr[start2++];
	while (start1 <= end1) reg[k++] = arr[start1++];
	while (start2 <= end2) reg[k++] = arr[start2++];
	for (k=start; k<=end;k++)//将start改为0试试
		arr[k] = reg[k];
}
void merge_sort_recursion(int arr[], int len)//默认是对int类型的数组进行数据交换
{
	int* reg = malloc(sizeof(*arr) * len);//开辟一个和数组大小一样的内存块
	merge_recursive_sort(arr, reg, 0, len - 1);//递归排序
}

3.1.2.测试程序

	int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70,32};//定义一个待排序的数组
	int len = sizeof(arr) / sizeof(*arr);//获取数组长度
	printf("\nsort before\n");
	for (int i = 0; i < len; i++)//打印排序前数组元素
	{
		printf("%d\t", arr[i]);
	}
	merge_sort_recursion(arr,len);//进行归并排序
	printf("\merge_sort_recursion after\n");//打印归并排序后数组元素
	for (int i = 0; i < len; i++)
	{
		printf("%d\t", arr[i]);
	}

3.1.3.疑问

把merge_recursive_sort函数中的代码块

	for (k=start; k<=end;k++)//从start所指示的元素到end所指示的元素进行拷贝
		arr[k] = reg[k];

改为：

	for (k=0; k<=end;k++)//从第0个元素到end所指示的元素进行拷贝
		arr[k] = reg[k];

观看一下结果，你会发现最后排序的结果是一样的。想一下这是为什么。

3.1.4.现象

大家再仔细看看动态显示。你会发现当我们在对后面一段元素进行操作的时候，前面一段元素已经排好序了。

而由于递归的过程中，进行下一次选择之前，是将reg中的内容拷贝至arr

换句话说：

arr数组元素和reg数组元素内容完全一致

3.1.5.解释

之所以会出现将k=start 改为 k=0实验现象一致，或者说arr数组元素和reg数组元素内容完全一致，那是因为我们实现的是先左递归，然后右递归，如果更改次序，就会出现不同的结果。

3.1.6.验证

我们将merge_sort_recursion函数增加一些语句，以显示arr和reg这两个数组。

void merge_sort_recursion(int arr[], int len)//默认是对int类型的数组进行数据交换
{
	int* reg = malloc(sizeof(*arr) * len);
	merge_recursive_sort(arr, reg, 0, len - 1);
	printf("arr array\n");
	for (int i = 0; i < len; i++)//显示arr数组
	{
		printf("%d\t",arr[i]);
	}
	printf("reg array\n");
	for (int i = 0; i < len; i++)//显示reg数组
	{
		printf("%d\t", reg[i]);
	}
}

3.1.6.1.左递归先开始

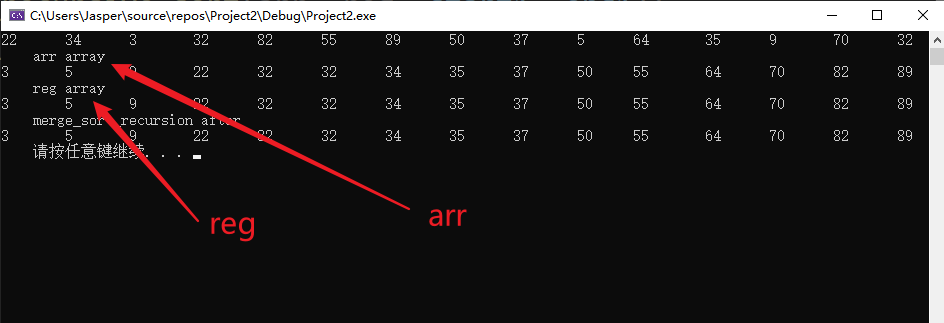
我们发现arr 和 reg 数组元素完全相同。

注意：这个不仅是最终结果的相同，而且是在递归的过程中慢慢的相同（前面的先递归，先相同，后面的后递归，后相同）。不然的话，你就无法解释为什么出现将k=start 改为 k=0实验现象一致。

3.1.6.1.右递归先开始

我们发现，上图中arr和reg数组中的元素全部错误。那是因为现在是右边先递归，意思就是后面的递归先相同，前面的递归后相同。

3.1.7.总结

• 归并排序是利用分治法的实现，先递推、后回溯
• 先左再右递归会使得再进行下一次比较之前，reg数组中的已操作的元素与arr数组中的元素一致

3.2.迭代法

3.2.1.算法实现

void merge_sort_iteration(int arr[], int len)
{
	int* a = arr;
	int* b = malloc(sizeof(*arr) * len);
	for (int seg = 1; seg < len; seg+=seg)//段的增加乘2倍增长，但不可能超过
	{										//len
		for (int start = 0; start < len; start+=seg+seg)//每次加2倍
		{												//seg长度
			int low = start, mid = myMin(start + seg, len),high = myMin(start+seg+seg,len);
			int start1 = low; int end1 = mid;
			int start2 = mid; int end2 = high;
			int k = start;
			while (start1<end1&&start2<end2)//mid为段中高维的部分的第一个
                							//元素，因此是小于，不是小于等于
			b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
			while (start1 < end1)b[k++] = a[start1++];
			while (start2 < end2)b[k++] = a[start2++];

		}
		int* temp = a;//这里参考下面的图，每更新一次数组，就交换指针，这样
		a = b;			//原有数组中的元素就“过期了”（垃圾数据）
		b = temp;
	}
	if (a!=arr)//如果a此时指向的不是arr，就交换一下即可
	{
		int i;
		for (i = 0; i < len; i++)
		{
			b[i] = a[i];
		}
		b = a;
	}
	free(b);
}

3.2.2.测试程序

	int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70,32};//定义一个待排序的数组
	int len = sizeof(arr) / sizeof(*arr);
	printf("\nsort before\n");
	for (int i = 0; i < len; i++)
	{
		printf("%d\t", arr[i]);
	}
	merge_sort_iteration(arr, len);//归并排序
	printf("\merge_sort_iteration after\n");
	for (int i = 0; i < len; i++)
	{
		printf("%d\t", arr[i]);
	}

3.2.3.理解

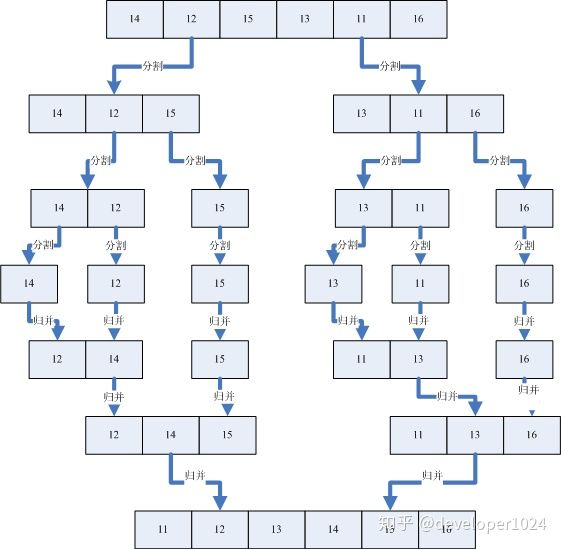
看该图的后半部分。

4.总结

归并排序有两种方法实现：

• 迭代法：以seg=1开始进行迭代
• 递归法：采用分治法的思想，先递推，然后回溯。