文章目录
1.🚀栈
1.1 栈源代码
🌟🌟🌟→可动态增长的栈←🌟🌟🌟
1.2 栈的概念
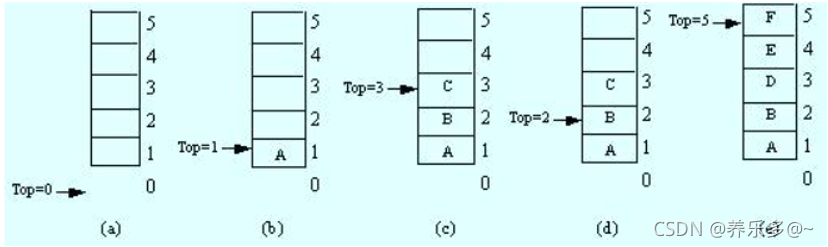
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端
称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
1.2 栈的实现
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的
代价比较小。
栈就像是一个箱子,当你往里放东西时,后放的会压在之前放的上面,而当你想要拿出来时,只能从顶部一个一个的拿取。
而数组也可以实现静态数组和动态增长数组,在这里我们使用动态数组实现可以动态增长的栈
1.2.1 栈的结构
静态栈的结构:
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
动态增长栈的结构:
typedef int STDataType;
typedef struct Stack
{
STDataType* a;//用指针来指向动态开辟的空间
int top; // 栈顶
int capacity; // 容量
}Stack;
1.2.2 栈的初始化
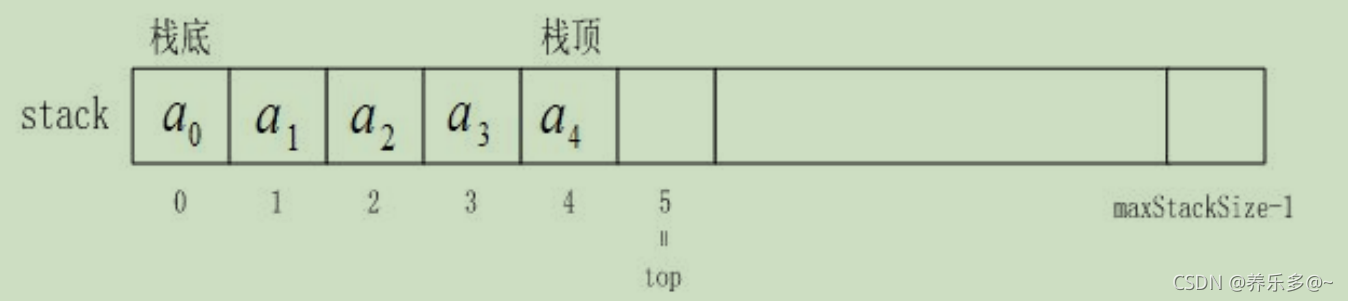
定义ps->top的初始大小为0,也就是说ps->top总是指向栈顶元素的上方
//栈的初始化
void StackInit(Stack* ps){
assert(ps);
int N = 5;
ps->a = (STDataType*)malloc(sizeof(STDataType)*N);//动态开辟,初始大小为5
ps->capacity = N;
ps->top = 0;
}
扩容的方法:
如果栈顶top的大小等于栈的容量capacity则我们定义一个新的大小newcapacity让它等于原来容量的二倍
再将原来栈中的元素放到新栈之中,让指针指向新开辟的栈,完成栈的扩容。
//检测栈是否满,如果满则扩容到原来的二倍
void CheckCapacity(Stack* ps){
if (ps->capacity == ps->top){
int newcapacity = ps->capacity * 2;
STDataType* newps = (STDataType*)malloc(sizeof(STDataType)*newcapacity);
for (int i = 0; i < ps->top; ++i){
newps[i] = ps->a[i];
}
free(ps->a);
ps->a = newps;
ps->capacity = newcapacity;
}
}
1.2.3 入栈
入栈之前需要检测是否需要扩容,入栈需要从栈顶入,即将新元素放到数组top的位置。
// 入栈
void StackPush(Stack* ps, STDataType data){
assert(ps);
CheckCapacity(ps);
ps->a[ps->top] = data;
ps->top++;
}
1.2.4 出栈
注意:出栈表示移除栈顶元素,并非输出栈顶元素
出栈之前我们需要判断栈是否为空(如果为空不能进行出栈操作)。用函数封装起来
如果top的大小为0即表示该栈为空
//判空
int StackEmpty(Stack* ps){
return 0 == ps->top;
}
// 出栈
void StackPop(Stack* ps){
assert(ps);
if (StackEmpty(ps)){
return;
}
ps->top--;
}
1.2.5 获取栈顶元素
这里才是输出栈顶的元素,不过要想连续输出,需要配合出栈交替使用
刚才介绍过top表示栈顶的下一个位置,所以栈顶的元素位置在top-1 的位置
也需要判断栈是否为空,用了assert函数,如果为空将中止程序,也可改为If语句
STDataType StackTop(Stack* ps){
assert(!StackEmpty(ps));
return ps->a[ps->top - 1];
}
1.2.6 获取栈中有效元素个数
有效个数即存储的元素个数,即为top的大小,输出即可,但是要注意需要有接收,可以用printf直接输出或者赋值给其他变量
// 获取栈中有效元素个数
int StackSize(Stack* ps){
assert(ps);
return ps->top;
}
1.2.7 销毁栈
由于我们是malloc出来的一块空间,为了防止内存泄露,我们需要在程序的最后销毁改栈
void StackDestroy(Stack* ps){
assert(ps);
if (ps->a){
free(ps->a);
ps->a = NULL;
ps->capacity = 0;
ps->top = 0;
}
}
2.🚀队列
1.1 队列源代码
🌟🌟🌟→用链表实现队列←🌟🌟🌟
1.2 队列的概念
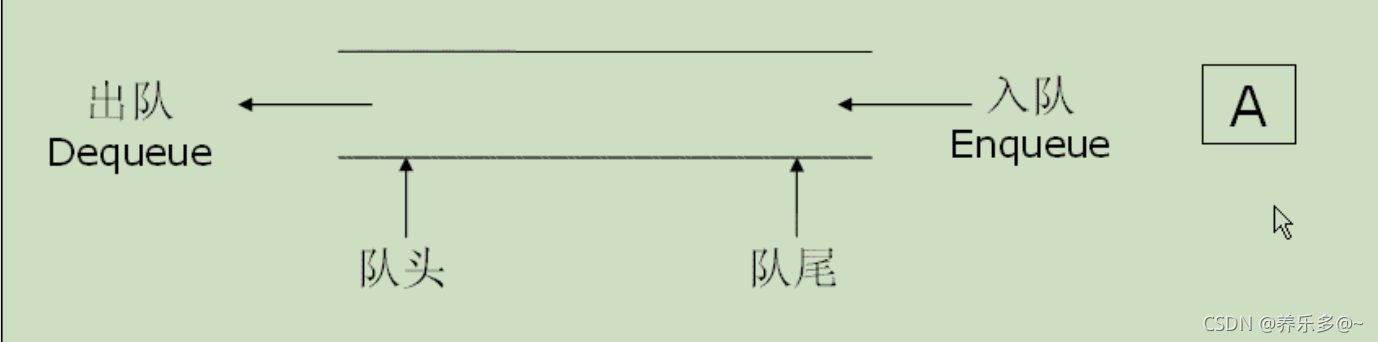
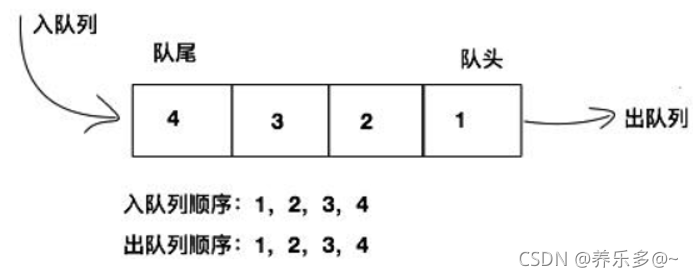
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
在实际生活中使用的地方也特别多如:银行办业务,取排队小票,按顺序办业务;超市结账,排队结账。
1.3 队列的实现
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数 组头上出数据,效率会比较低。
下面我们会用链表的形式来实现队列
1.3.1 队列的结构
队列的表现形式是链表形式,需要有存放地址指针域和值域
而队列本身有对头,对尾,和大小(方便入队列和出队列)
我们用两个结构体实现一个队列
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* next;
QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* front;
QNode* back;
int size;
}Queue;
1.3.2 队列的初始化
队列的初始化即让队列的头和尾先指向空,当我们入队列时从尾部入,出队列从头部出
// 初始化队列
void QueueInit(Queue* ps){
assert(ps);
ps->back = ps->front = NULL;
ps->size = 0;
}
1.3.3 入队列
入队列第一步需要开辟一个结点(用函数封装)
//创建新结点
QNode* buynode(QDataType data){
QNode* newnode = (QNode*)malloc(sizeof(QNode));
newnode->data = data;
newnode->next = NULL;
return newnode;
}
从队尾入
注意:当入第一个元素时,需要将第一个元素当做对头和队尾,之后就不需要了
// 队尾入队列
void QueuePush(Queue* ps, QDataType data){
assert(ps);
QNode* newnode = buynode(data);
if (ps->front == NULL){
ps->front = newnode;
}
else{
ps->back->next = newnode;
}
ps->back = newnode;
ps->size++;
}
1.3.4 出队列
注意:出队列表示删除该元素,并非输出该元素
出队列需要判断队列是否为空(用函数封装)
对头指向空即为空队列
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* ps){
assert(ps);
return NULL == ps->front;
}
对头出
先判断是否为空队列
要用一个指针保存对头,否则直接释放对头将找不到对头的下一个元素
// 队头出队列
void QueuePop(Queue* ps){
assert(ps);
if (QueueEmpty(ps)){
return;
}
else{
QNode* delNode = ps->front;
ps->front = delNode->next;
free(delNode);
if (NULL == ps->front)
{
ps->back = NULL;
}
}
ps->size--;
}
1.3.5 获取队列头部或队尾
只需将对头或队尾的值域输出即可(需要用print输出或者用变量接收)
需要持续输出对头的话搭配出队列交替使用
// 获取队列头部元素
QDataType QueueFront(Queue* ps){
assert(!QueueEmpty(ps));
return ps->front->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* ps){
assert(!QueueEmpty(ps));
return ps->back->data;
}
1.3.6 获取队列有效元素个数
空队列时会中止程序,可改为if(不终止)
// 获取队列中有效元素个数
int QueueSize(Queue* ps){
assert(!QueueEmpty(ps));
return ps->size;
}
1.3.7 销毁队列
依次释放头部指针
// 销毁队列
void QueueDestroy(Queue* ps){
assert(ps);
QNode* cur = ps->front;
while (cur){
ps ->front= cur->next;
free(cur);
cur = ps->front;
}
ps->back = NULL;
ps->size = 0;
}