[数据结构与算法]【LeetCode】376 and 733

376.摆动序列

解法1：动态规划
上升摆动序列最长子序列长度数组up，下降摆动序列最长子序列长度数组down。其中up[i]表示nums[0:i]的最长上升摆动子序列长度。同理，down[i]表示nums[0:i]的最长下降摆动子序列长度。更新公式：
若nums[i] > nums[i-1]，up[i] = max(up[i-1], down[i-1]+1)，down[i] = down[i-1]
若nums[i] < nums[i-1]，up[i] = up[i-1]，down[i] = max(down[i-1], up[i-1]+1)

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2:
            return n
        
        up = [1] + [0] * (n - 1)
        down = [1] + [0] * (n - 1)
        for i in range(1, n):
            if nums[i] > nums[i - 1]:
                up[i] = max(up[i - 1], down[i - 1] + 1)
                down[i] = down[i - 1]
            elif nums[i] < nums[i - 1]:
                up[i] = up[i - 1]
                down[i] = max(up[i - 1] + 1, down[i - 1])
            else:
                up[i] = up[i - 1]
                down[i] = down[i - 1]
        
        return max(up[n - 1], down[n - 1])

时间复杂度：O(n)
空间复杂度：O(n)
解法2：优化动态规划
由于当前状态只与前一状态有关，因此我们无需额外存储前一状态之前的状态信息，

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2:
            return n
        
        up = down = 1
        for i in range(1, n):
            if nums[i] > nums[i - 1]:
                up = down + 1
            elif nums[i] < nums[i - 1]:
                down = up + 1
        
        return max(up, down)

空间复杂度由O(n)降为O(1)
解法3：贪心
序列中的某个元素被称为「峰」，当且仅当该元素两侧的相邻元素均小于它。如序列 [1,3,2,4] 中，3 就是一个「峰」。
序列中的某个元素被称为「谷」，当且仅当该元素两侧的相邻元素均大于它。如序列 [1,3,2,4] 中，2 就是一个「谷」。
特别地，对于位于序列两端的元素，只有一侧的相邻元素小于或大于它，我们也称其为「峰」或「谷」。如序列 [1,3,2,4]中，1 也是一个「谷」，4 也是一个「峰」。
两个峰之间必定有谷，同理两个谷之间必定有峰。因此统计数组中峰谷的数量即为摆动序列的最大长度。

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2:
            return n
        
        prevdiff = nums[1] - nums[0]
        ret = (2 if prevdiff != 0 else 1)
        for i in range(2, n):
            diff = nums[i] - nums[i - 1]
            if (diff > 0 and prevdiff <= 0) or (diff < 0 and prevdiff >= 0):
                ret += 1
                prevdiff = diff
        
        return ret

时间复杂度：O(n)
空间复杂度：O(1)

733. 图像渲染

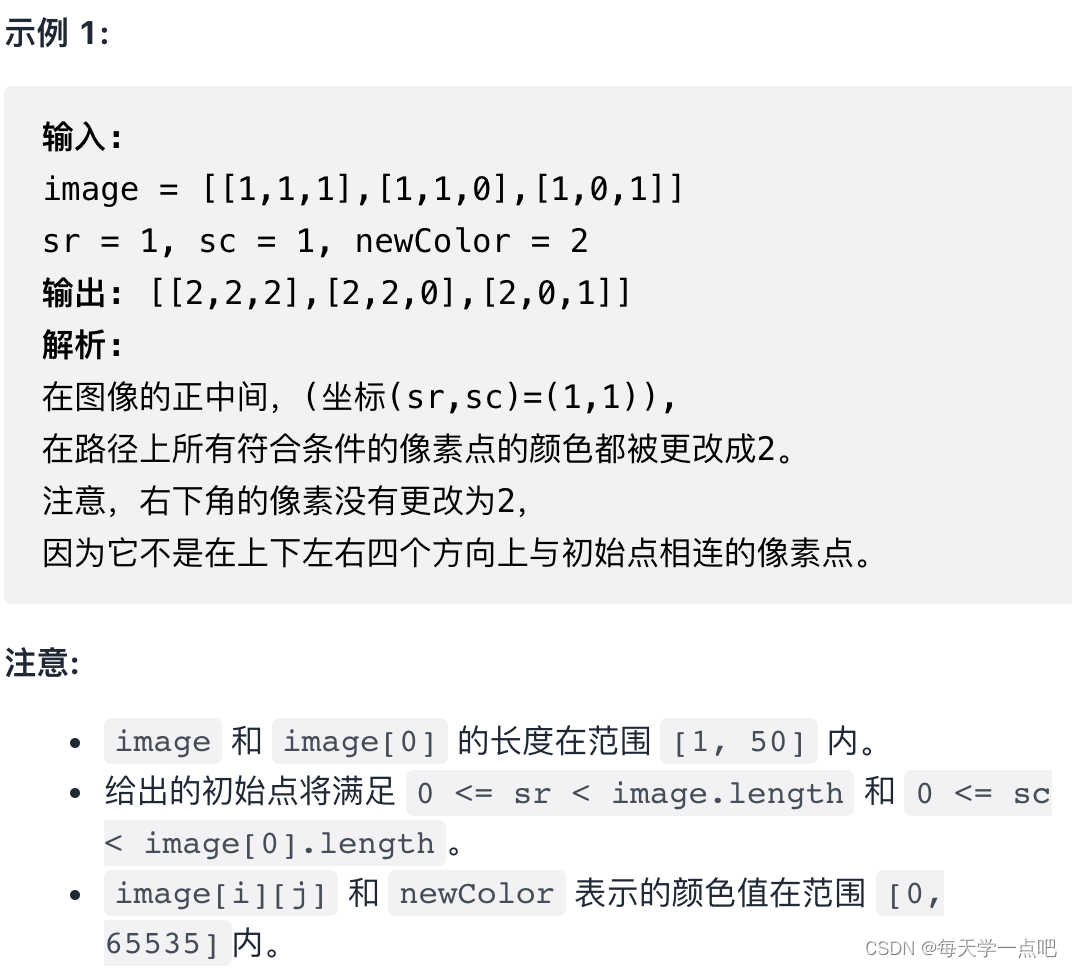
解法：DFS/BFS
我们从给定的起点开始，进行深度优先搜索。每次搜索到一个方格时，如果其与初始位置的方格颜色相同，就将该方格的颜色更新，以防止重复搜索；如果不相同，则进行回溯。
注意：因为初始位置的颜色会被修改，所以我们需要保存初始位置的颜色，以便于之后的更新操作。

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        n, m = len(image), len(image[0])
        currColor = image[sr][sc]

        def dfs(x: int, y: int):
            if image[x][y] == currColor:
                image[x][y] = newColor
                for mx, my in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                    if 0 <= mx < n and 0 <= my < m and image[mx][my] == currColor:
                        dfs(mx, my)

        if currColor != newColor:
            dfs(sr, sc)
        return image

时间复杂度：O(nxm)
空间复杂度：O(nxm)