
📢 大家好,我是小丞同学,一名大二的前端爱好者
📢 这篇文章将讲解数据结构中的堆
📢 非常感谢你的阅读,不对的地方欢迎指正 🙏
📢 愿你忠于自己,热爱生活
欢迎大家关注本专栏,持续关注最新文章~
本专栏的其他内容
从这里开始 👉 【化解数据结构】从这里开启数据结构和算法
队列 👉【化解数据结构】详解队列,优先队列,循环队列,并实现一个队列
💡 知识点抢先看
- 什么是堆?
- 如何实现一个堆结构?
- 手写实现一个堆结构
- LeetCode 实战
📢碎碎念
在上一篇文章中,我们学习了树结构,它是一个非顺序结构,接下来我们再来学习一个非顺序结构堆
一、什么是堆结构?
你可能会知道在内存中有栈和堆之分,但是这里堆和内存中的堆不一样,这里的堆是一种数据存储的方式
堆实际上是一种特殊的队列:优先队列,关于优先队列在队列文章中已经有讲过。也就是队列中有很多待执行的任务,执行时会根据优先级来执行,优先级高的会先被执行
这也可以很容易理解,比如医院急诊室里就有对病患的优先级之分,医生会优先处理病情严重的患者,再处理相较弱的患者
对于堆而言它是一种抽象的数据结构,或者说逻辑上的数据结构,并不是物理上真实存在的数据结构
在这里我们主要讨论的是二叉堆这种最常见的结构,它是用一棵完全二叉树来实现的
对于二叉树,我们在上一篇也有涉及,它是采用数组来实现的
因此二叉堆实际也是使用数组来实现的
那么什么是完全二叉树呢?
完全二叉树和满二叉树又类似,我们先来看看什么是满二叉树
1. 满二叉树
树中除了叶子节点,每个节点都有两个子节点
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
因此对于满二叉树的节点而言,它的度要么是 0,要么是 2,也就是要么有 2 个子节点,要么是叶子节点
如图就是一个满二叉树
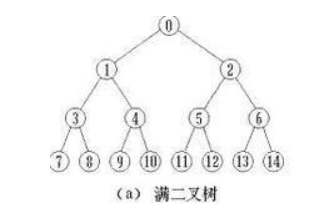
2. 完全二叉树
在满二叉树的性质上,最后一层的叶子节点,均在左树上
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
如图一棵完全二叉树
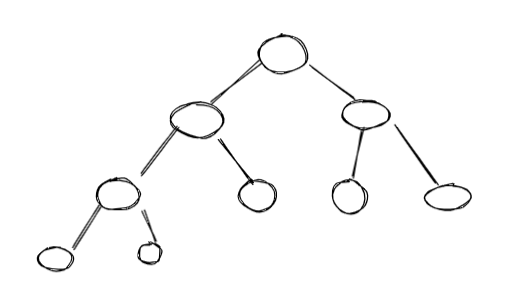
它们的区别:
- 完全二叉树最后一层没有满
- 满二叉树一定是完全二叉树
- 完全二叉树不一定是满二叉树
3. 堆的特点
好了了解了什么是完全二叉树,那堆有什么特点呢?
- 堆是一棵完全二叉树
- 任意节点都优于它的所有子节点
- 如果任意节点都大于它的所有子节点,那么它叫做最大堆,也叫大顶堆
- 如果任意节点都小于它的所有子节点,那么它叫做最小堆,也叫小顶堆
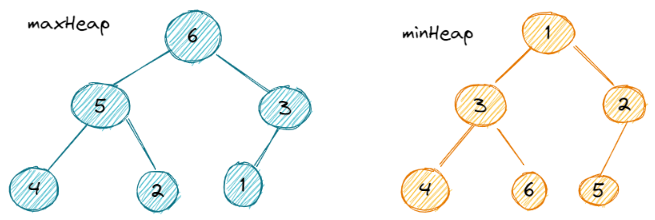
左边是一个最大堆,所有的子节点都小于父节点
二、如何能够实现一个堆结构呢?
在 JS 中通过数组来实现一个堆结构,其实本质就是一个数组。在上一篇文章结尾也说了,无论什么数据结构,在内存中都只是数组,或者对象罢了,所有的数据结构都是我们心中存在的,我们知道这么做的好处是怎么怎么样
在这里选用数组来实现一个堆
利用广度优先遍历,将树填入数组里,这样我们就能用一个数组来表示一个堆了
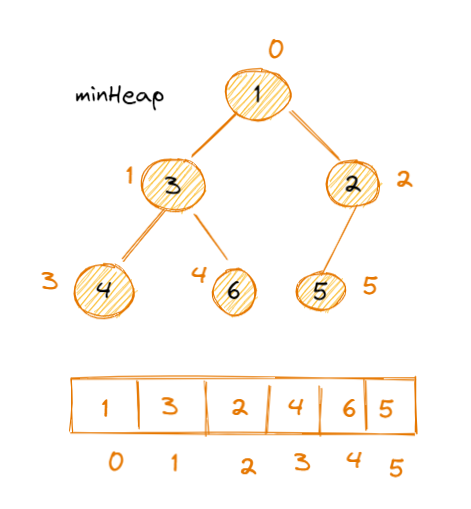
小秘诀
- 左侧子节点在数组中的位置是
2 * index + 1 - 右侧子节点在数组中的位置是
2 * index + 2 - 父节点的位置是
(index - 1) / 2
因此我们不仅能够使用数组来表示一个堆,我们还能获取任意一个节点在数组中的位置,接下来我们就实现一个最小堆
三、堆中有哪些方法?
我们给堆添加一些方法,一遍它在插入时,能插到准确的位置,删除时,其他的元素也能进行合理的移动
| 方法 | 含义 |
|---|---|
swap() | 交换两个数 |
getParentIndex(i) | 获取 i 的父节点 |
getLeftIndex(i) | 获取 i 的左子节点 |
getRightIndex(i) | 获取 i 的右子节点 |
shirtUp(i) | 上移操作 |
shirtDown(i) | 下移操作 |
insert(value) | 插入值 |
pop() | 删除堆顶 |
peek() | 获取堆顶 |
size() | 获取堆的大小 |
四、手写实现一个最小堆
在前面我们已经知道了最小堆的定义,它的所有节点都小于等于它的子节点,因此我们根据这个特性,以及3个小秘诀来实现一个最小堆
1. 创建一个 MinHeap 类
利用数组来实现一个堆类
class MinHeap {
constructor() {
this.heap = []
}
}
2. 实现 swap 方法
我们需要维护一个堆结构,在元素插入删除的时候,常常需要进行位置的变化,因此我们需要通过交换位置来实现
封装一个 swap 方法,接收交换位置的两个节点
swap(i1, i2) {
const temp = this.heap[i1]
[this.heap[i1], this.heap[i2]] = [this.heap[i2], temp]
}
在这里采用数组解构的方式来赋值,看着舒服一点
3. 实现 getParentIndex 方法
getParentIndex 方法获取某个节点父元素在数组中的位置
根据上面的小秘诀:父节点的位置是 (index - 1) / 2
在这里我们采用二进制的方式来取值
小课堂:你知道 JavaScript 中的
~~运算符是什么意思吗
getParentIndex(i) {
// 取商 (i- 1)/2 等同于 Math.floor((i-1)/2)
// 二进制数向右边移一位,这样刚好就是求商
return (i - 1) >> 1
}
4. 实现 getLeftIndex 方法
同样的根据秘诀:左侧子节点在数组中的位置是 2 * index + 1
getLeftIndex(i) {
return i * 2 + 1
}
5. 实现 getRightIndex 方法
右侧子节点在数组中的位置是 2 * index + 2
getRightIndex(i) {
return i * 2 + 2
}
6. 实现 shirtUp 方法
这个方法是实现最小堆的关键之一,在我们插入元素时,需要对元素进行判断,我们需要将插入的元素移到符合它的位置
如何实现呢?采用递归
- 首先我们需要先判断节点的位置是否在堆的顶部,这也是递归结束的标记之一
- 接下来进行递归体的内容,我们递归实现的目的是通过交换使元素到达合适位置
- 因此判断插入元素和父节点的值关系,如果父节点的值大于当前节点值,则进行上移(因为最小堆,小的在堆顶)
- 直至递归结束
shirtUp(index) {
// 如果在堆顶,停止上移
if(index == 0) return
// 获取父元素
const parentIndex = this.getParentIndex(index)
// 比较
if (this.heap[parentIndex] > this.heap[index]) {
// 交换
this.swap(parentIndex, index)
// 递归
this.shirtUp(parentIndex)
}
}
7. 实现 insert方法
在写好了上移 shirtUp 方法,我们就可以实现 insert 方法来看看我们实现的效果了
insert 方法的作用是插入一个元素,在堆中插入一个元素之后,我们需要通过 shirtUp 方法来将这个元素移到合适的位置,这个操作留给 shirtUp 方法来解决
注意哦,
shirtUp方法接收的是index,也就是索引值
insert(value) {
this.heap.push(value)
this.shirtUp(this.heap.length - 1)
}
来看看在一个堆中插入元素是如何运作的吧,这是一个最大堆中的动图,最小堆也一样
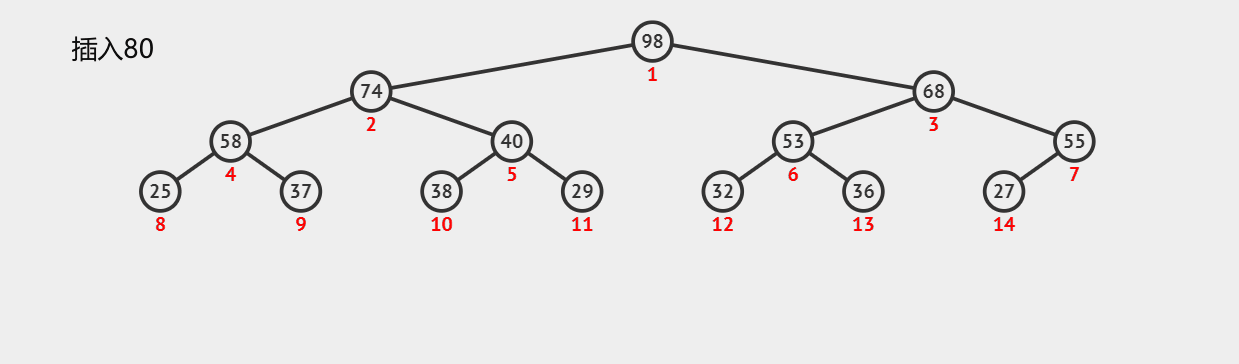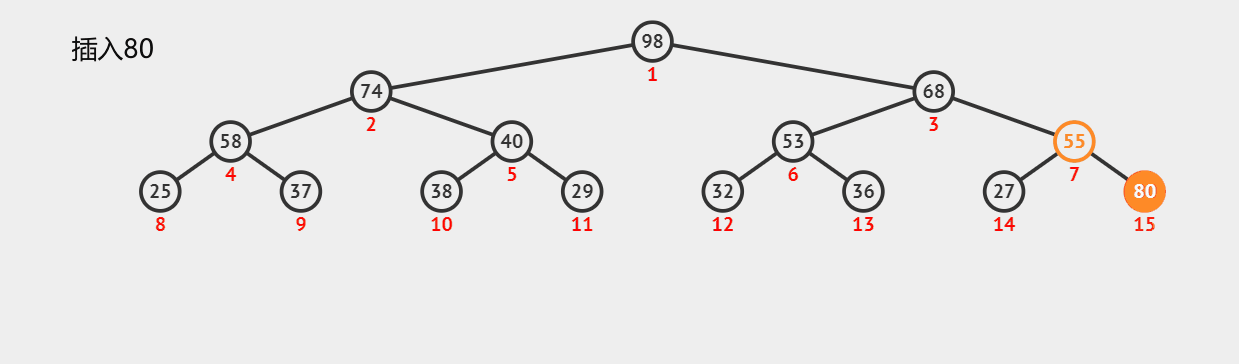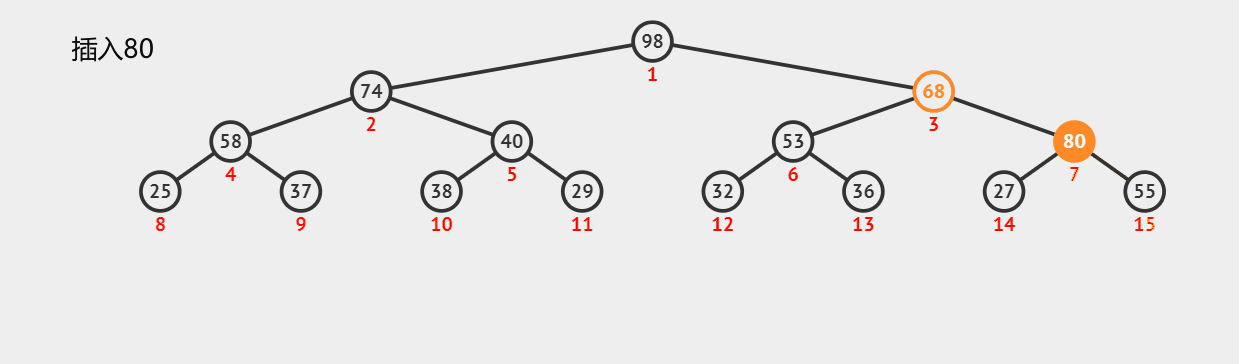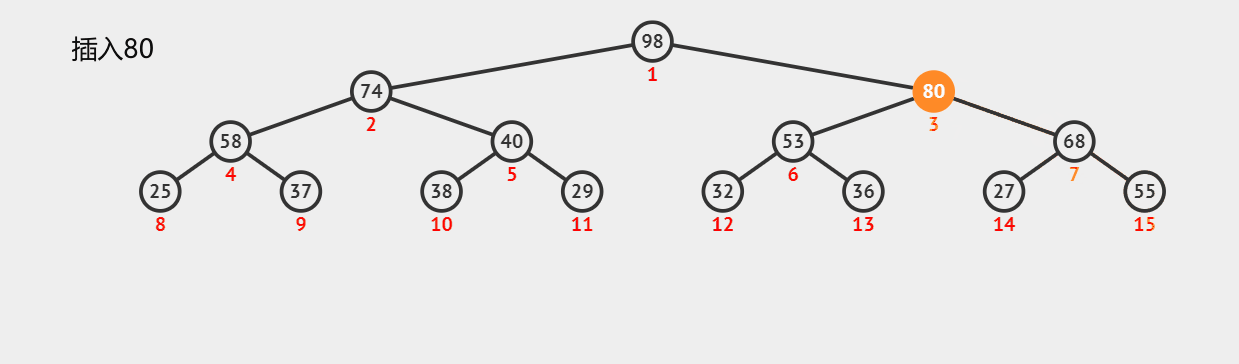
时间复杂度是多少你知道吗?
O(logK)
8. 实现 pop 方法
为什么需要有下移的方法,当我们直接删除堆顶时,会导致整个堆的结构的变化,使得大小关系转变,难以操作
因此我们在删除堆顶时,只需要用数组尾部的元素,替换堆顶元素,这样改变的就只有首尾两个元素,我们再对堆顶进行下移判断,这样通过不断地交换,就能实现最小堆
pop() {
// 用最后一个替换堆顶
this.heap[0] = this.heap.pop()
// 再下移
this.shirtDown(0)
}
9. 实现 shirtDown 方法
接下来我们实现最为关键的下移代码,如何实现呢?
- 和左右子节点进行比较
- 左子节点小于当前节点,交换,继续递归
- 右子节点小于当前节点,交换,递归
shirtDown(index) {
const leftIndex = this.getLeftIndex(index)
const rightIndex = this.getRightIndex(index)
// 左侧子节点小于当前节点
if (this.heap[leftIndex] < this.heap[index]) {
this.swap(leftIndex, index)
this.shirtDown(leftIndex)
}
// 右侧子节点小于当前节点
if (this.heap[rightIndex] < this.heap[index]) {
this.swap(rightIndex, index)
this.shirtDown(rightIndex)
}
}
我们来看看删除堆顶时会发生什么?
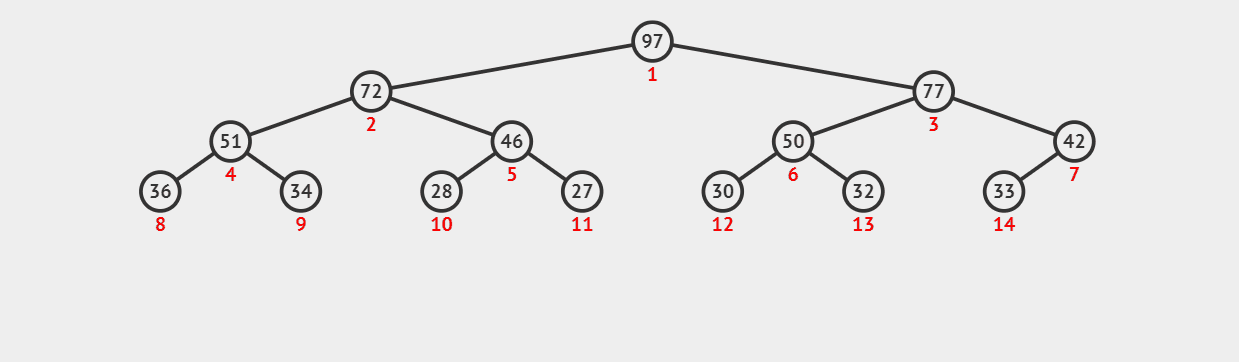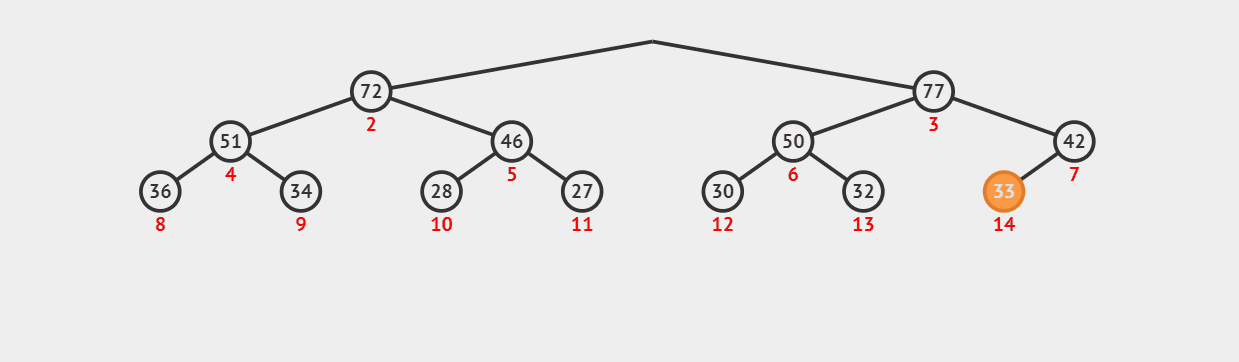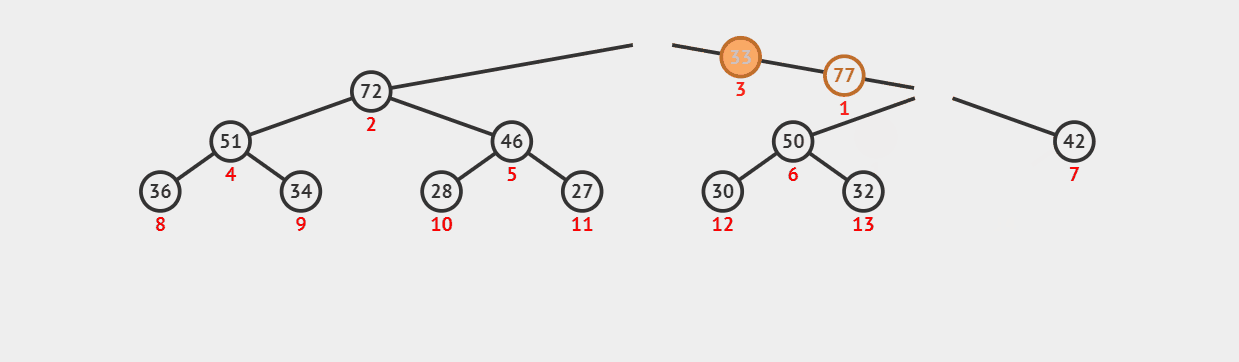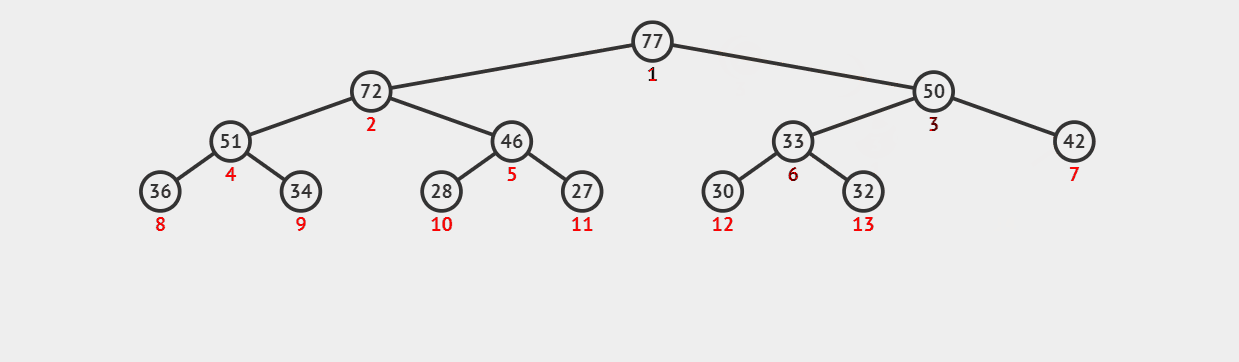
10. 实现 peek 方法
返回堆顶元素,也就是堆的最小值,数组的第一位
peek() {
return this.heap[0]
}
11. 实现 size 方法
最后,实现最简单的方法,通过数组的 length 来获取即可
size() {
return this.heap.length
}
12. 完整的 MinHeap 类
// 写一个最小堆
class MinHeap {
constructor() {
this.heap = []
}
// 获取父节点
getParentIndex(i) {
// 取商 (i- 1)/2 等同于 Math.floor((i-1)/2)
// 二进制数向右边移一位,这样刚好就是求商
return (i - 1) >> 1
}
// 获取左节点
getLeftIndex(i) {
return i * 2 + 1
}
getRightIndex(i) {
return i * 2 + 2
}
// 交换两个数的方法
swap(i1, i2) {
const temp = this.heap[i1]
[this.heap[i1], this.heap[i2]] = [this.heap[i2], temp]
}
// 上移操作,最小堆,小的要在最上面
shirtUp(index) {
// 如果在堆顶,停止上移
if (index == 0) return
const parentIndex = this.getParentIndex(index)
if (this.heap[parentIndex] > this.heap[index]) {
this.swap(parentIndex, index)
this.shirtUp(parentIndex)
}
}
// 下移操作
shirtDown(index) {
const leftIndex = this.getLeftIndex(index)
const rightIndex = this.getRightIndex(index)
// 左侧子节点小于当前节点
if (this.heap[leftIndex] < this.heap[index]) {
this.swap(leftIndex, index)
this.shirtDown(leftIndex)
}
// 右侧子节点小于当前节点
if (this.heap[rightIndex] < this.heap[index]) {
this.swap(rightIndex, index)
this.shirtDown(rightIndex)
}
}
// 插入 O(logK)
insert(value) {
this.heap.push(value)
this.shirtUp(this.heap.length - 1)
}
// 删除堆顶
pop() {
// 用最后一个替换堆顶
this.heap[0] = this.heap.pop()
// 再下移
this.shirtDown(0)
}
// 获取堆顶
peek() {
return this.heap[0]
}
// 获取大小
size() {
return this.heap.length
}
}
五、LeetCode 实战
在前端世界中,堆也有它的应用场景,它能够高效的找到最大值,最小值,时间复杂度为 O(1),
利用堆结构,我们可以轻松解决找出最大、最小元素、第 K 大元素登问题,但远不止于这些
几道 LeetCode 中关于堆的题目
215. 数组中的第K个最大元素
347. 前 K 个高频元素
1046. 最后一块石头的重量
703. 数据流中的第 K 大元素
📖 总结
在这篇文章中我们详细讲解了,什么是一个堆,如何实现一个堆,到最后手写封装了一个最小堆,在这过程中我们知道了如何将一个元素插入堆中,如何获取堆中的特定元素。
在我们实际的堆应用当中,或者算法题当中,不一定需要将整个堆结构都实现,我们只需要实现特定的部分就可以了,不然光封装一个堆的时间都够一壶茶了,因此学习数据结构和算法,我们更多的是学习它里面的思想,对于一个堆,不过只是 “数组”而已
本文关于堆的内容就到这里结束了,相信你一定能从中学到很多东西。下一篇文章将带你探索图的奥秘。
最后,可能在很多地方讲诉的不够清晰,请见谅
💌 如果文章有什么错误的地方,或者有什么疑问,欢迎留言,也欢迎私信交流