文章目录
栈
概念及结构
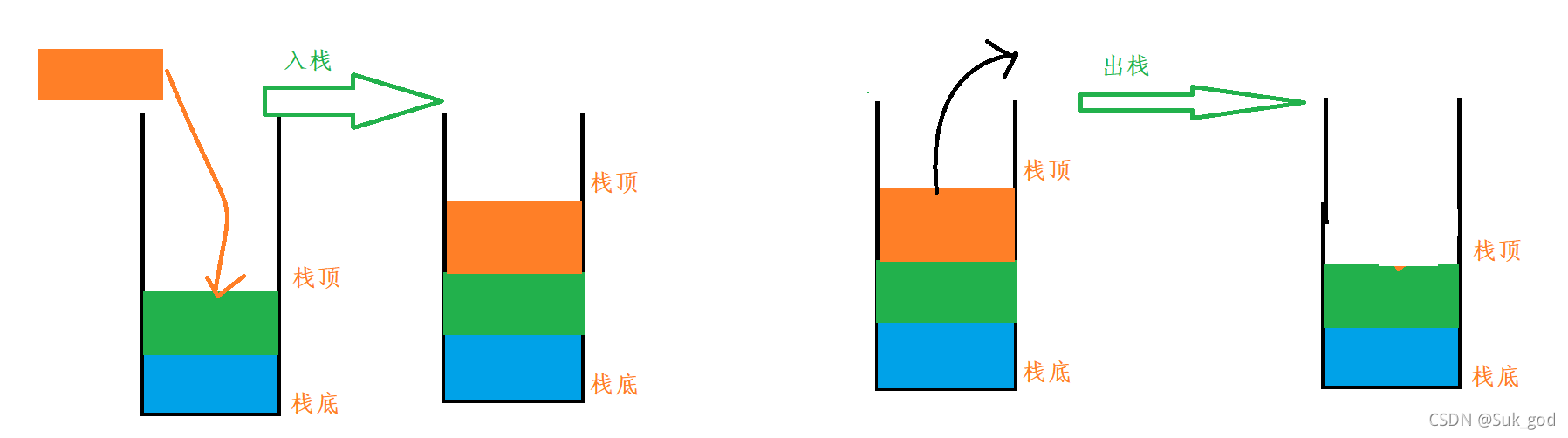
一种特殊的线性表,只能在固定的一端进行插入和删除操作,进行插入和删除的一端称为栈顶,另一端称为栈底。
数据元素遵循:后进先出,LIFO(Last in first out);
压栈(入栈):插入数据的过程
出栈:删除栈顶元素的过程。
栈的实现
结构的选择
栈可以使用顺序表或者链表来实现,考虑到栈的操作来说,顺序表的结构实现更优一些。因为在数组末尾插入数据代价较小。
因此:选用顺序表来实现栈这一数据结构
分类
静态栈结构
实际上这种结构并不实用,所以不推荐使用。
typedef int STDataType;
#define N 10
typedef struct Stack
{
STDataType a[N];//数组大小提前给定了
int top; // 栈顶
}Stack;
动态的栈结构
动态增长的栈,相对比较实用,用户可以根据情况确定使用栈的空间大小。
typedef int STDataType;
typedef struct Stack
{
STDataType* array;
int top; // 栈顶
int capacity; // 容量
}Stack;
动态增长的栈相关操作实现
1.栈的基本结构定义
#define DEFAULT 3
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* arr;
int top; // 栈顶
int capacity; // 容量
}Stack;
2.初始化栈
对于栈的初始化,我们只需要为其开辟空间(使用malloc从堆上申请),然后将栈顶top置为0,也就是处于数组的第一个空间位置处。
void StackInit(Stack* ps)
{
ps->arr = (STDataType*)malloc(sizeof(STDataType)* DEFAULT);
if (NULL == ps->arr)
{
assert(0);
return;
}
ps->capacity = DEFAULT;
ps->top = 0;
}
3.栈的销毁
由于初始化时数组的空间是从堆上开辟的,所以在使用完毕之后需要释放申请的内存空间,否则会发生内存泄漏。
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
if (ps->arr)
{
free(ps->arr);
ps->arr = NULL;
ps->capacity = 0;
ps->top = 0;
}
}
判断栈是否为空
只需要判断top的值是否为0,若为0,则栈空,否则不空~
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{
assert(ps);
return 0 == ps->top;
}
入栈操作
数据入栈,只需要将数据插入到top所在的位置,然后将top加1。
但是:会不会出现无法插入的情况???
会的,如果栈空间满了,就无法开辟进行入栈操作
怎么办??当然是扩容之后再入栈了~~
如何扩容呢?
有以下几步构成:
1、重新开辟空间
2、将旧空间的元素copy到新空间
3、释放旧空间
4、使用新空间
具体操作见代码
扩容
static void CheckCapicity(Stack* ps)
{
if (ps->top == ps->capacity)
{
//1.申请新空间
int newCapicity = ps->capacity * 2;
STDataType* newArr = (STDataType*)malloc(sizeof(STDataType)*newCapicity);
if (NULL == newArr)
{
assert(0);
return;
}
//2.拷贝元素
memcpy(newArr, ps->arr, sizeof(STDataType)*ps->top);
//3.释放旧空间
free(ps->arr);
//4.使用新空间
ps->arr = newArr;
ps->capacity = newCapicity;
}
}
入栈
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
CheckCapicity(ps);
ps->arr[ps->top] = data;
ps->top++;
}
出栈
出栈就不需要考虑那么多了,只需要判断一下栈是否为空,若不空,让top–就可以实现出栈操作。(top–后尽管要出栈元素依然存在,但是已经无法访问到)
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
if (!StackEmpty(ps))
{
ps->top--;
}
}
获取栈顶元素
1、判断栈是否为空
2、若不空,去array[top-1]处的元素即为栈顶元素
注意:取栈顶元素与出栈不同,不需要改变top自身的值
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(!StackEmpty(ps));
return ps->arr[ps->top-1];
}
获取栈中元素个数
top:既表示栈顶,也表示有效元素的个数
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;
}
测试代码
void testStack()
{
Stack s;
StackInit(&s);
StackPush(&s, 1);
StackPush(&s, 2);
StackPush(&s, 3);
StackPush(&s, 4);
StackPush(&s, 5);
int num = StackTop(&s);
int size = StackSize(&s);
printf("%d %d\n",num,size);
StackPop(&s);
StackPop(&s);
StackPop(&s);
int num1 = StackTop(&s);
int size1 = StackSize(&s);
printf("%d %d\n", num1, size1);
StackDestroy(&s);
}
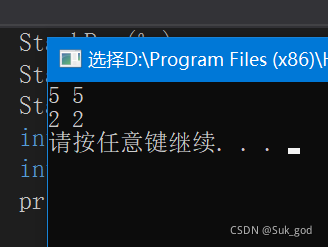
输出结果:
队列
概念及结构
只允许在一端进行数据插入操作,另一端进行数据删除操作的线性结构。
队头:进行数据删除的一端
队尾:进行数据插入的一端
队列特点:先进先出
队列的实现
结构的选择
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
因此,选用链表来实现队列
相关操作的实现
数据结构的定义
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* next;
QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* front;
QNode* rear;
int size;//队列里有效元素个数
}Queue;
队列的初始化
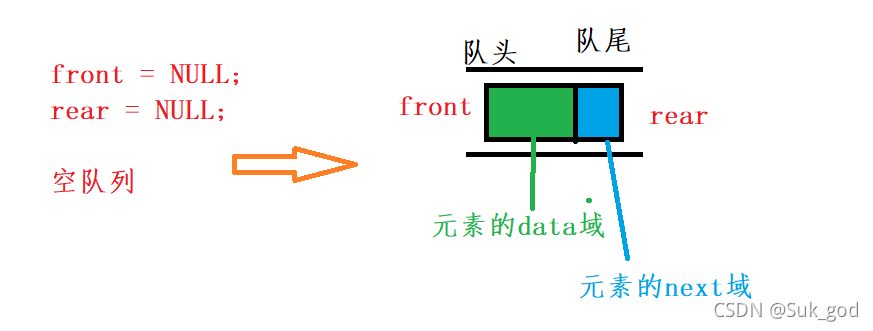
刚开始,队列没有元素,只需要申请一个空队列,即front和rear都置为NULL,size置为0
//申请一个节点
QNode* buyQNode(QDataType data)
{
QNode* Node = (QNode*)malloc(sizeof(QNode));
if (NULL == Node)
{
assert(0);
return NULL;
}
Node->data = data;
Node->next = NULL;
return Node;
}
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->front = q->rear = NULL;
q->size = 0;
}
销毁队列
对于队列的销毁,我们只需要循环遍历整个队列,采用“单链表头删”的方式进行释放,直到将整个队列全部释放。
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* delNode = q->front;
while (q->front)
{
q->front = delNode->next;
free(delNode);
delNode = q->front;
}
q->rear = NULL;
q->size = 0;
}
判断队列是否为空
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
return NULL == q->front;
}
入队操作
1.队列为空
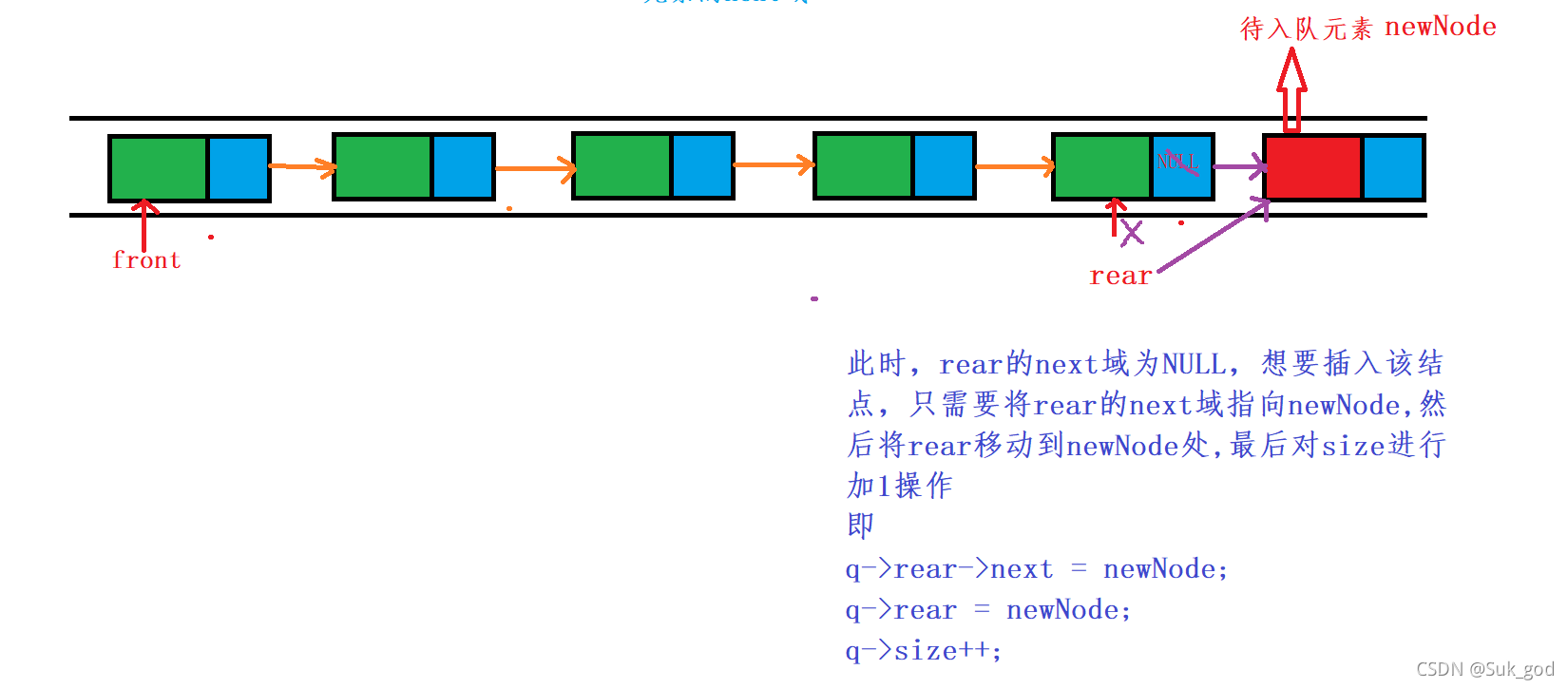
2.队列不空
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newNode = buyQNode(data);
//1.队列为空
if (NULL == q->front)
{
q->front = newNode;
}
//2.队列不空
else
{
q->rear->next = newNode;
}
q->rear = newNode;
q->size++;
}
出队操作
如果队列不空,就可以执行出队列操作,否则直接返回
1.队列有多个结点
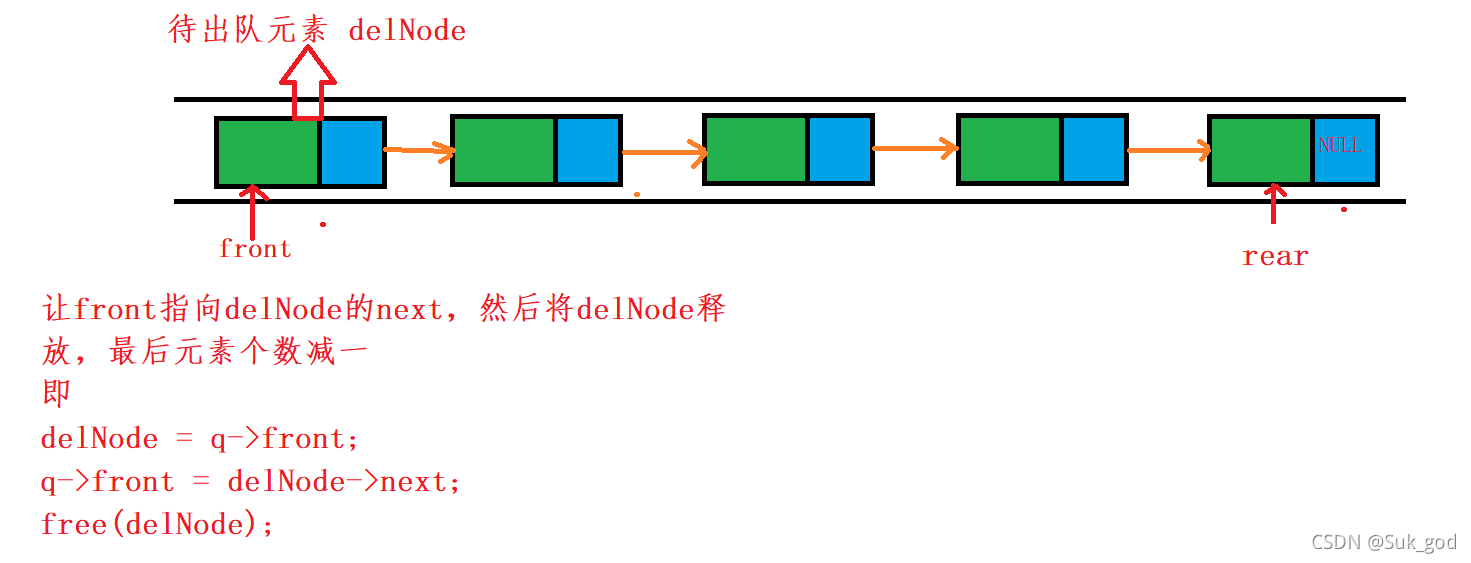
2.队列只有1个元素
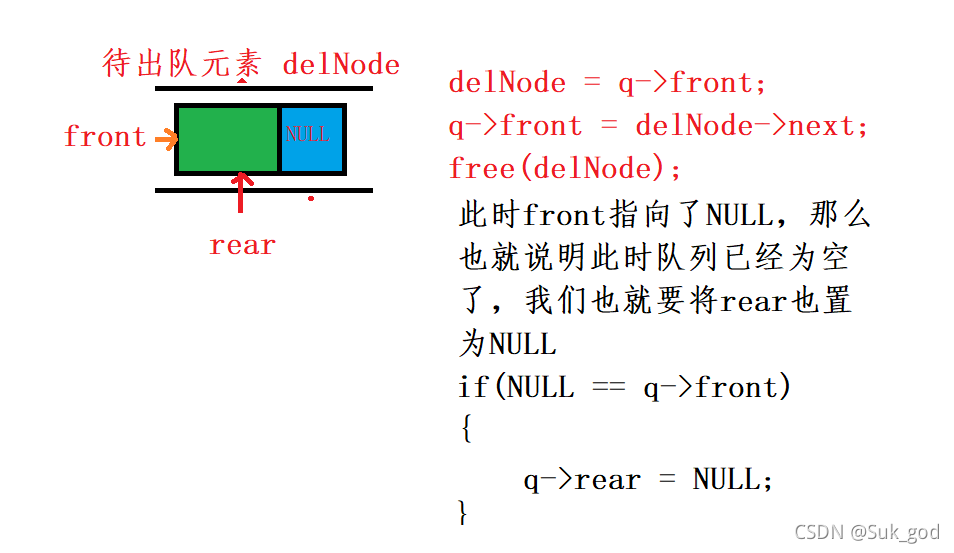
// 队头出队列
void QueuePop(Queue* q)
{
if (QueueEmpty(q))
{
return;
}
else
{
QNode* delNode = q->front;
q->front = delNode->next;
free(delNode);
if (q->front == NULL)
{
q->rear = NULL;
}
q->size--;
}
}
获取队头元素
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(!QueueEmpty(q));
return q->front->data;
}
获取队尾元素
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(!QueueEmpty(q));
return q->rear->data;
}
获取有效元素个数
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
测试代码
void testQueue()
{
Queue q;
QueueInit(&q);
QueuePush(&q, 1);
QueuePush(&q, 2);
QueuePush(&q, 3);
QueuePush(&q, 4);
QueuePush(&q, 5);
printf("队头:%d 队尾:%d 有效元素个数:%d \n", QueueFront(&q), QueueBack(&q), QueueSize(&q));
QueuePop(&q);
QueuePop(&q);
QueuePop(&q);
QueuePop(&q);
printf("队头:%d 队尾:%d 有效元素个数:%d \n", QueueFront(&q), QueueBack(&q), QueueSize(&q));
QueueDestroy(&q);
}
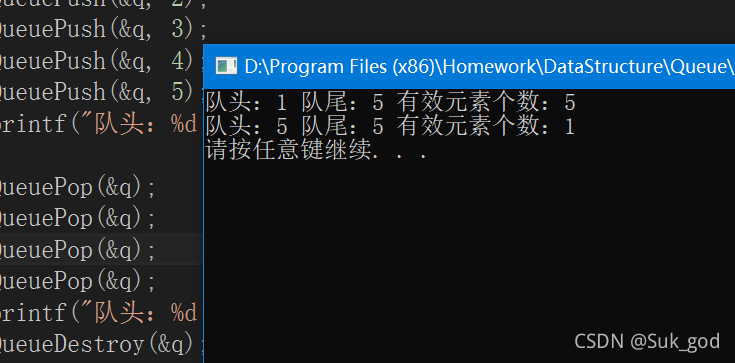
以上就是对栈和队列基础操作的分享,各位看官们请留下你们的足迹~~