[数据结构与算法]leetcode105/1382-构建二叉树与二叉平衡树（人生苦短，速速递归）

构建二叉树

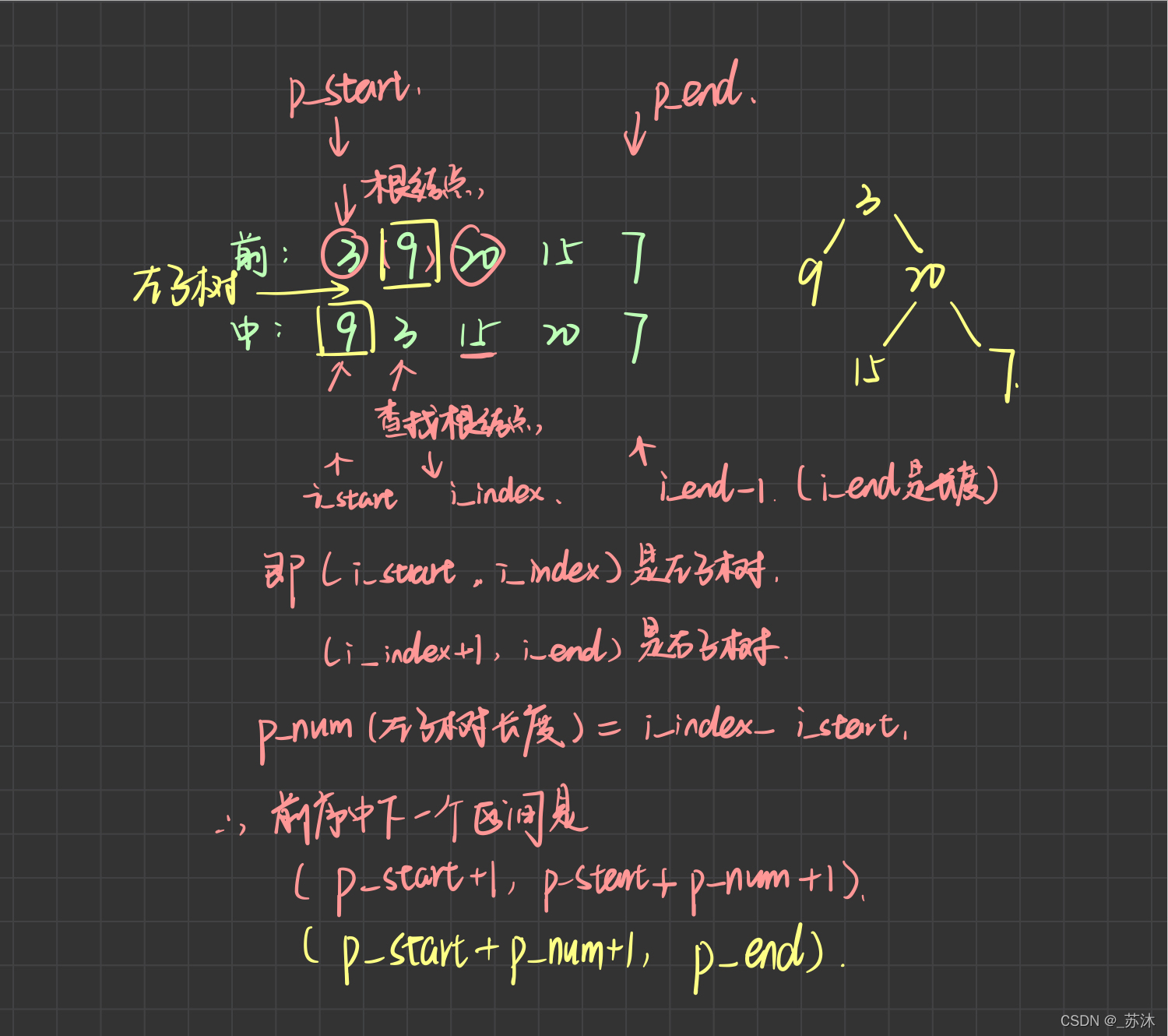
前序序列与中序序列 共同构建二叉树：
1??遍历前序序列，找到第一个即为根结点
2??去中序序列中找相应的结点，该结点左侧即为左子树，右侧即为右子树🌲
3??递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* dfs(int preorder[],int p_start,int p_end,int inorder[],int i_start,int i_end)
{
    if(p_start == p_end)
        return NULL;
    int root = preorder[p_start];
    int i_index;
    for(int i = i_start;i < i_end;i++)
    {
        if(inorder[i] == root)
        {
            i_index = i;
            break;
        }
    }
    int p_num = i_index-i_start;
    struct TreeNode* t = (struct TreeNode*)malloc(sizeof(struct TreeNode)*1);
    t->val = root;
    t->left = dfs(preorder,p_start+1,p_start+p_num+1,inorder,i_start,i_index);
    t->right = dfs(preorder,p_start+p_num+1,p_end,inorder,i_index+1,i_end);
    return t;
}
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    return dfs(preorder,0,preorderSize,inorder,0,inorderSize);
}

将二叉搜索树变平衡
1??先将给出的二叉搜索树 存入数组
2??将数组对应创建平衡树🌲
3??递归
存入数组的过程就是一个遍历的过程，熟练掌握；
然后每次取数组中间的树作为结点，创建二叉树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* dfs(int returns[],int low,int high)
{
    if(low > high)
    {
        return NULL;
    }
    int mid = (low + high)/2;
    struct TreeNode *t = (struct TreeNode* )malloc(sizeof(struct TreeNode)*1);
    t->val = returns[mid];
    t->left = dfs(returns,low,mid-1);
    t->right = dfs(returns,mid+1,high);
    return t;
}

void visit(struct TreeNode* root,int returns[],int *returnSize)
{
    if(root == NULL)
        return;
    visit(root->left,returns,returnSize);
    returns[(*returnSize)++] = root->val;
    visit(root->right,returns,returnSize);
    // return root;
}

struct TreeNode* balanceBST(struct TreeNode* root){
    //先遍历 存储到一个数组中，将整棵树 以一个 升序序列存放
    // struct TreeNode* returns = (struct TreeNode* )malloc(sizeof(struct TreeNode)*10010);
    int *returns = (int *)malloc(sizeof(int)* 10010);
    int returnSize = 0;
    visit(root,returns,&returnSize);
    //再以中间建立 二叉搜索平衡树
    return dfs(returns,0,returnSize-1);
    // printf("%d",returnSize);
    // for(int i = 0;i < returnSize;i++)
    // {
        // printf("%d",returns[i]);
    // }
    
    // return root;
}