[数据结构与算法]主成分分析(PCA)

主成分分析(PCA)

1 概念

主成分是选出比原始变量个数少，能解释大部分资料中的变异的几个新变量

主成分分析是考察多个变量间相关性一种多元统计方法，通过较少的变量(几个主成分)来解释多个变量间的内部结构，即从原始变量中导出少数几个主分量，使它们尽可能多地保留原始变量的信息，且彼此间相互独立（互不相关）

主成分分析--->数据降维

常被用来寻找判断事物或现象的综合指标，并对综合指标所包含的信息进行适当的解释

2 基本思想

设法将原来众多具有一定相关性的变量(如p个变量)，重新组合成一组新的相互无关的综合变量来代替原始变量

将原来p个变量做线性组合作为新的综合变量

方差<--->信息量，即$var(F1)$越大，表示$F1$包含的信息越多，因此在所有的线性组合中所选取的$F1$应该是方差最大的，故称之为第一主成分

• 如果把两个变量用一个变量来表示，同时这一个新的变量又尽可能包含原来的两个变量的信息，这就是降维的过程
• 以两个变量X1和X2为例，找出的这些新变量是原来变量的线性组合，叫做主成分[Z=a1X1+a2X2]

主成分构造原则：

1. 在损失很少的数据信息的前提下，把多个因素指标利用正交旋转变换转换成几个综合指标（主成分）
2. 每个主成分都是原始变量的线性组合，且各个主成分之间相互独立（互不相关）

根据主成分的构造思想和(皮尔逊)相关系数公式，要使得综合变量之间不相关，则各自对应的方差应该越大越好

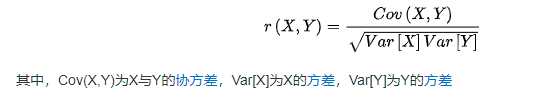
主成分选取原则【任一个满足即可】：

1. 各主成分的累积方差贡献率>80%?
2. 特征值$\lambda >1$

主成分性质：

1. 主成分$Z$的协方差阵为对角阵，且对角线元素为${\lambda }_1,{\lambda }_2,...,{\lambda }_p$
2. 记$\sum =({\sigma }_{ij})$，有$\sum _{i=1}^p{\lambda }_i=\sum _{i=1}^p{\sigma }_{ij}$，称$${\alpha }_i=\frac{{\lambda }_i}{\sum _{i=1}^p{\lambda }_i},i=1,2,...,p$$为第i个主成分的贡献率，称$$\frac{\sum _{i=1}^m{\lambda }_i}{\sum _{i=1}^p{\lambda }_i},i=1,2,...,p$$为前m个主成分的累积贡献率
3. 选取的主成分对原始变量的贡献值用相关系数的平方和来表示，若选取的主成分为$Z_1,Z_2,...,Z_m$，则它们对原始变量$X_i$的贡献值为$${\rho }_i=\sum _{k=1}^m{r}^2(Z_k,X_i)$$其中$r(Z_k,X_i)$为$Z_k$与$X_i$的相关系数

3 数学模型

假定有n个样本，每个样本共有p个变量(指标)，构成一个$n\times p$的数据矩阵

当$p$较大时，在$p$维空间中考察问题比较麻烦。为了克服这一问题，就需要进行降维处理，即用较少的几个综合变量代替原来较多的变量，而且使这些较少的综合变量能尽量多地反映原来较多变量所反映的信息

要从原来的所有变量得到新的综合变量，一种较为简单的方法是作线性变换，使新的综合变量为原始变量的线性组合

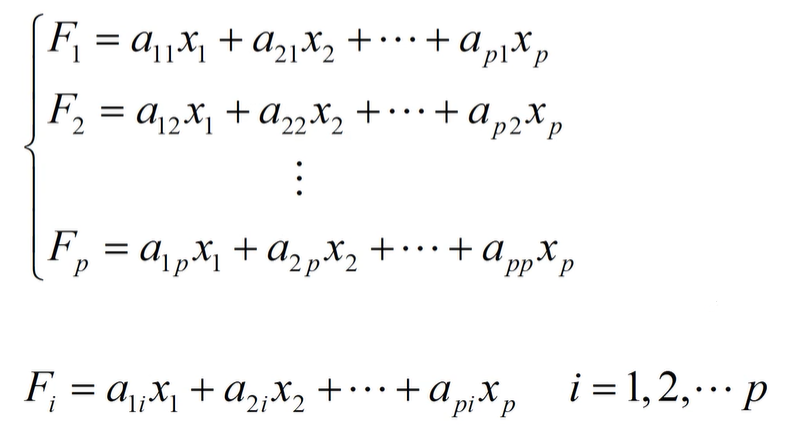
条件：

• 对于任意常数$c$，有$$\mathrm{var}(c{F}_i)=c^2\mathrm{var}(F_i)$$为了使方差$var(F_i)$可以比较，要求线性组合的系数满足规范化条件：$$a_{i1}^2+a_{i2}^2+a_{i3}^2+...+a_{ip}^2=1$$

• 要求原始变量之间存在一定相关性(相关系数分析判断)

• 要求各个综合变量间互不相关，即协方差为0

• 为了消除变量量纲不同对方差的影响，通常对数据进行标准化处理，变量之间的协方差即为相关系数

• 做不做主成分分析的两大检验(任一个满足即可)：

  

  1. KMO(Kaiser-Meyer-Olkin)检验：检验变量之间的偏相关系数是否过小【此值>0.5时可以作主成分分析】

  2. Bartlett's检验：检验显著性水平(Sig.)【此值<0.05时可以作主成分分析】

4 步骤

1. 对原来$p$个指标进行数据标准化处理，以消除变量在水平和量纲上的影响

2. 根据标准化后的数据矩阵求出相关系数矩阵(等同于协方差矩阵)

3. 求出协方差矩阵的特征根和特征向量

4. 确定主成分，并对各主成分所包含的信息给予适当的解释

5 主成分回归

主成分回分析(PCR)是为了克服最小二乘(LS)估计在数据矩阵A存在多重共线性时表现出的不稳定性而提出的，就是将主成分$Z_1，Z_2,...,Z_p$或选择部分作自变量，对$y$与$Z$之间建立回归模型的过程

基本思想：

将原来的回归自变量变换到另一组变量，即主成分，选择其中一部分重要的主成分作为新的自变量，丢弃了一部分影响不大的自变量，实际上达到了降维的目的，然后用最小二乘法对选取主成分后的模型参数进行估计，最后再变换回原来的模型求出参数的估计

目的：

• 解决当方程个数$n$<未知参数个数$p$时，最小二乘估计失效的问题
• 消减自变量之间的多重共线性

步骤：

1. 先进行主成分分析，确定主成分

2. 对主成分和因变量作最小二乘回归，得到主成分回归方程

3. 主成分变量的回归系数乘以特征向量，化成标准化变量的回归方程

4. 恢复为原始变量的主成分回归方程

6 PCR之Matlab实例

%% 主成分回归分析(PCR)
%% I.清空环境
clc,clear
close all
%% II.导入数据
load sn.txt
[m,n]=size(sn)
%% III.数据预处理
% 提取数据
x0=sn(:,[1:n-1])
y0=sn(:,n)

%% IV.最小二乘法回归(LSR)
% X是系数矩阵(第1列全是1+其余列是自变量) Y是因变量(列向量)
X=[ones(m,1),x0]
Y=y0
% 最小二乘法估计回归系数(最小二乘法的Matlab实现--左除\)
ls_hg=X\Y
ls_hg=ls_hg' % 行向量显示回归系数（第1分量是常数项）
% 显示最小二乘法回归结果
fprintf('最小二乘法回归方程：\n')
fprintf('y=%f',ls_hg(1))
for i=2:n
    if ls_hg(i)>0
        fprintf('+%f*x%d',ls_hg(i),i-1)
    else
        fprintf('%f*x%d',ls_hg(i),i-1)
    end
end
fprintf('\n')

%% V.主成分回归(PCR)
% 数据标准化处理
xd=zscore(x0)
yd=zscore(y0)
% 计算相关系数矩阵
r=corrcoef(xd)
% 计算协方差矩阵(相关系数矩阵)的特征向量(vec1)和特征值(lamda)以及各个主成分的贡献率(rate)
[vec1,lamda,rate]=pcacov(r)
% 计算累积贡献率，第i个分量表示前i个主成分的累积贡献率
contr=cumsum(rate)
% 构造与vec1同维数的元素为1和-1的矩阵
% sign：符号函数
% repmat(ones(1,4),4,1)：垂直堆叠行向量四次
f=repmat(sign(sum(vec1)),size(vec1,1),1)
% 修改特征向量的正负号，使得特征向量的所有分量和为正
vec2=vec1.*f
% 计算所有主成分的得分
df=xd*vec2
%% 通过累积贡献率交互式选择主成分的个数
num=input('请根据累积贡献率(contr值)输入主成分的个数：')
% 最小二乘法估计回归系数(最小二乘法的Matlab实现--左除\)
pca_hg=df(:,[1:num])\yd   % 主成分变量的回归系数，这里由于数据标准化，回归方程的常数项为0
% 标准化变量的回归方程系数
bz_hg=vec2(:,[1:num])*pca_hg
% 计算原始变量回归方程系数（第1分量是常数项）
hg=[mean(y0)-std(y0)*mean(x0)./std(x0)*bz_hg, std(y0)*bz_hg'./std(x0)]
% 显示主成分回归方程结果
fprintf('主成分回归方程：\n')
fprintf('y=%6.4f',hg(1))
for i=2:n
    if hg(i)>0
        fprintf('+%6.4f*x%d',hg(i),i-1)
    else
        fprintf('%6.4f*x%d',hg(i),i-1)
    end
end
fprintf('\n')

%% VI.计算两种回归分析的剩余标准差【均方根误差RMSE:越小越稳定】
ls_rmse=sqrt(sum((ls_hg(1)+x0*ls_hg(2:end)'-y0).^2)/(m-n)) % 最小二乘法回归(LSR)
rmse=sqrt(sum((hg(1)+x0*hg(2:end)'-y0).^2)/(m-num)) % 主成分回归(PCR)