开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 入门二叉树-一起来递归【下】 -> 正文阅读

[数据结构与算法]入门二叉树-一起来递归【下】

这次的题目相比较上次可能会难度上升，尤其是后面两题，反正不会就试着画图

1. 对称二叉树

本题目来源于leetcode 101. 对称二叉树

1.1 题目描述

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FwXkkTo8-1638356560463)(…/…/…/…/AppData/Roaming/Typora/typora-user-images/image-20211129092542774.png)]

1.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isSymmetric(struct TreeNode* root){

}

1.2 大致框架

1.2.1 思路与想法

注意按照题目的意思，只有镜像的才是对称的

如何判断一对称二叉树？

如果root为空，那么是对称。如果不为空的话，当他的左子树与右子树对称时，他才完全对称

2.那么怎么知道左子树与右子树对不对称呢？如果左树的左孩子与右树的右孩子对称，左树的右孩子与右树的左孩子对称，那么这个左树和右树就对称。

1.2.2 具体步骤

注意还是要先判空
要不断地比较左树的左孩子和右树的右孩子，以及左树的右孩子，和右树的左孩子
在此同时我们利用一个函数，接收一个left和一个right，进入递归
和之前判断相同的树一样，判断三种情况之后继续递归,分别是双空，单空和值不相等

1.3 整体实现

bool _isSymmetric(struct TreeNode* left, struct TreeNode* right) {
	if (left == NULL && right == NULL)
		return true;
	if (left == NULL || right == NULL)
	{
		return false;
	}
	if (left->val != right->val)
	{
		return false;
	}
	return _isSymmetric(left->left, right->right)
		&& _isSymmetric(left->right, right->left);
}
bool isSymmetric(struct TreeNode* root) {
	if (root == NULL)
	{
		return true;
	}
	return _isSymmetric(root->left, root->right);
}

2. 另一棵树的子树

本题目来源于leetcode 572. 另一棵树的子树

2.1 题目描述

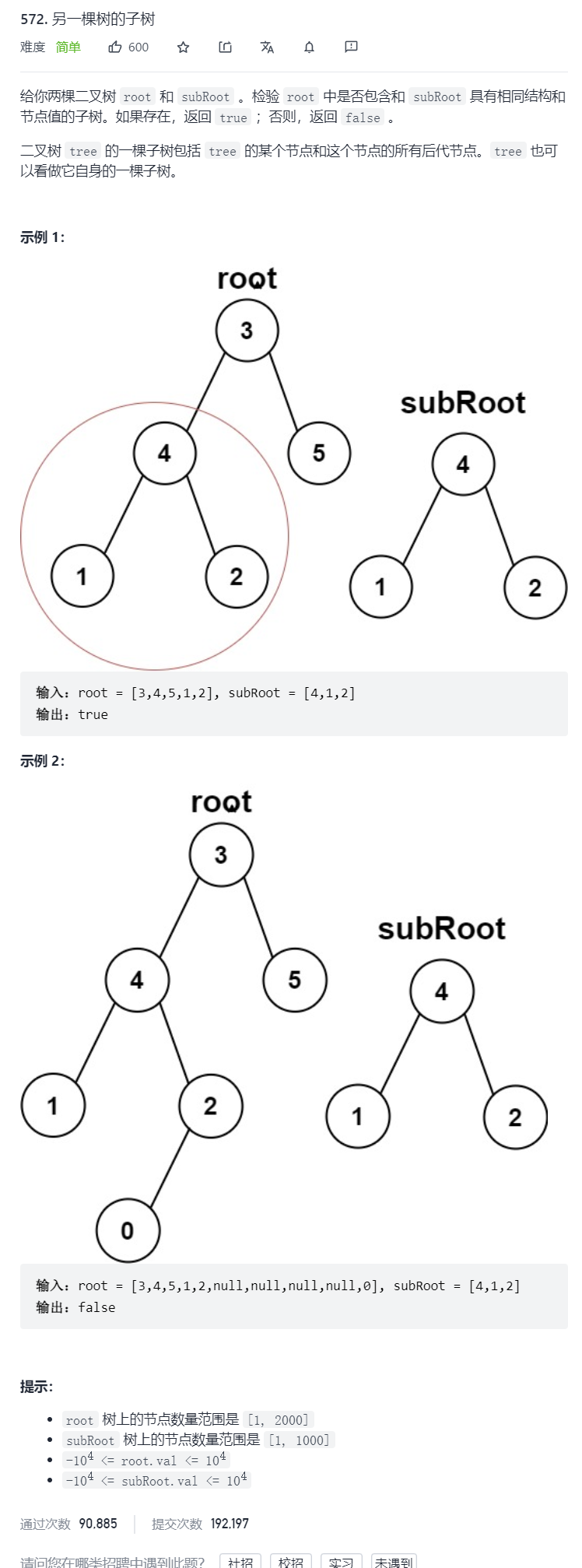
2.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){

}

2.2 大致框架

2.2.1 思路与想法

分析一下：t是s的子树的话，也就是说只要t和s的某一个子树相等，就满足了，也就是说t和s的所有子树都比较一遍，有相等就可以了

怎么才能算作每一个子树都比一遍？

相当于每一个子树都变成root根节点和t比一下

怎么遍历一遍?

层序遍历，或者前中后序都可以

2.2.2 具体步骤

本来就是相等的子树，那么返回true

那要实现一个判断相等的，借用之前的而一道题目

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
	if (p == NULL && q == NULL)
	{
		return true;
	}
	if (p == NULL || q == NULL)
	{
		return false;
	}
	if (p->val != q->val)
	{
		return false;
	}
	return
		isSameTree(p->left, q->left) &&
		isSameTree(p->right, q->right);
}

遍历每一个节点判断是不是和t一样

前序遍历就可以

先判断根，然后把左孩子和有孩子当作根，只要有一个对就return true

if (isSameTree(root, subRoot))
	{
		return true;
	}
	return isSubtree(root->left, subRoot) ||
		isSubtree(root->right, subRoot);//一棵子树相等就ok了

2.3 整体实现

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
	if (p == NULL && q == NULL)
	{
		return true;
	}
	if (p == NULL || q == NULL)
	{
		return false;
	}
	if (p->val != q->val)
	{
		return false;
	}
	return
		isSameTree(p->left, q->left) &&
		isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
	//遍历这一棵树的每一个节点
	if (root == NULL)
	{
		return false;
	}
	if (isSameTree(root, subRoot))
	{
		return true;
	}
	return isSubtree(root->left, subRoot) ||
		isSubtree(root->right, subRoot);//一棵子树相等就ok了
}

3. 平衡二叉树

本题目来源于leetcode110. 平衡二叉树

3.1 题目描述

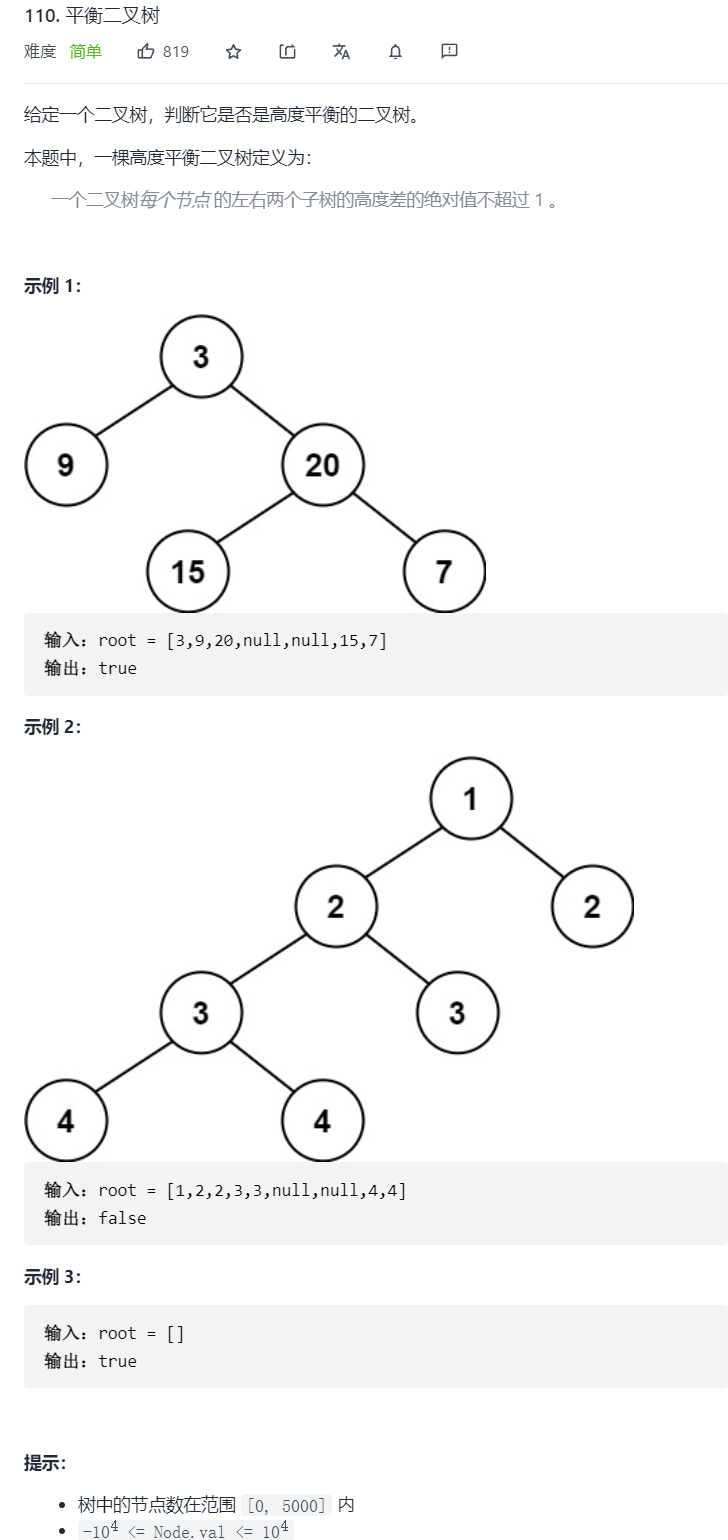
3.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isBalanced(struct TreeNode* root){

}

3.2 大致框架

3.2.1 思路与想法

先得有一个求高度的函数

方法一：

每个子树都要满足深度与另外一个子树是不能超过一的，所以要遍历没一个节点

时间复杂度：

递归了n次

每次递归（假设是满二叉树）就是
N N/2 N/2 N/4 N/4…
总的时间复杂度就是O（N²）

最好要优化一下，时间复杂度有一点高

方法二：

要求优化到O(N),我们发现前序实际上存在者重复运算。考虑一下使用后序能否实现一个简化。

先从后序来计算的话，会有什么好处，从深度最深的子树开始作为root，然后向上依次返回自己子树的最大高度，那只要遍历一遍就可以走完了

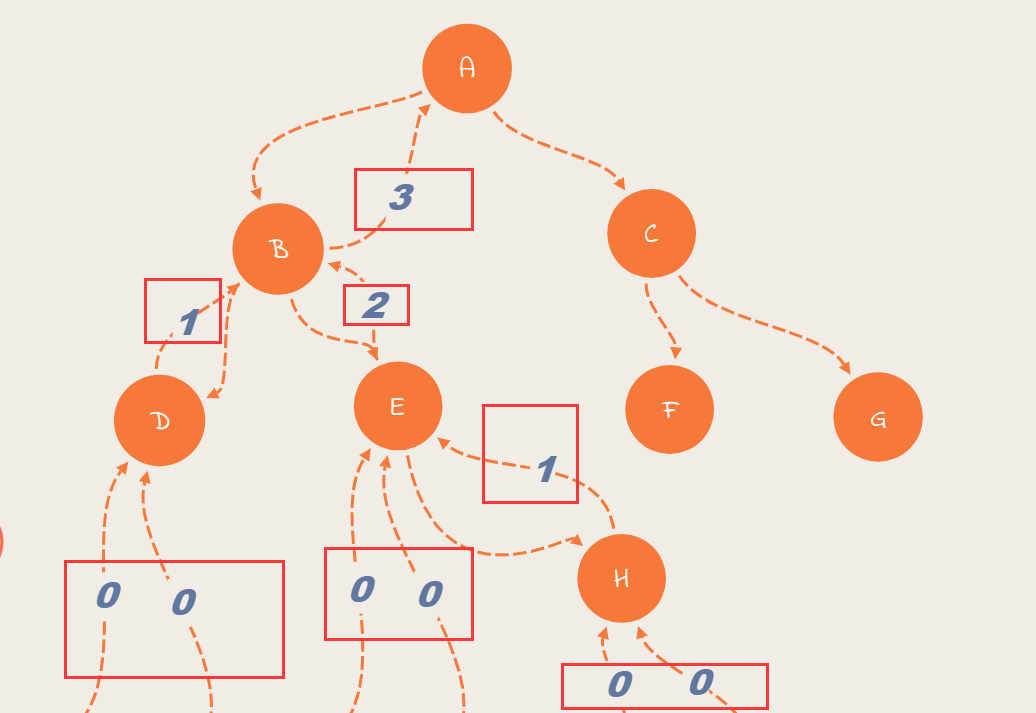
3.2.2 具体步骤

总归要先由一个求最大深度的函数、

int maxDepth(struct TreeNode* root) {
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = maxDepth(root->left);
	int rightDepth = maxDepth(root->right);
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

方法一：

前序遍历的方法遍历一遍子节点，比一下树的深度差是否是>2

方法二：

这里我们写一个_isBalanced函数，传值的时候注意h高度传地址，因为要实现修改，每次树最大高度都会变化

_isBalanced(root,&height)

找到最下面的节点使深度为0

if(root==NULL)
{
    *ph=0;
    return true;
}

然后对这样一个函数里面，凡是任意要有一个左数或者右树不满足，就false

注意：是调用_isBalanced而不是isBalanced

if(_isBalanced(root->left,&leftHeight)==false)
{
    return false;
}
int rightHeight=0;
if(_isBalanced(root->right,&rightHeight)==false)
{
    return false;
}

改变左右树的高度

*ph=fmax(leftHeight,rightHeight)+1;

最后这个函数判断是否平衡

return abs(leftHeight-rightHeight)<2;

3.3 整体实现

方法一

int maxDepth(struct TreeNode* root){
if(root==NULL)
{
    return 0;
}
int leftDepth=maxDepth(root->left);
int rightDepth=maxDepth(root->right);
return leftDepth>rightDepth?leftDepth+1:rightDepth+1;
}

bool isBalanced(struct TreeNode* root){
if(root==NULL)
{
    return true;
}
//前序，当前树就不是，不用判断后面的树了
int leftDepth=maxDepth(root->left);
int rightDepth=maxDepth(root->right);
return (abs(leftDepth-rightDepth)<2)
&&isBalanced(root->left)
&&isBalanced(root->right);
}

方法二

bool _isBalanced(struct TreeNode* root, int* ph) {
	if (root == NULL)
	{
		*ph = 0;
		return true;
	}
	//后序，先判断左子树再判断右子树
	int leftHeight = 0;
	if (_isBalanced(root->left, &leftHeight) == false)
	{
		return false;
	}
	int rightHeight = 0;
	if (_isBalanced(root->right, &rightHeight) == false)
	{
		return false;
	}
	//同时再把当前树的高度带给上一层
	*ph = fmax(leftHeight, rightHeight) + 1;
	return abs(leftHeight - rightHeight) < 2;
}

bool isBalanced(struct TreeNode* root) {
	int height = 0;
	return _isBalanced(root, &height);
}

4. 二叉树遍历

本题目来源于牛客网KY11二叉树遍历

4.1 题目描述

非接口形式，I/O型就全部自己写出来吧

4.2 大致框架

按照这道题给出的输入，化成二叉树应该是这样的形式

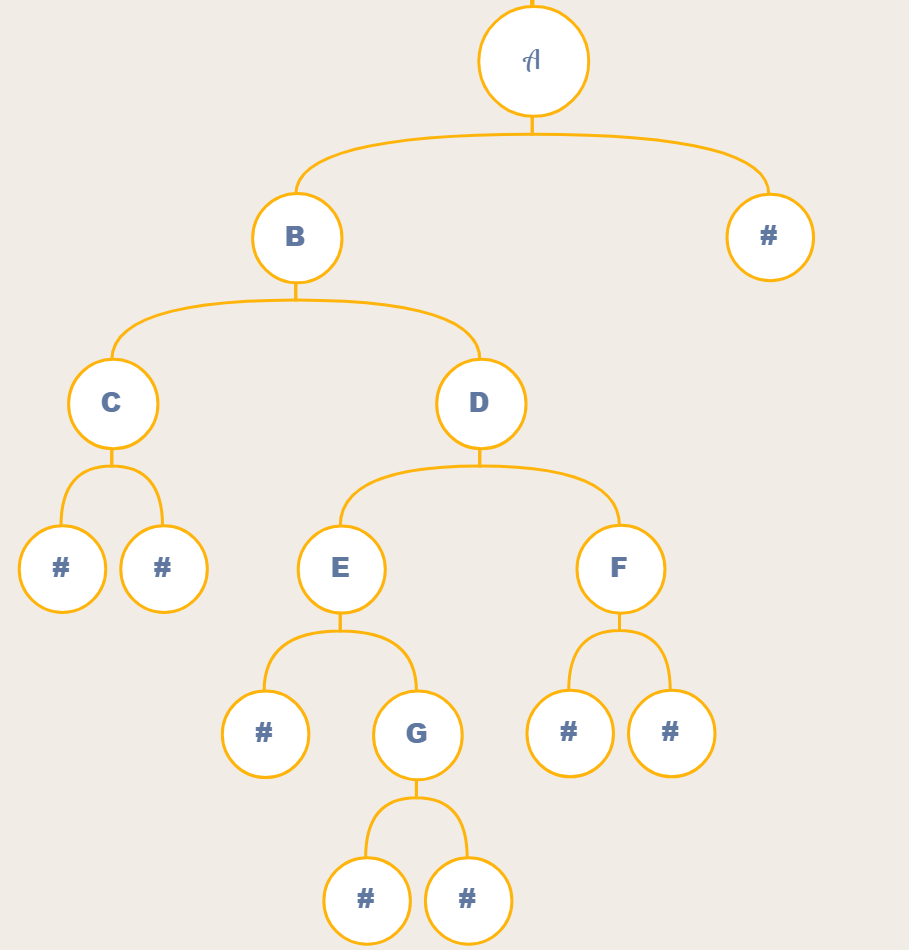
4.2.1 思路与想法

按照题目的意思，我们需要先通过前序来构建一个树，然后通过中序遍历方式输出这个树

4.2.2 具体步骤

先声明一个树

typedef struct TreeNode
{
    struct Treenode*left;
    struct Treenode*right;
    char val;
}TreeNode;

前序构建一个树

TreeNode * CreateTree(char* str,int *pi)
{
    if(str[*pi]=='#')
    {
        ++(*pi);
        return NULL;
    }
    
    //不是#，构建根
    TreeNode*root=(TreeNode*)malloc(sizeof(TreeNode));
    root->val=str[*pi];
    ++(*pi);
    //递归构建左子树
    root->left=CreateTree(str,pi);
    //递归构建右子树
    root->right=CreateTree(str,pi);
    return root;
}

中序输出

void InOrder(TreeNode*root)
{
    if(root==NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);
}

4.3 整体实现

#include<stdio.h>
#include<stdlib.h>
typedef struct TreeNode
{
    struct Treenode*left;
    struct Treenode*right;
    char val;
}TreeNode;

TreeNode * CreateTree(char* str,int *pi)
{
    if(str[*pi]=='#')
    {
        ++(*pi);
        return NULL;
    }
    
    //不是#，构建根
    TreeNode*root=(TreeNode*)malloc(sizeof(TreeNode));
    root->val=str[*pi];
    ++(*pi);
    //递归构建左子树
    root->left=CreateTree(str,pi);
    //递归构建右子树
    root->right=CreateTree(str,pi);
    return root;
}
void InOrder(TreeNode*root)
{
    if(root==NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);
}
int main()
{
    char str[100];
    scanf("%s",str);
    int i=0;
    TreeNode*root=CreateTree(str,&i);
    InOrder(root);
    printf("\n");
    return 0;
}

5. 二叉树的后序遍历

本题目来源于145. 二叉树的后序遍历

5.1 题目描述

5.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* postorderTraversal(struct TreeNode* root, int* returnSize){

}

5.2 大致框架

5.2.1 思路与想法

同前序遍历可以看上一篇博客

5.2.2 具体步骤

上一篇博客入门二叉树-一起来递归【上】

5.3 整体实现

  int TreeSize(struct TreeNode*root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }

void _postorder(struct TreeNode*root,int *arr,int *pi)
{
   if(root==NULL)
     return ;
   
     _postorder(root->left,arr,pi);
     _postorder(root->right,arr,pi);
       arr[(*pi)++]=root->val;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize){
*returnSize=TreeSize(root);
    int *arr=(int*)malloc(sizeof(int)*(*returnSize));
int i=0;
_postorder(root,arr,&i);
return arr;

}

6. 二叉树的中序遍历

本题目来自于 leetcode94. 二叉树的中序遍历

6.1.1 接口函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* inorderTraversal(struct TreeNode* root, int* returnSize){

}

6.2 大致框架

6.2.1 思路与想法

同前序遍历和后序遍历也可以看上一篇博客

6.2.2 具体步骤

上一篇博客入门二叉树-一起来递归【上】

6.3 整体实现

  int TreeSize(struct TreeNode*root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }
void _inorder(struct TreeNode*root,int *arr,int *pi)
{
    if(root==NULL)
    {
        return;
    }
    _inorder(root->left,arr,pi);
    arr[(*pi)++]=root->val;
    _inorder(root->right,arr,pi);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
 *returnSize=TreeSize(root);
 int *arr=(int*)malloc(sizeof(int)*(*returnSize));
 int i=0;
_inorder(root,arr,&i);
return arr;
}