[数据结构与算法]动规解 洛谷P1060开心的金明，SO EASY

题目：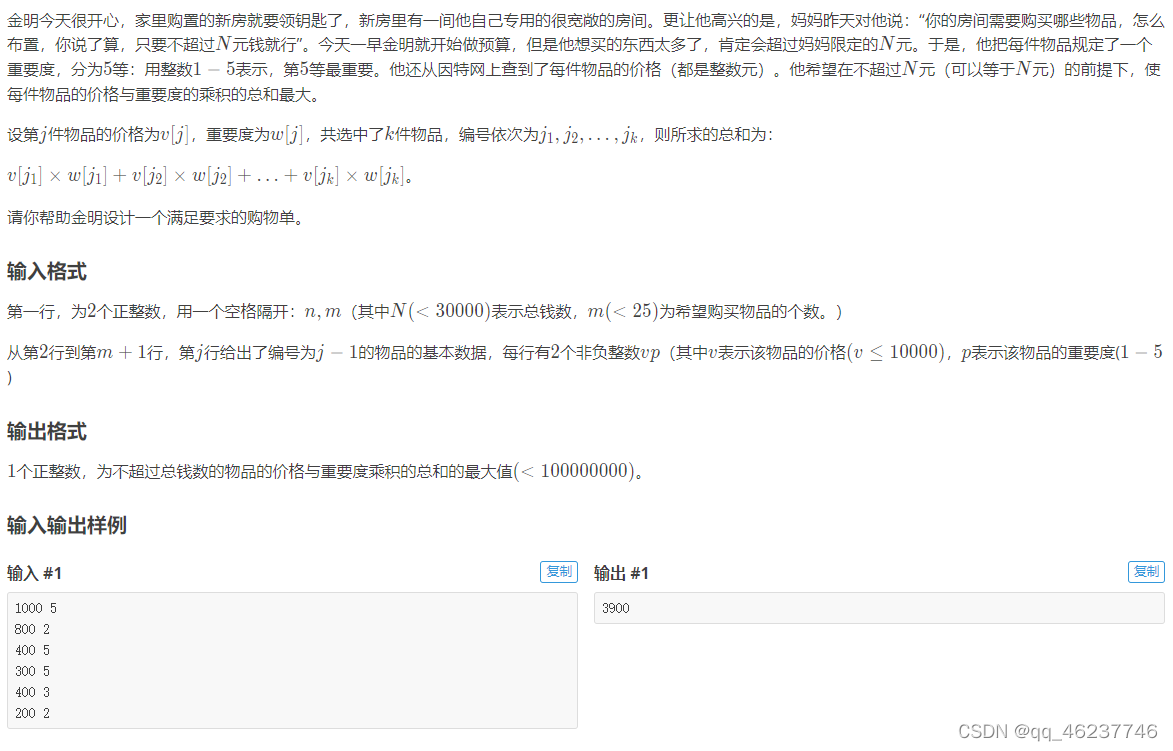

解体思路

这是一道0-1背包的一个变型

变量说明：
money：钱的数量；
num：商品数量
二维数组datas[i][j] ===> datas[i][0]： 商品价格 datas[i][1] 商品重要度
动态规划状态数组dp(i, j) 是最高总钱数为 j、有前 i 件物品可选时的 （价格*重要度）

状态分析
j<datas[i][0]时 dp[i,j]=dp[i-1][j]
j>datas[i][0]时 dp[i,j]=Math.max(dp[i-1][j],dp[i-1][j-datas[i-1][0]]+datas[i-1][1])

说明：
?dp(i – 1, j)：第i个物品不进行选择；

dp[i-1][j-datas[i-1][0]]+datas[i-1][1])：选择第i个物品，剩余金额为j-datas[i-1][0]， datas[i-1][1]第i件物品的价格 * 重要度的最大值；

dp[i-1][j-datas[i-1][0]]+datas[i-1][1])表示剩余金额为j-datas[i-1][0]，有前 i 件物品可选时的价格 * 重要度的最大值；

具体代码

public class Main {
	public static void main(String[] args) {
		Scanner in=new Scanner(System.in);
		int money=in.nextInt();//钱的数量
		int num=in.nextInt();//商品数量
		int[][] datas=new int[num][2];
		for (int i = 0; i < datas.length; i++) {
			for (int j = 0; j < 2; j++) {
				datas[i][j]=in.nextInt();
			}
		}
		in.close();
		//datas[i][0]价格     datas[i][1]重要度
		//dp(i, j) 是最高总钱数为 j、有前 i 件物品可选时的价格*重要度乘积
		/**
		 * j<datas[i][0]  dp[i,j]=dp[i-1][j]
		 * j>datas[i][0]  Math.max(dp[i-1][j],dp[i-1][j-datas[i-1][0]]+datas[i-1][1])
		 */
		int[][] dp=new int[num+1][money+1];
		for (int i = 1; i <= num; i++) {//前i个物品
			for (int j = 1; j <=money; j++) {//价格
				if(datas[i-1][0]>j) {
					dp[i][j]=dp[i-1][j];
				}else {
					//System.out.println(j);
					
					dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-datas[i-1][0]]+datas[i-1][1]*datas[i-1][0]);
				}
			}
		}
		System.out.println(dp[num][money]);
	}
}

代码优化

想一下，其实代码还可以优化，上面进行动态规划的数组dp(i, j)可以优化为一维数组，具体代码如下：

public class Main {
	
	public static void main(String[] args) {
		Scanner in=new Scanner(System.in);
		int money=in.nextInt();//钱的数量
		int num=in.nextInt();//商品数量
		int[][] datas=new int[num][2];
		for (int i = 0; i < datas.length; i++) {
			for (int j = 0; j < 2; j++) {
				datas[i][j]=in.nextInt();
			}
		}
		in.close();
		int[] dp=new int[money+1];
		for (int i = 1; i <= num; i++) {//前i个物品
			for (int j = money; j >=datas[i-1][0]; j--) {//价格
				//从右到左进行覆盖,当j < weights[i-1],证明第i件物品不能选
				dp[j]=Math.max(dp[j], dp[j-datas[i-1][0]]+datas[i-1][1]*datas[i-1][0]);
			}
		}
		System.out.println(dp[money]);
	}

}