[数据结构与算法]Java描述 LeetCode，55. Jump Game 跳跃游戏

大家好，我是河海哥，专注于后端，如果可以的话，想做一名code designer而不是普通的coder，一起见证河海哥的成长，您的评论与赞是我的最大动力，如有错误还请不吝赐教，万分感谢。一起支持原创吧！

1-1：题目

You are given an integer array nums. You are initially positioned at the array’s first index, and each element in the array represents your maximum jump length at that position.

Return true if you can reach the last index, or false otherwise.

Example 1:

Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.

Constraints:

1 <= nums.length <= 104
0 <= nums[i] <= 105

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/jump-game

1-2：动态规划解法1

1-2-1：idea-逆向思维

逆向思维，能不能走到n-1这个index上，可能从之前任何一个位置j走过来，我们站在j上，我们能走的范围是[ j: j+nums[j] ]这个范围，只要这个范围内出现了n-1这个位置，那么我就可以从j走到n-1这个index上。这个是逻辑是没有问题的。我们假设dp[n-1]是true，也就是最后一个位置。上面的话换言之，只要[ j: j+nums[j] ]这个范围出现了n-1的true，我就可以跳到n-1的位置上了。也就是成功到达最后一个位置。

那么，我们就可以考虑一般情况。i > j，要能够从j这个位置跳到i这个位置，也就是[ j: j+nums[j] ] 这个范围出现dp[i] = true。所以一步一步从后往前推，只要能推出dp[0] = true就可以喽。0到j，j到i，i再到n-1。差不多就是这个逻辑，中间可以经历很多个跳点。

1-2-2：dp几步

• 定义状态：dp[i] 代表能否跳到index为i的这个节点上。
• 状态转移方程：j=[i:i+nums[i]]范围内，dp[j]=true，dp[i]就是true。
• 初始化：dp[n-1] = ture。
• 遍历顺序：从后向前。

1-2-3：代码

public static boolean canJump2(int[] nums) {
    int n = nums.length;

    boolean[] dp = new boolean[n];
    dp[n - 1] = true;

    for (int i = n - 2; i >= 0; i--) {
        for (int j = i + 1; j <= i + nums[i]; j++) {
            if (dp[j] == true) {
                dp[i] = true;
                break;
            } else {
                dp[i] = false;
            }
        }
    }

    System.out.println(Arrays.toString(dp));
    return dp[0];
}

1-3：动态规划解法2

1-3-1：idea

上面的是逆向思维，如果我们正向思维，我们直接从一般情况考虑，假设j<i，怎么判断能不能从j的位置跳到i上面呢？首先，dp[j]本身就得是true，都到不了j上，更别说到i了，对不对，剩下的就是怎么才能保证能从i上跳到j上呢？nums[j]代表j最多能跳的距离，只要i和j的距离小于nums[j]，就可以知道一定可以从j跳到i上了。再次泛化，怎么才能到index为i的位置上呢？存在一个j，当i>j时，i-j<=nums[j]，即可。

1-3-2：代码

public static boolean canJump(int[] nums) {
    int n = nums.length;
    boolean result[] = new boolean[n];
    // 初始条件
    result[0] = true;
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            // 能不能到j上，并且能不能从j的位置跳到i的位置
            if (result[j] == true && (i - j) <= nums[j]) {
                result[i] = true;
                break;
            } else {
                result[i] = false;
            }
        }
    }
    return result[n - 1];
}

1-4：贪心解法1

1-4-1：idea

这是我自己的思路我也不知道算不算的上贪心，我的思路是，对于一个index=i，我把它所有能到的地方都设置为true，对于另外一个index=j，只要j在i的步数内，并且nums[j] 不是0，就可以继续往前走。那么什么情况，就无法继续前进呢？首先nums[j] == 0，并且前面的路都不可能通过其他index过去比如[1, 0, 0] [T, T , F]，但是[1,2,0] [T, T ,T]就可以通过2跳过去，也就是说，我只能通过j这个位置进行下一步了，但是刚好j的最大步数只能是0，就不可能再到达终点了。

1-4-2：代码

public static boolean canJump(int[] nums) {
    int n = nums.length;
    boolean[] results = new boolean[n];
    if (n == 1) {
        return true;
    }

    if (nums[0] == 0) {
        return false;
    }

    results[0] = true;
    for (int i = 0; i < n; i++) {
        if (nums[i] == 0 && i + 1 < n && results[i + 1] == false) {
            return false;
        }

        for (int j = 1; j <= nums[i]; j++) {
            if (i + j <= n - 1) {
                results[i + j] = true;
            }
        }
    }
    System.out.println(Arrays.toString(results));
    return results[n - 1];
}

1-4-2：自己的优化想法

可以看出来，这里有一部分是重复赋值为true的，当他们的步数有重合部分的时候，于是我就想着 跳过这部分重合的地方。于是我写了下面的代码，调试了一会。

public static boolean canJump2(int[] nums) {
    int n = nums.length;
    if (n == 1) {
        return true;
    }
    boolean[] results = new boolean[n];
    int i = 0;
    while (i < n - 1) {
        // 无路可走
        if (nums[i] == 0) {
            return false;
        }

        //下一步到开始
        int j = i + 1;
        while (j <= i + nums[i] && j < n) {
            results[j] = true;
            j++;
        }

        // 能走到到最后一步
        i = j - 1;
        if (i < n - 1 && results[i] == false) {
            return false;
        }
    }
    return results[n - 1];
}

测试结果：

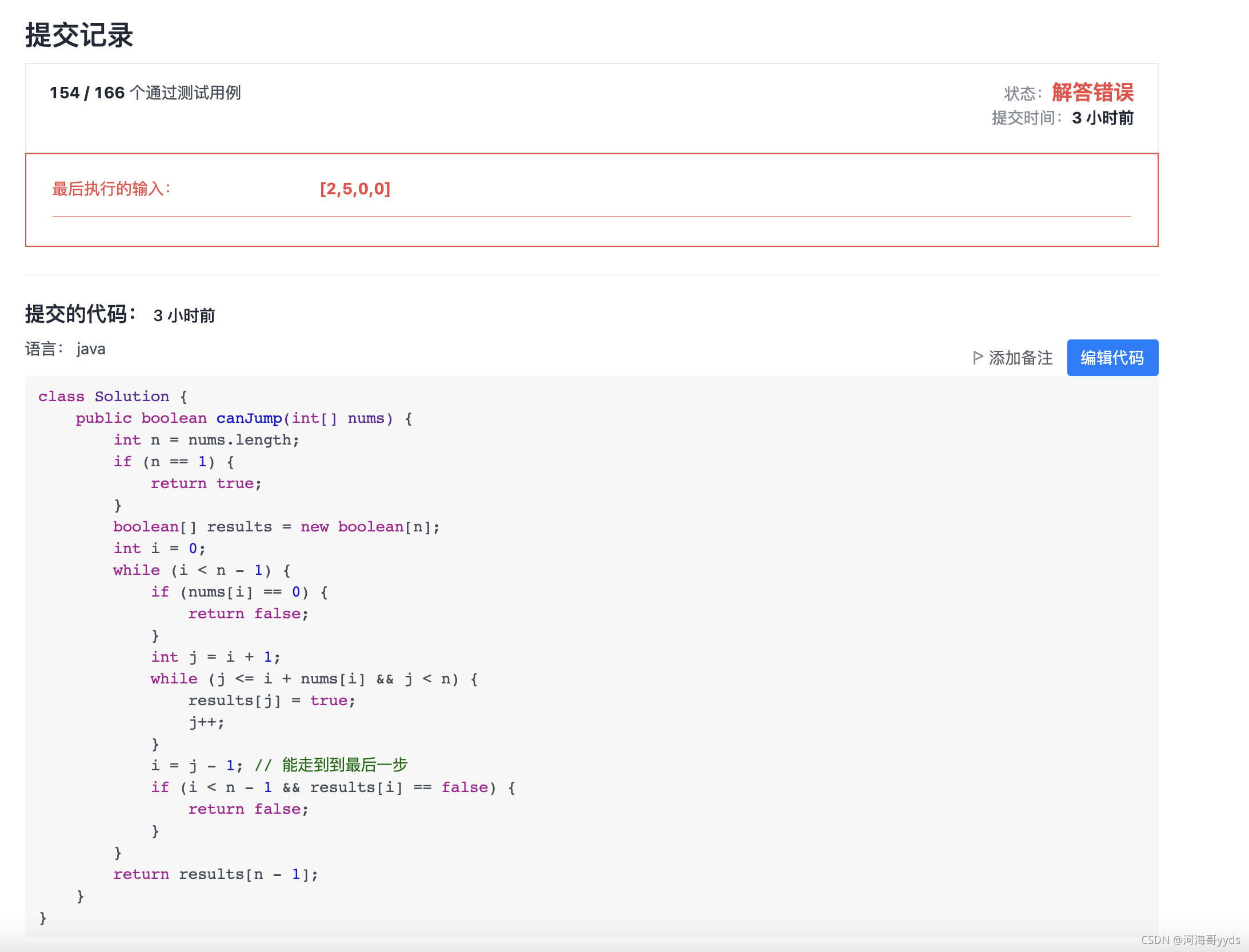
可以发现，跳过的代价就是忽略了中间的大佬，比如这里的5，明明可以通过它到达最后一个的，但是由于我跳过了，所以5被忽略了。所以这里的代码有问题，虽然通过了154/166但是fail。

1-5：贪心解法2

1-5-1：idea

也就是答案，最牛批的解法，维护一个能跳到的最大的范围，只要这个最大的范围在遍历的时候把最后一个位置包含在内，就说明可以跳到那边，不需要考虑所有的位置，也就是说不用维护能不能到达的所有的结点的数组。

1-5-2：代码

public static boolean canJump3(int[] nums) {
    int n = nums.length;
    int rightmost = 0; // 能到达的最远index
    for (int i = 0; i < n; i++) {
        if (i <= rightmost) { // 只要还在这个范围内，就可以继续跳。
            // 可能出现[...5,0,0]这种情况，这次的不如上次的远
            rightmost = Math.max(rightmost, i + nums[i]);
            if (rightmost >= n - 1) {
                return true;
            }
        }
    }
    return false;
}

这个代码太妙了哇！每一个代码都体现了，智慧！

1-6：总结

dp代码是我自己写的，还不错也算ac了。答案的贪心算法，想不到，算是又涨了见识。最近期末了，只能多抽点时间来耍力扣了。有时间就整，不能成为算法fw啊！加油！hhg。😊