描述
给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1?和?o2,请找到 o1?和?o2?的最近公共祖先节点。
数据范围:1 \le n \le 10001≤n≤1000,树上每个节点的val满足?0<val \le 1000<val≤100
要求:空间复杂度?O(1)O(1),时间复杂度?O(n)O(n)
注:本题保证二叉树中每个节点的val值均不相同。
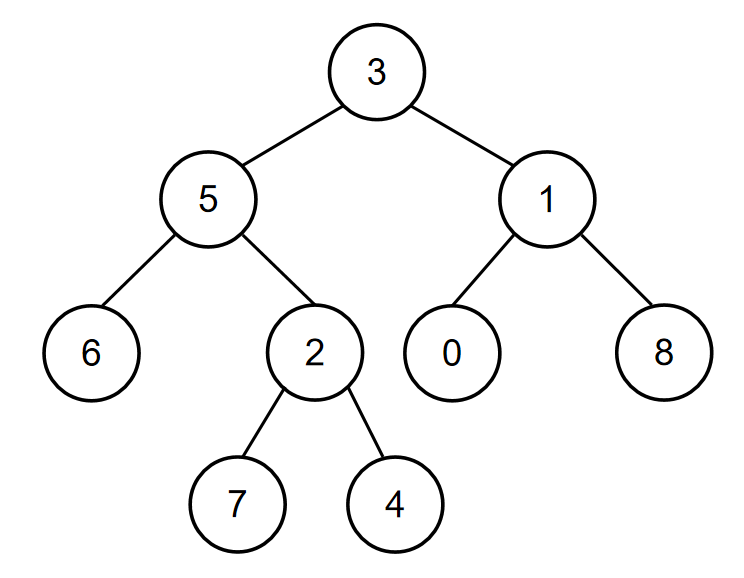
如当输入[3,5,1,6,2,0,8,#,#,7,4],5,1时,二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示:
?
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3,所以对应的输出为3。
示例1
输入:
[3,5,1,6,2,0,8,#,#,7,4],5,1
返回值:3
一开始拿到题的时候我会想依次往上寻找,当两个节点找到同一个值了,它便是最近公共祖先,但是有个问题,先得遍历找到节点,并且把遍历经过的节点存储起来,当离节点远的时候,很难判断这个节点是否应该存储起来。
解题思路参考了二叉搜索树的最近公共祖先,因为二叉搜索树一定是左<根<右,从根节点遍历,有三种情况,一种情况是当根节点大于两个给出的节点,则这两个节点是在根节点的左子树,把左结点作为根节点继续往下查找,第二种情况是当根节点小于两个给出的节点,则这两个节点是在根节点的右子树,把右结点作为根节点继续往下查找,第三种是根节点处于中间,那么此时根节点就是最近公共祖先
同样的,本题也从根节点出发往下判断,加入当前节点为空,或者当前节点值等于其中某个节点值,那么当前节点就是最近公共祖先,如果都不满足,那么分别从左右继续往下遍历,当前节点有可能是最近公共祖先,也可能不是。如果是的话,往左能找到一个给定的节点值,往右也能找到一个给定的节点值,如果不是的话,两个节点要么同在左子树,要么同在右子树,返回对左右子树递归得到的非空的节点值
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
class Solution {
public:
/**
*
* @param root TreeNode类
* @param o1 int整型
* @param o2 int整型
* @return int整型
*/
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
// write code here
if(root==nullptr)
{
return 0;
}
if(root->val == o1 || root->val == o2)
{
return root->val;
}
int left = lowestCommonAncestor(root->left,o1,o2);
int right = lowestCommonAncestor(root->right,o1,o2);
if(left && right)
{
return root->val;
}
return left?left:right;
}
};