关于一些简单算法的思想
前言前几天做了HDU的一道水题,感觉自己的想法挺有趣的,仔细查找后发现这种想法原来叫做“尺取思想”。
一、尺取思想是什么?尺取思想:就是面对一组数据时,如同尺子一样,去一段一段的截取你所需要的序列。
具体是如何呢,例题如下。
二、例题
1.题目概括(HDU-5776)
2.思维图
该题目核心考察的是:当给你一大段连续序列时,你是否能 从中找到一段连续子序列,使得该一段连续子序列的和等于M。例如:
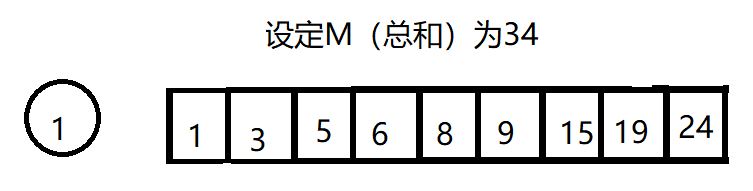
?此时总和 M 为34,我们不妨从第一项 “1” 开始当作连续序列的开头。
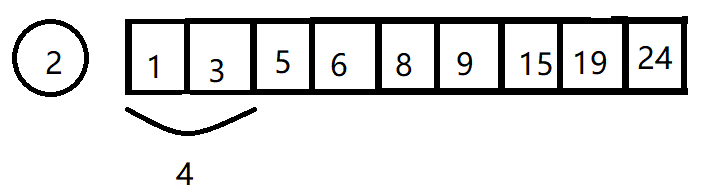
我们往后增加子序列元素,此时子序列为{1、3},总和为4,远远不到34,我们继续。
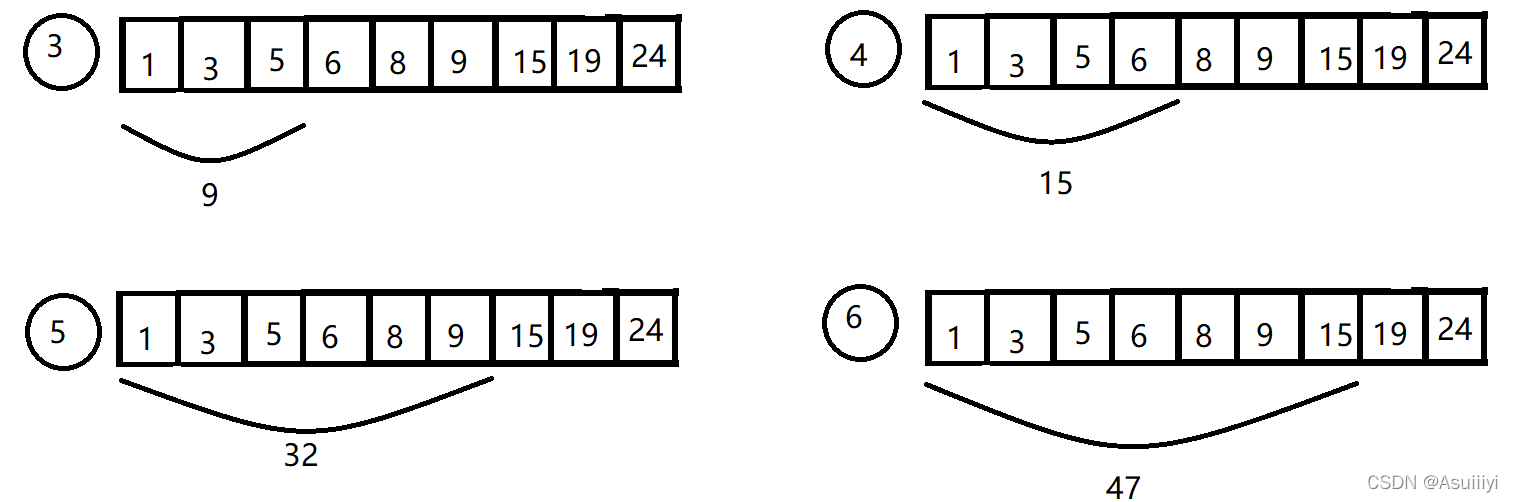
?直到第五步,所选连续序列中已经有了“1”,“3”,“5”,“6”,“8”,“9”,总和为32,很接近M的大小,我们继续。
判断点:到第六步,序列中增加了一个“15”,此时总和达到了47,明显大于34,已经超出M的大小,说明再往后添加是不可行的,这也说明了,我们用 “?1 ”当作序列开始不可行,我们决定把“1”减掉。
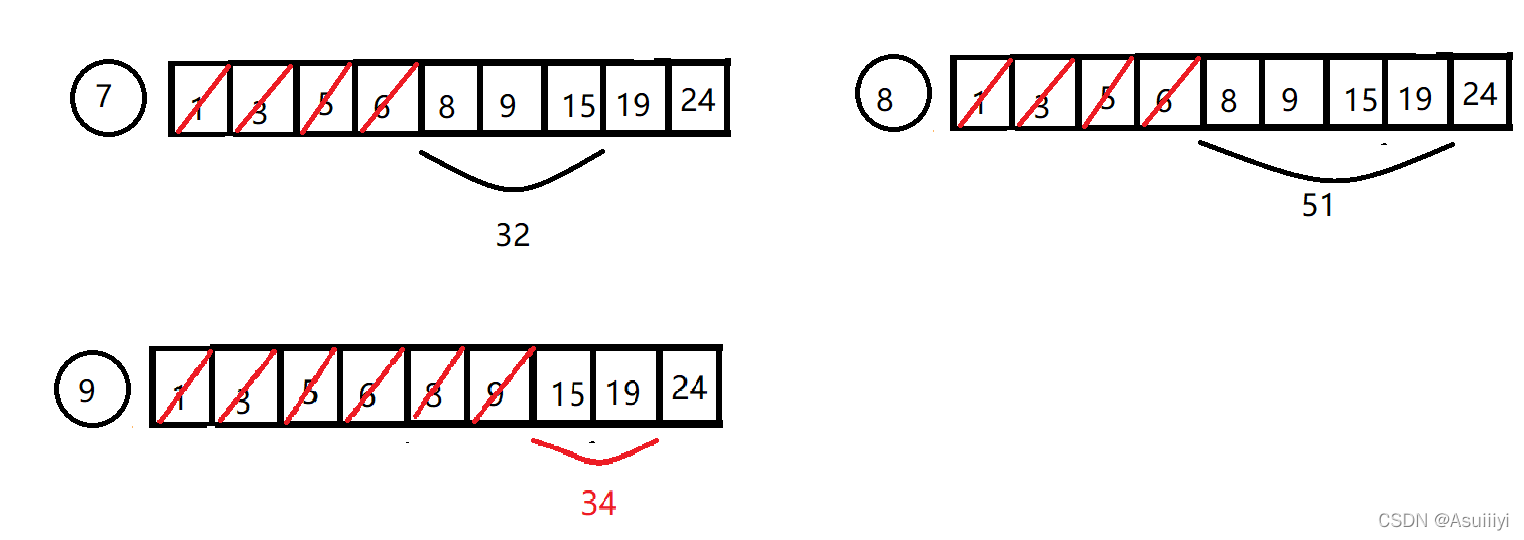
然后我们发现采取减开头的方法,直到第七步,“6”减去,让“8”当作子序列的开头时,此时子序列总和等于32,小于M。我们可以意识到子序列需要往后添加元素,才有可能使得子序列总和等于M,因此有了第八步。
经过我们一番折腾,终于在第九步,发现有一个子序列的总和与M的大小相匹配,该子序列为{15、19}。
总结不难发现规律,当子序列大于M总和时,我们需要将 子序列 前端元素进行删减,当子序列小于M总和,我们需要 往后增加 子序列 元素,一直进行如此操作,直到子序列总和与M匹配,或者增加了总序列的最后一位元素,也没有与M匹配,判断为“没有子序列使得总和等于M”。? ? ?而这样的操作,就如同尺子般,一段一段去截取序列,然后进行判断,这就是所谓的“尺取思想”。
该题的AC代码实现:(当时做的时候想到这么做就写上去了,AC以后也没进行进一步的优化了,如果各位前来阅读的佬们 有什么特别好的想法,也可以私信我(让我白嫖代码)。)
#include<stdio.h>
#include<string.h>
int arr[100009] = { 0 };
int main()
{
int T,n, M, i, j, k, l,flag;
int add=1, dec=1,sum=0;
scanf("%d", &T); //表示有T组数据
for (i = 1; i <= T; i++)
{
memset(arr, 0, sizeof(arr));//每次输入一组数据前,将上组存入 数组 中的 数据 初始化
scanf("%d %d", &n, &M);//M是总和
for (j = 1; j <= n; j++)
{
scanf("%d", &arr[j]);//将总序列存入 数组 arr
}
flag = 0;sum = 0;add = 1;dec = 1;//计算部分
while (sum != M)
{
//判断跳出
if (add == n+1 && sum != M)
{
flag = 1;//如果总序列最后一位元素进去也没有与M匹配的子序列,将flag标记为 1 ,然后跳出循环判断
break;
}
for (int i = add; i<=n && sum < M; i++)//循环在子序列总和没有 大于M 之前不会停止,同时add的标记也不会停止
{
sum += arr[i];
add = i; //add作用是:标记当前 需要往后增加的 元素 在数组中的位置
if (sum == M)
break;
}
add++;
for (int i = dec; i<=n && sum > M; i++)//循环在子序列总和 没有小于M 之前不会停止,同时dec的标记也不会停止
{
sum -= arr[i];
dec = i; //dec作用是:标记当前 需要往前删减的 元素 在数组中的位置
if (sum == M)
break;
}
dec++;
}
if (flag == 1)//flag为 1 即没有子序列的总和与 M 匹配
printf("NO\n");
if (flag == 0)
printf("YES\n");
}
return 0;
}