[数据结构与算法]二叉树前中后序遍历及其本质

二叉树前中后序递归的本质

二叉树递归实现前中后序遍历非常的简单，只需要调整处理语句出现的位置即可。

void order(TreeNode* root)
{
	if (!root)	
		return;

	//前序
	order(root->left);
	//中序
	order(root->right);
	//后序
}

二叉树每个节点都会被经过三次，我们使其每个位置都打印节点。

void order(TreeNode* root)
{
	if (!root)
		return;

	cout << root->val << " ";
	order(root->left);
	cout << root->val << " ";
	order(root->right);
	cout << root->val << " ";
}

如果只取第一次出现的节点，那就是前序遍历，只取第二次出现的节点那就是中序遍历，只取第三次出现的节点就是后序遍历。这种遍历序列可以称为递归序。

非递归实现前中后序

前序遍历

前序遍历非递归比较好理解，需要利用到一个栈来模拟递归过程。

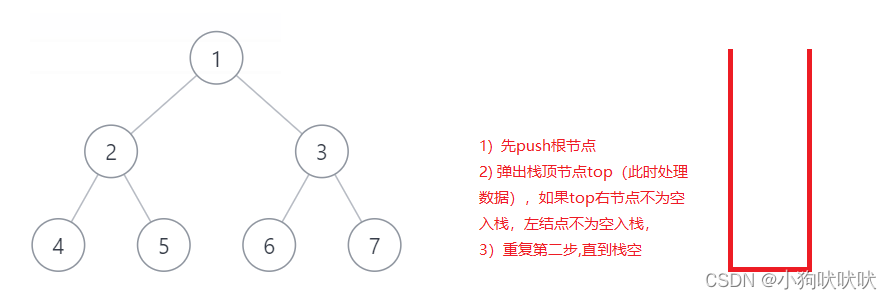
代码示例：

void prevOrderNonR(TreeNode* root)
{
	if (!root)	return;

	stack<TreeNode*> st;
	st.push(root);
	while (!st.empty())
	{
		TreeNode* cur = st.top();
		st.pop();
		cout << cur->_val << " ";
		
		if (cur->_right)
			st.push(cur->_right);
		if (cur->_left)
			st.push(cur->_left);
	}

}

后续遍历：

上面使用栈实现了二叉树的前序遍历，在此基础上稍作修改就可以实现后续遍历。
众所周知，二叉树的前序遍历顺序为 左子树 右子树 根。

我们改变前序遍历的压入节点的顺序，原先为先push右子树，再push左子树。现在改变其顺序，先压左，在压右。
此时前序遍历的顺序变为 右子树 左子树 根。

后序遍历的顺序为 左子树 右子树 根，有没有发现，后序遍历序列的顺序就是上述变形序列的逆序。

代码示例:

 vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(!root)   return ret;

        stack<TreeNode*> helper;
        stack<TreeNode*> post;
        helper.push(root);

        while(!helper.empty())
        {
            TreeNode* node = helper.top();
            helper.pop();
            post.push(node); // 并不直接处理，存入一个栈中

            if(node->left)
                helper.push(node->left);  //改变节点入栈顺序，先压左 
            if(node->right)
                helper.push(node->right);//再压右
        }
		//此时这个栈的弹出序列就为后序遍历序列
        while(!post.empty())
        {
            ret.push_back(post.top()->val);
            post.pop();
        }

        return ret;
    }

中序遍历：

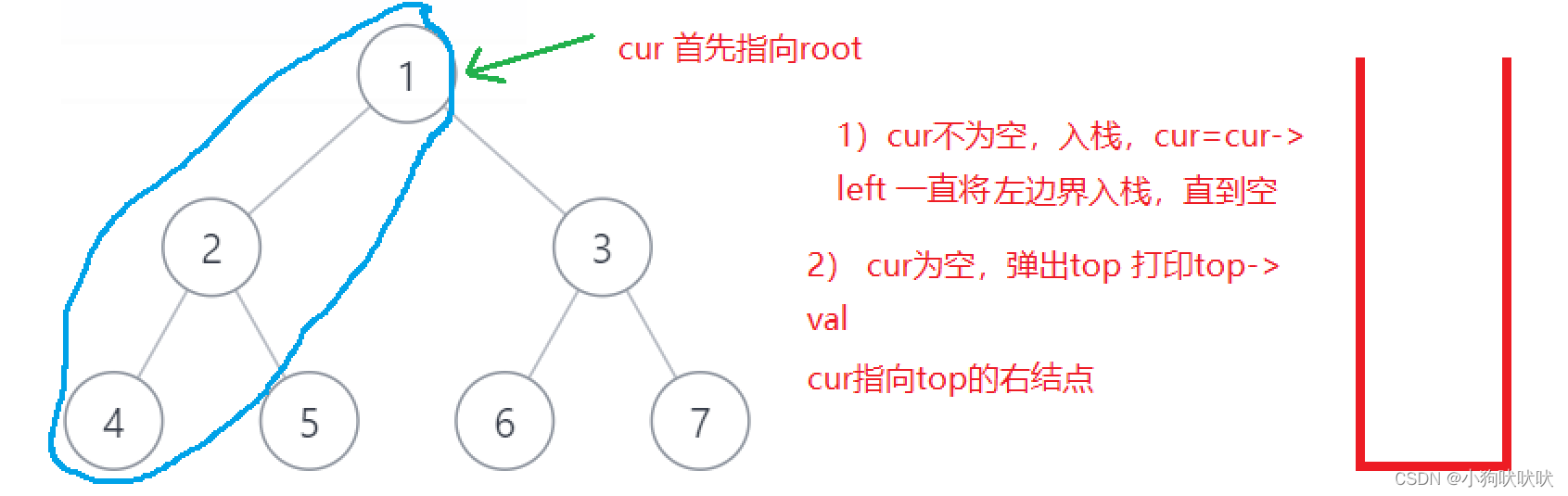
代码示例：

void inOrderNonR(TreeNode* root)
{
	if (!root)	return;

	stack<TreeNode*> st;
	TreeNode* cur = root;
	while (cur || !st.empty())
	{
		if (cur != nullptr)
		{
			st.push(cur);
			cur = cur->_left;
		}
		else
		{
			cur = st.top();
			st.pop();
			cout << cur->_val << ' ';
			cur = cur->_right;
		}
	}
}