B站学习传送门–>尚硅谷Java数据结构与java算法(Java数据结构与算法)
1.情景引入
一个简单的0-1背包问题;规定背包的最大容量是4公斤;并且放入背包的物品不能重复,怎么样让背包的物品价值量最大化?
| 物品 | 重量 | 价值 |
|---|---|---|
| 电脑 | 1 | 6000 |
| 电子琴 | 4 | 8000 |
| 游戏机 | 3 | 3000 |
动态规划算法的思想也是将复杂问题规划分解为小问题,但是和分治算法不同的地方是,
动态规划算法分解得到的子问题有递进关系;子问题的最优解会成为最终的解;
可以这么看;分解得到的子问题的求解是建立在上一个阶段子问题的求解基础上;这些子问题不是相互独立的;
2.背包问题分析
接着回到之前的背包问题;
首先,背包问题就是给定一个固定容量的背包,多个具有不同价值的物品;如何让背包的价值最大?
背包问题可分为01背包问题和完全背包问题;
01背包:规定放入背包的每种物品不能重复;
完全背包:放入背包的每种物品数量可不限数量;
实际上无限背包问题可转换为01背包问题
回到这个问题
对于这个问题,直接写公式的话不利于理解;
可以先进行填表式的分解;
先假设将背包的容量分为0,1,2,3,4;逐个添加物品;
(1)只有电脑一种物品时,背包容量再怎么递增,价值也只能是6000;
(2)物品为电脑和电子琴时,介于电子琴的重量为4,所以在背包容量为4时,会比较上一步的背包容量为4时的最优解;这时发现电子琴的价值大,则将电子琴放入背包;
(3)物品为电脑,电子琴和游戏机时;在背包容量为3时,会比较上一步子问题背包容量为3的最优解,这时比较发现将重量为1的电脑放入可实现价值最大,当背包容量为4时,同样会进行比较上一步背包容量为4时的最优解;
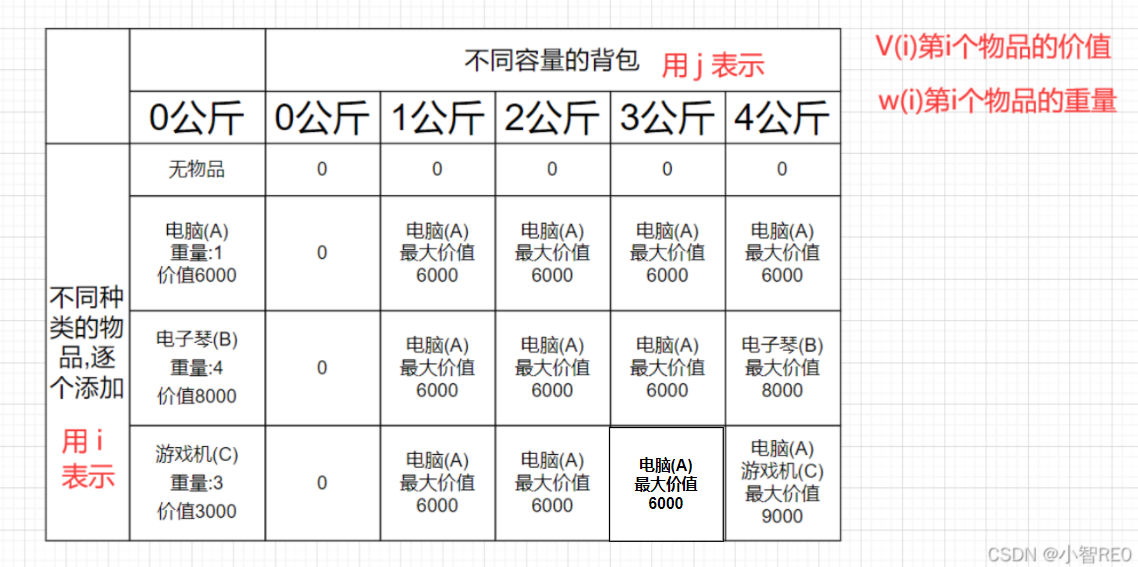
那么再进行转换,让 i表示 增加的第几个物品; j表示哪个容量的背包(这里背包的容量是递增的)
v(i) 表示当前 第 i 个物品的价值 ;
w(i)表示当前 第 i 个物品的重量 ;
那么v(i)(j) 表示在容量为 j的背包中, 用i种物品所能存放的最大价值;
分为三种情况:
(1):背包容量为0的情况;以及没有物品的情况
v(i)(0) = v(0)(i) = 0
(2)在添加第i个物品时,要是当前物品的重量已经大于背包的容量了;那么直接用上一步骤的物品的最大价值填充;在表中看得话就是同列上一个格子的数据;
当 w(i) > j 时;
当前的最大价值 v(i)(j) = v(i-1)(j)
(3)在添加第i个物品时,若当前物品的重量小于或者等于背包的容量,就得同上一步的进行比较了;
当 w(i) <= j 时;
当前的最大价值 v(i)(j) = Math.max( v(i-1)(j) , v(i-1)(j-w(i)) )
这里说明一下:
v(i-1)(j) 上一步的最优解;
-----------------------------------
v(i) : 当前的物品价值 ;
-----------------------------------
v(i-1)(j-w(i)) : 分布说明: j:当前背包的最大容量 ; j-w(i):背包放入当前物品后的剩余容量; (i-1)上一步的物品
那么v(i-1)(j-w(i)) :就是在背包放入当前物品后剩余空间的价值;
----------------------------------
当前的最大价值 v(i)(j) = Math.max( v(i-1)(j) , v(i-1)(j-w(i)) )
会对这两个价值进行比较;
3.背包问题的解决
public class KnapsackProblem {
//测试
public static void main(String[] args) {
Knapsack();
}
public static void Knapsack() {
//放置商品单个价值的数组;
int[] shopVal = {6000, 8000, 3000};
//放置单个商品重量的数组;
int[] weight = {1, 4, 3};
//背包的最大容量定义为4;
int m = 4;
//商品的数量;
int n = shopVal.length;
//商品与背包关系的数组;
int[][] dp = new int[n + 1][m + 1];
//首先对第一行第一列进行初始化;
for (int i = 0; i < dp.length; i++) {
dp[i][0] =0;
}
for (int i = 1; i < dp[0].length; i++) {
dp[0][i]=0;
}
//进行放置操作; 注意会从第一行之后,第一列之后的区域开始;
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j <dp[0].length ; j++) {
//若当前商品的重量超过背包容量的最大值;继承上一步的最优值;
if(weight[i-1]>j){
dp[i][j]=dp[i-1][j];
}
else {
//当前商品的重量不超过背包容量的最大值;需要和之前的进行比较;
dp[i][j]=Math.max(dp[i-1][j] , shopVal[i-1]+dp[i-1][j-weight[i-1]]);
}
}
}
//打印信息;
for (int[] ints : dp) {
for (int j = 0; j < dp[0].length; j++) {
System.out.print(ints[j] + "\t\t");
}
System.out.println();
}
}
}
测试输出;
这样只是将分析的表做出来了,并没有达到最终的要求,无法看出是把什么物品放入了背包
0 0 0 0 0
0 6000 6000 6000 6000
0 6000 6000 6000 8000
0 6000 6000 6000 9000
优化改进
public class KnapsackProblem {
//测试
public static void main(String[] args) {
Knapsack2();
}
public static void Knapsack2() {
//放置商品单个价值的数组;
int[] shopVal = {6000, 8000, 3000};
//放置单个商品重量的数组;
int[] weight = {1, 4, 3};
//背包的最大容量定义为4;
int m = 4;
//商品的数量;
int n = shopVal.length;
//商品与背包关系的数组;
int[][] dp = new int[n + 1][m + 1];
//走过的路径进行标记;
int[][] path = new int[n+1][m+1];
//物品名称数组;
String[] things = {"A电脑","B电子琴","C游戏机"};
//首先对第一行第一列进行初始化;
for (int i = 0; i < dp.length; i++) {
dp[i][0] = 0;
}
for (int i = 1; i < dp[0].length; i++) {
dp[0][i] = 0;
}
//进行放置操作; 注意会从第一行之后,第一列之后的区域开始;
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
//若当前商品的重量超过背包容量的最大值;继承上一步的最优值;
if (weight[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
//当前商品的重量不超过背包容量的最大值;需要和之前的进行比较;
if (dp[i - 1][j] > shopVal[i - 1] + dp[i - 1][j - weight[i - 1]]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = shopVal[i - 1] + dp[i - 1][j - weight[i - 1]];
//标记;
path[i][j]=1;
}
}
}
}
//打印信息;
System.out.println("------分析背包问题-----");
for (int[] ints : dp) {
for (int j = 0; j < dp[0].length; j++) {
System.out.print(ints[j] + "\t\t");
}
System.out.println();
}
System.out.println("-----寻找存放的最优解-------");
//只需找最后一次的;
int i1 = dp.length-1;
int i2 = dp[0].length-1;
while (i1>0 && i2>0){
if(path[i1][i2]==1){
System.out.printf("第%d个物品"+things[i1-1]+"放入背包\n",i1);
i2 = weight[i1-1];
}
i1--;
}
}
}
测试输出
------分析背包问题-----
0 0 0 0 0
0 6000 6000 6000 6000
0 6000 6000 6000 8000
0 6000 6000 6000 9000
-----寻找存放的最优解-------
第3个物品C游戏机放入背包
第1个物品A电脑放入背包