[数据结构与算法]【Java数据结构】二叉树leetcode经典题目详解，一学就会，一看就懂

目录

前言

①二叉树前序遍历

②二叉树中序遍历

③二叉树后序遍历

④检查两棵树是否相同

⑤二茶树的最大深度

⑥另一颗树的子树

⑦判断一颗树是否为一颗平衡二叉树

⑧对称二叉树

⑨二叉树镜像

前言

二叉树是笔试面试的重点，如果你对基础不够了解，建议先阅读我的这篇博客回归总结一下

【Java数据结构】挑战全网最细节图解二叉树前、中、后序遍历

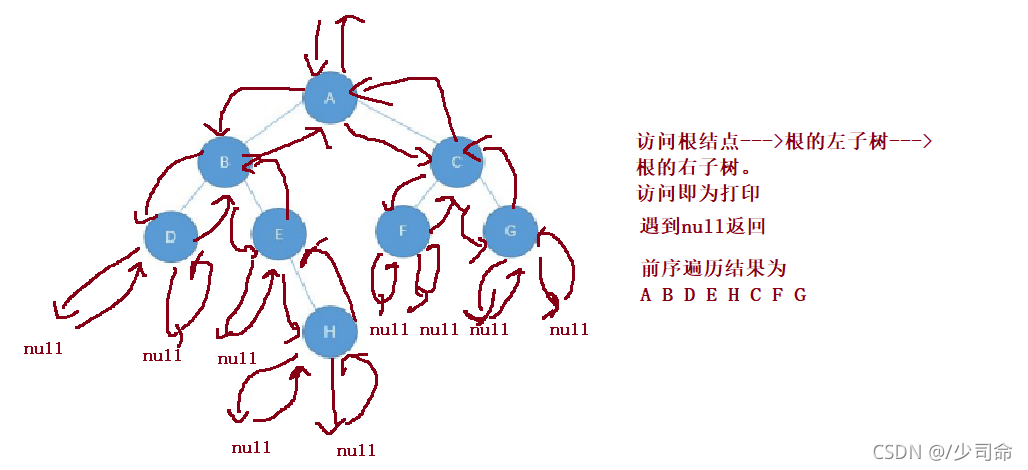
①二叉树前序遍历

?

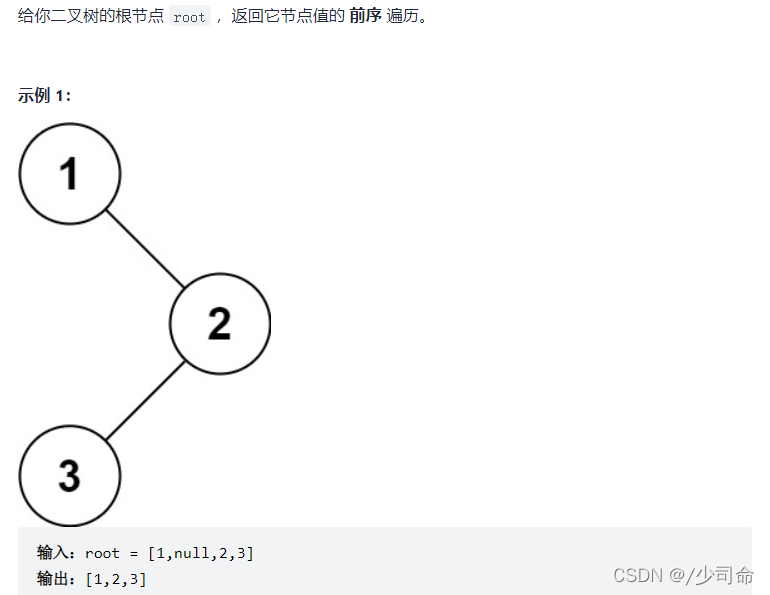
  void preOrderTraversal(TreeNode root){
        if(root == null) {
            return;
        }
        System.out.print(root.val+" ");
        preOrderTraversal(root.left);
        preOrderTraversal(root.right);
    }

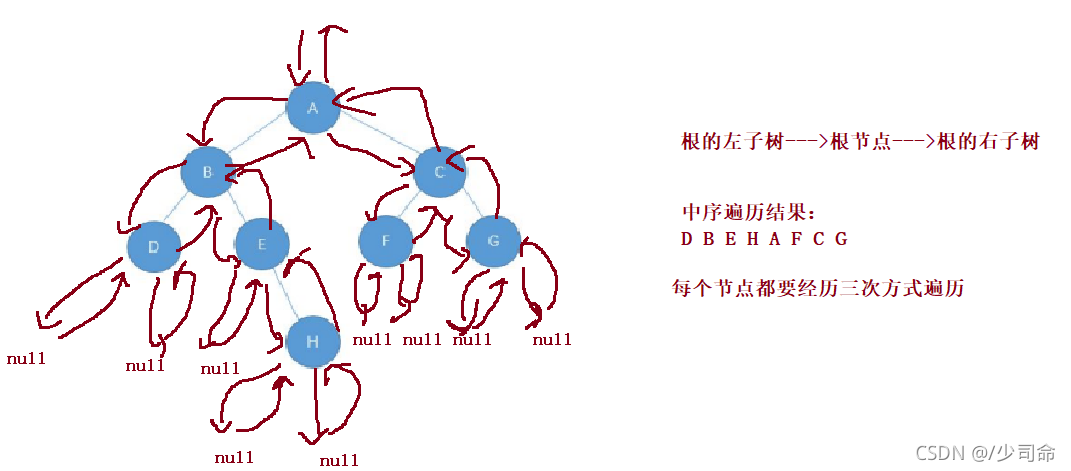
②二叉树中序遍历

?

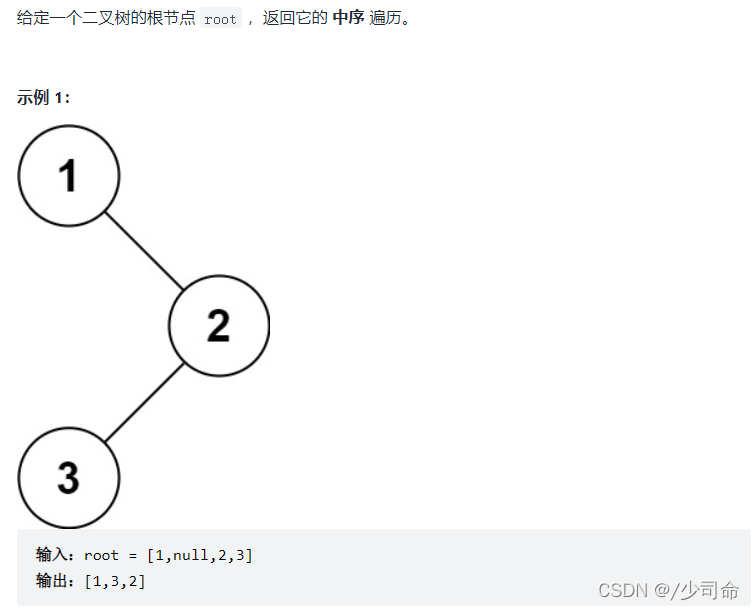
void inOrderTraversal(TreeNode root){
        if(root == null) {
            return;
        }
        inOrderTraversal(root.left);
        System.out.print(root.val+" ");
        inOrderTraversal(root.right);
    }

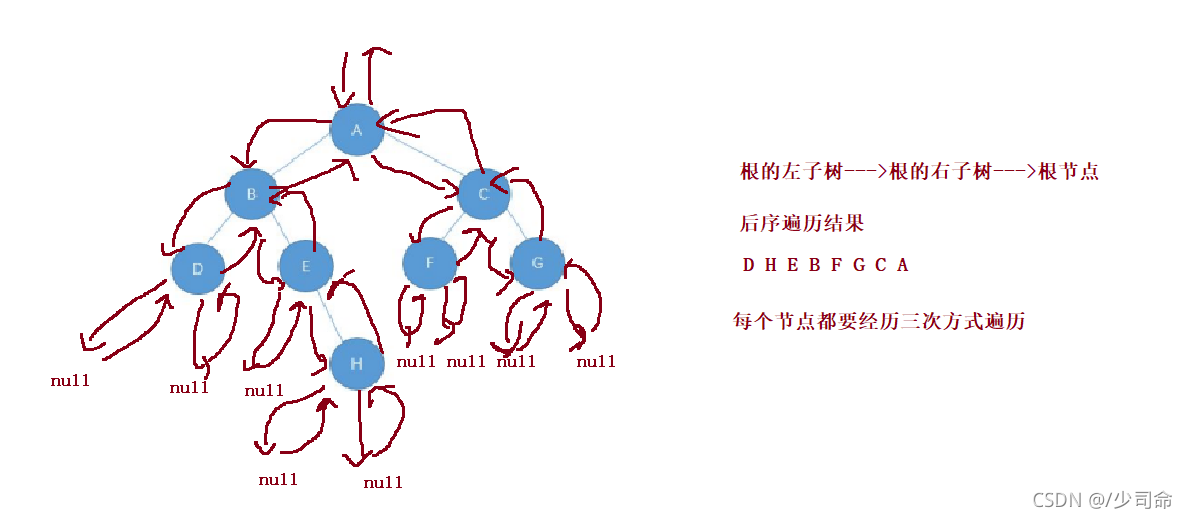
③二叉树后序遍历

?

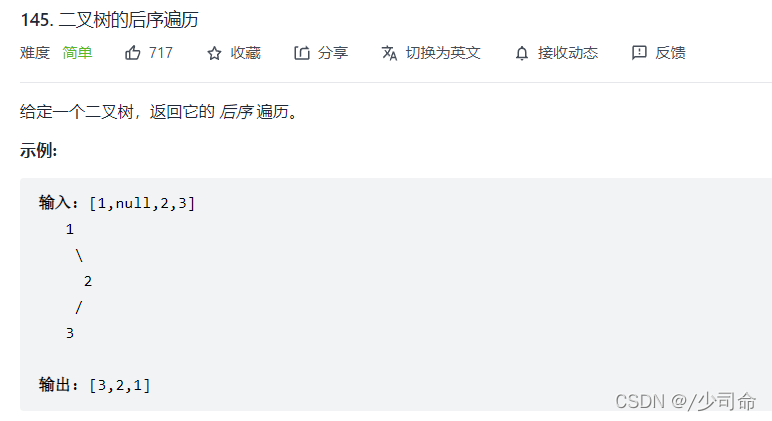
    void postOrderTraversal(TreeNode root){
        if(root == null) {
            return;
        }
        postOrderTraversal(root.left);
        postOrderTraversal(root.right);
        System.out.print(root.val+" ");
    }

④检查两棵树是否相同

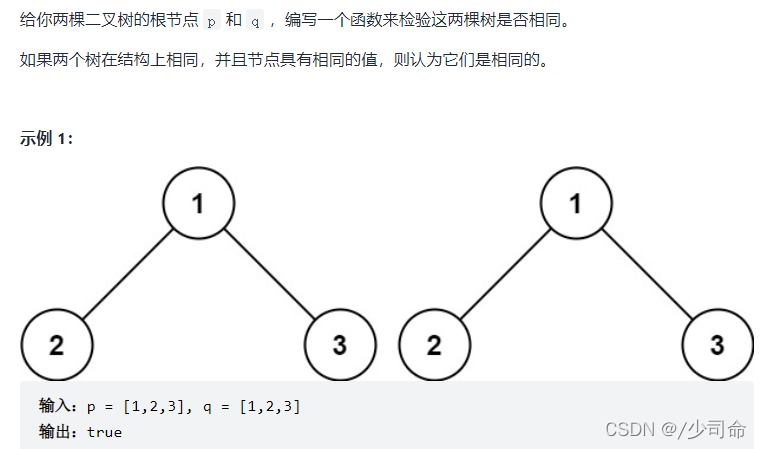
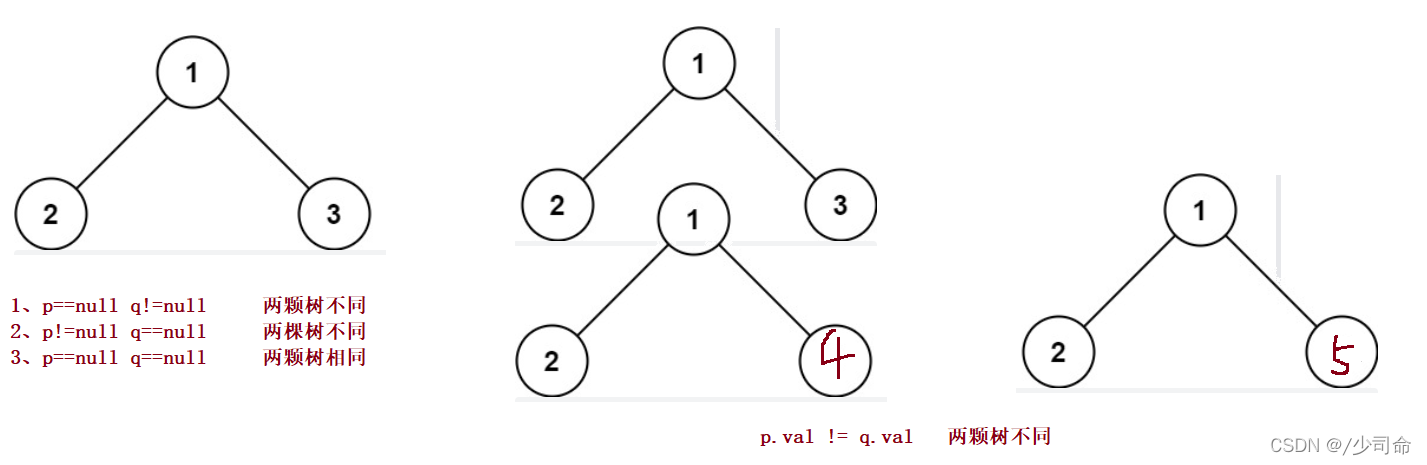
   public boolean isSameTree(TreeNode p,TreeNode q){
        if(p == null && q != null){
            return  false;
        }
        if(p != null && q == null){
            return  false;
        }
        if(p == null && q ==null){
            return true;
        }
        if(p.val != q.val){
            return false;
        }
        return  isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        
    }

⑤二茶树的最大深度

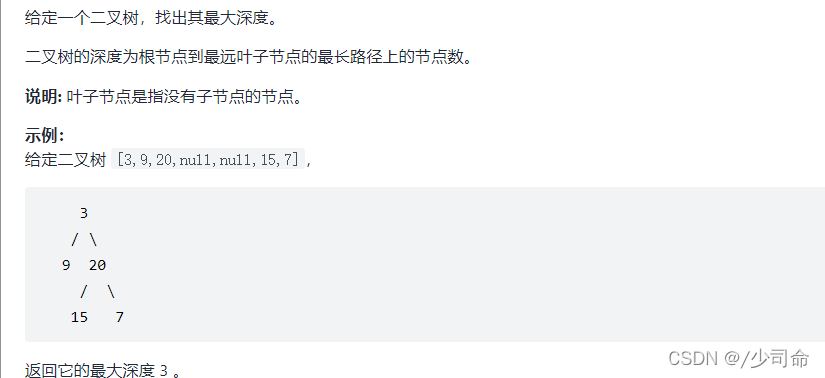
  public int maxDepth(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight =  maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return Math.abs(leftHeight-rightHeight > 0? leftHeight + 1: rightHeight + 1);
    }

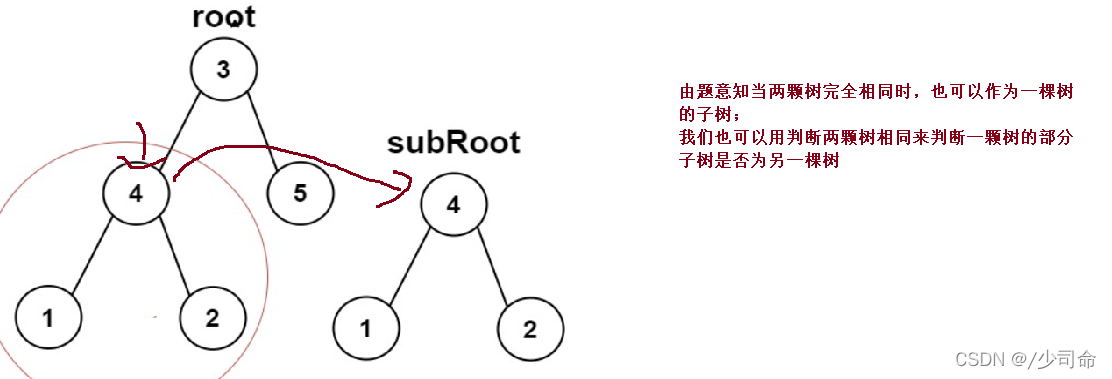
⑥另一颗树的子树

?

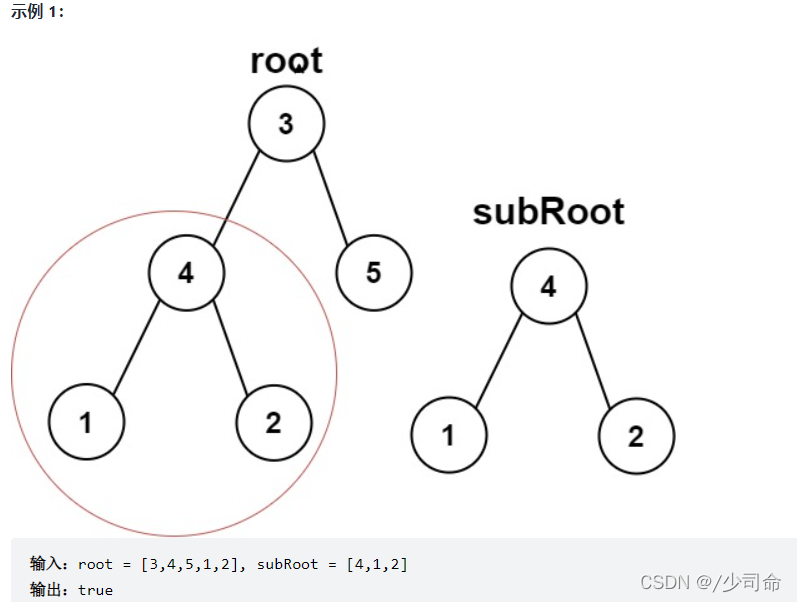
     public boolean isSameTree(TreeNode p,TreeNode q){
        if(p == null && q != null){
            return  false;
        }
        if(p != null && q == null){
            return  false;
        }
        if(p == null && q ==null){
            return true;
        }
        if(p.val != q.val){
            return false;
        }
        return  isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        
    }


    public boolean isSubtree(TreeNode root, TreeNode suBroot){
        if(root == null && suBroot == null){
            return true;
        }
        if(isSameTree(root,suBroot)){
            return true;
        }
        if(isSubtree(root.right,suBroot)){
            return true;
        }
        if(isSubtree(root.left,suBroot)){
            return true;
        }
        return false;
    }

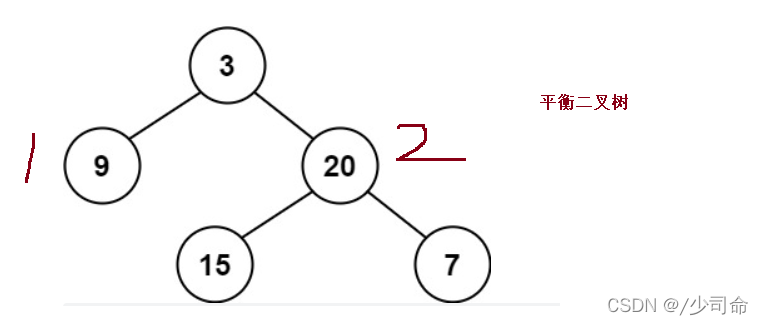
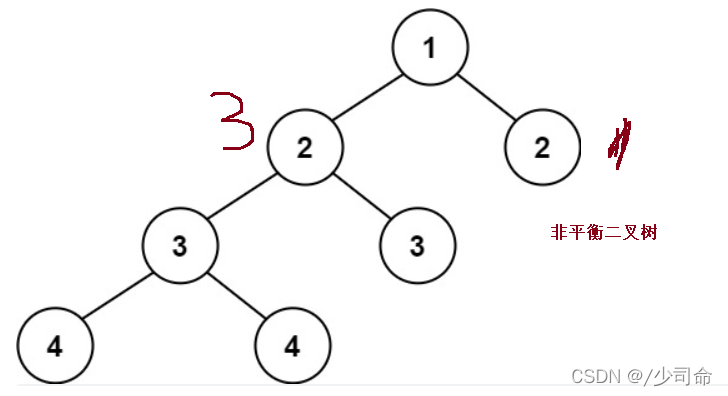
⑦判断一颗树是否为一颗平衡二叉树

???

?

?

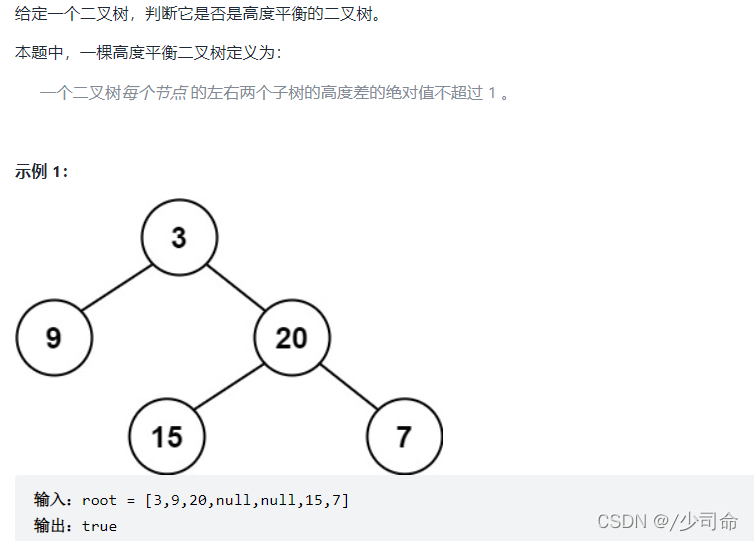
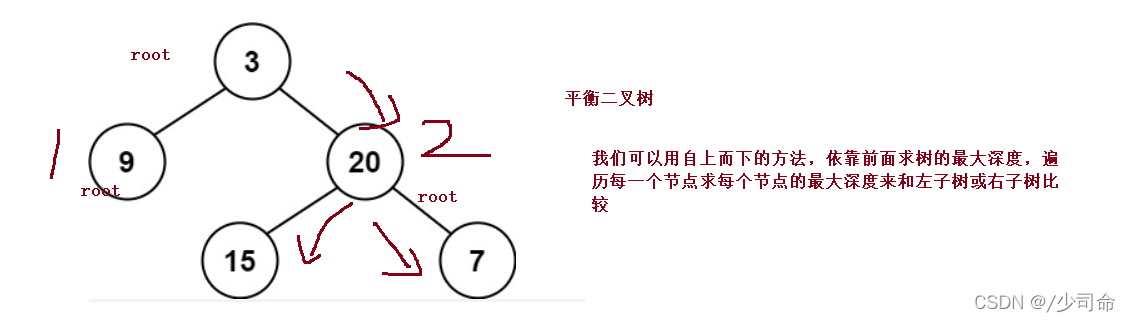
public int maxDepth(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight =  maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return Math.abs(leftHeight-rightHeight > 0? leftHeight + 1: rightHeight + 1);
    }

    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftHeight =  maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return
                Math.abs(leftHeight-rightHeight) < 2 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int hight(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight = hight(root.left);
        int rightHeight = hight(root.right);
        if(leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <= 1){
            return Math.max(leftHeight,rightHeight)+1;
        }else{
            return -1;
        }
    }
    public boolean isBalanced2(TreeNode root) {
        return hight(root) >= 0;
    }

⑧对称二叉树

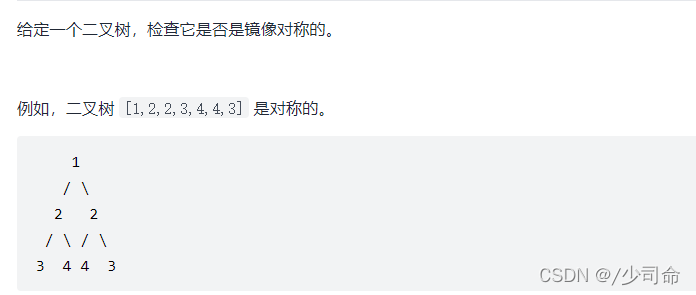
 public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
        if(leftTree != null && rightTree == null){
            return false;
        }
        if(leftTree == null && rightTree != null){
            return false;
        }
        if(leftTree == null && rightTree == null){
            return true;
        }
        if(leftTree.val != rightTree.val){
            return false;
        }
        return isSymmetricChild(leftTree.left,rightTree.right) &&
                isSymmetricChild(leftTree.left,rightTree.right);
    }
    public boolean isSymmetric(TreeNode root){
        if(root == null){
            return true;
        }
        return isSymmetricChild(root.left,root.right);
    }

⑨二叉树镜像

?

?

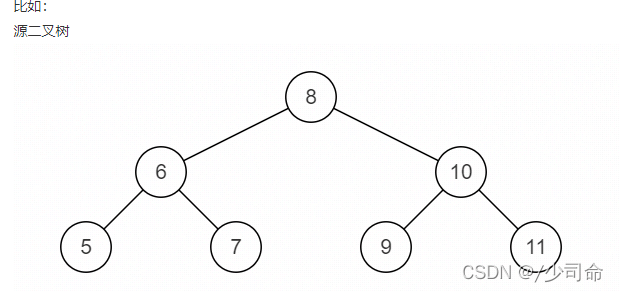
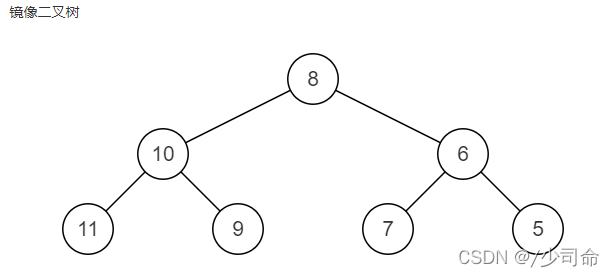
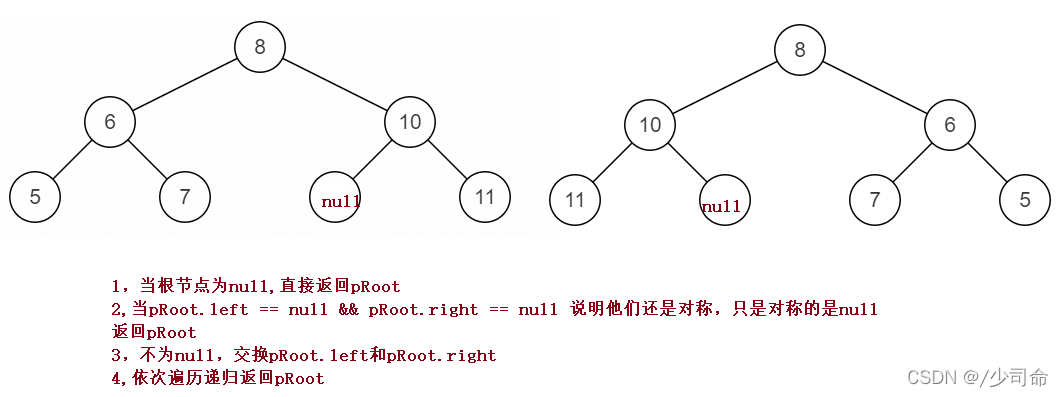
public TreeNode Mirror(TreeNode pRoot){
        if(pRoot == null){
            return pRoot;
        }
        if(pRoot.left == null && pRoot.right == null){
            return pRoot;
        }
        TreeNode tmp = pRoot.left;
        pRoot.left = pRoot.right;
        pRoot.right = tmp;
        
        if(pRoot.left != null){
            Mirror(pRoot.left);
            return pRoot;
        }
        if(pRoot.right != null){
            Mirror(pRoot.right);
            return pRoot;
        }
        return pRoot;
        
    }