二叉树的定义和基本术语
- 定义:二叉树是n(n>=0)个结点的有限集合;
当n=0时,为空二叉树;
由一个根节点和两个互不相交的称为根的左子树和右子树组成。左子树和右子树又分别是一颗二叉树 - 特点:
1.每个结点至多只有两棵子树
2.左右子树不能颠倒(二叉树是有序树)
3.即使树中某个结点只有一棵树,也要区分它是左子树还是右子树。
区别于度为2的树:至少有一个结点有两棵子树
- 二叉树的五种状态
1.空二叉树
2.只有左子树的二叉树
3.只有右子树的二叉树
4.只有根节点的二叉树
5.左右子树都有的二叉树
特殊的二叉树
斜树
左斜树:所有的结点都只有左子树的二叉树。
右斜树:所有的结点都只有右子树的二叉树。
满二叉树
所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上的二叉树。
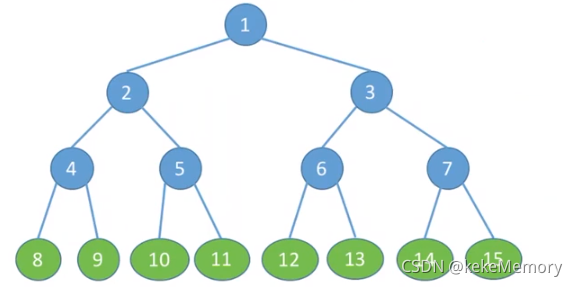
满二叉树特征
- 叶子结点只能出现在最下一层。出现在其他层就不可能达到平衡。
- 不存在度为1的结点,非叶子结点的度一定是2
- 根节点编号为
1,依次从上到下,从左至右给结点编号。结点i
的左孩子结点序号为2i,右孩子结点序号为2i+1。
完全二叉树
对于一颗具有n个结点的二叉树按层序编号,如果编号为i(1<=i&&i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同的二叉树。
完全二叉树特征
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左部连续位置。
- 倒数第二层,若有叶子结点,一定都在右部连续位置。
- 如果结点度为1,则该节点只有左孩子,即不存在只有右子树的情况。
- 同样结点的二叉树,完全二叉树的深度最小。
区分满二叉树和完全二叉树
满二叉树一定是完全二叉树。
完全二叉树不一定是满二叉树。
特征
- 只有最后两层可能有叶子结点
- 最多只有一个度为1的结点
- 根节点编号为
1,依次从上到下,从左至右给结点编号。结点i
的左孩子结点序号为2i,右孩子结点序号为2i+1。
二叉排序树
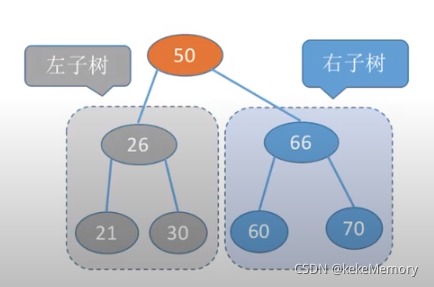
特征
左子树上所有结点的关键字均小于根节点的关键字右子树上所有结点的关键字均大于根节点的关键字
应用
二叉排序树可用于元素的排序和搜索
平衡二叉树
特征
- 树上任一结点的
左子树和右子树的深度之差不超过1 - 有更高的搜索效率
二叉树的性质
- 叶子结点比二分结点多一个
- 在二叉树的第i层上至多有
2^(i-1)个结点(i>=1) - 深度为k的二叉树至多有
2^k - 1个结点(k>=1)。(注意是2^k后再减去1) - 具有n个结点的完全二叉树的深度为:向下取整
log2n+1;(注意,对x的向下取整就是取不大于x的最大整数)
二叉树的存储结构
二叉树的顺序存储
- 二叉树的顺序存储中,一定要把二叉树的结点编号与完全二叉树对应起来
- 缺点:容易造成内存的空间浪费,因此二叉树的顺序存储结构只适合存储完全二叉树
#define MaxSize 100
//二叉树结点结构体定义
struct TreeNode{
ElemType value; //结点中的数据元素
bool isEmpty; //结点是否为空
};
//定义一个长度为MaxSize的数组t,用于静态顺序存储二叉树的各个结点
//如何布局存储?按照从上至下、从左至右的顺粗依次存储完二叉树的各个结点
TreeNode t[MaxSize];
//初始化
void IniTree(TreeNode t[MaxSize]){
for(int i=0;i<MaxSize;i++){
t[i].isEmpty=true; /*初始化时所有结点标记为空*/
}
}
二叉树的链式存储
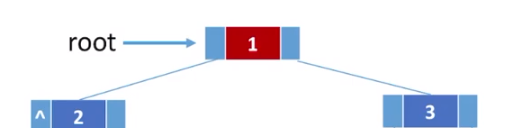
//二叉树的链式存储
struct ElemType{
int value; /*结点上的数据结构*/
}
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild; /*左右子结点*/
}BiTNode,*BiTree;
//定义一棵树 从根节点开始
BiTree root=NULL;
//插入根结点
root = (BiTree)malloc(sizeof(BiTNode)); /*申请内存空间给根节点*/
root->data={1};
root->lchild=NULL;
root->rchild=NULL;
//插入新的结点p
BiTNode *p =(BiTNode*)malloc(sizeof(BiTNode));
p->data={2};
p>lchild=NULL;
p->rchild=NULL;
root->lchild=p; /*新的结点p为根节点的左孩子*/
//插入新的结点q
BiTNode *q =(BiTNode*)malloc(sizeof(BiTNode));
q->data={3};
q>lchild=NULL;
q->rchild=NULL;
root->rchild=q; /*新的结点p为根节点的左孩子*/