复杂网络分析+代码实现
写在前面的话
关于图的相关笔记,仅供参考。
学习资料
复杂网络
随机网络:两个节点之间是否有边连接根据概率决定。
规则网络:两个节点之间是否有边连接是确定的。
复杂网络:绝大多数的实际网络并不是完全随机的,既不是规则网络,也不是随机网络,而是具有与前两者皆不同的统计特征的网络。
复杂网络的特性
具有自组织、自相似、吸引子(网络的内聚倾向)、小世界(相互关系的数目可以很小但却能够连接世界的事实)、无标度中部分或全部性质的网络称为复杂网络。
小世界特性
小世界特性(Small world theory):六度空间理论或者是六度分割理论(Six degrees of separation)。
六度空间理论:社交网络中的任何一个成员和任何一个陌生人之间所间隔的人不会超过六个。
特征路径长度(characteristic path length):在网络中,任选两个节点,连通这两个节点的最少边数,定义为这两个节点的路径长度,网络中所有节点对的路径长度的平均值,定义为网络的特征路径长度,这是网络的全局特征。
聚合系数(clustering coefficient):假设某个节点有k条边,则这k条边连接的节点(k个)之间最多可能存在的边的条数为k(k?1)/2,用实际存在的边数除以最多可能存在的边数得到的分数值,定义为这个节点的聚合系数。所有节点的聚合系数的均值定义为网络的聚合系数。聚合系数是网络的局部特征,反映了相邻两个人之间朋友圈子的重合度,即该节点的朋友之间也是朋友的程度。
性质
规则网络:任意两个点之间的特征路径长度长(通过多少点连在一起),但聚合系数高(共同邻居或共同间接邻居多)。
随机网络:任意两个点之间的特征路径长度短,但聚合系数低。
小世界网络:点之间特征路径长度小,接近随机网络,而聚合系数依旧相当高,接近规则网络。
实际影响
实际的社交、生态等网络都是小世界网络,这里面信息传递速度快,并且少量改变几个连接,就可以剧烈地改变网络的性能。
例如:蜂窝电话网,改动很少几条线路,就可以显著提高性能。
无标度特性
无标度网络:少数的节点拥有大量的连接,而大部分节点少,并且节点的度数分布符合幂率分布。
性质
异质性:其各节点之间的连接状况(度数)具有严重的不均匀分布性。
例如:网络中少数称之为Hub点的节点拥有极其多的连接,而大多数节点只有很少量的连接。少数Hub点对无标度网络的运行起着主导的作用。从广义上说,无标度网络的无标度性是描述大量复杂系统整体上严重不均匀分布的一种内在性质。
实际影响
无标度特性与鲁棒性:网络中的关键节点和链路往往成为攻击的对象。
社区结构特性
集群特性:复杂网络中普遍存在着聚类特性,每一个类称之为一个社团(community)。
例如,社会网络中总是存在熟人圈或朋友圈,其中每个成员都认识其他成员。
集群程度的意义:网络集团化的程度,这是一种网络的内聚倾向。
连通集团概念:一个大网络中各集聚的小网络分布和相互联系的状况。
例如,它可以反映这个朋友圈与另一个朋友圈的相互关系。
经典的复杂网络模型
经典网络模型的原理和构造方法,包括规则图,ER随机网络模型、BA无尺度网络模型和WS小世界模型。
规则图
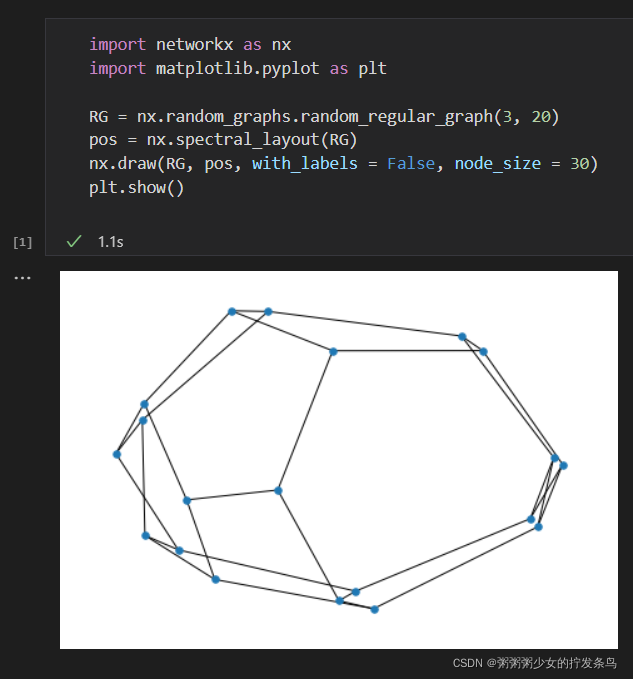
规则图:一个含有n个节点,每个节点有d个邻居节点的规则图。
import networkx as nx
import matplotlib.pyplot as plt
RG = nx.random_graphs.random_regular_graph(3, 20)
pos = nx.spectral_layout(RG)
nx.draw(RG, pos, with_labels = False, node_size = 30)
plt.show()
ER随机网络模型
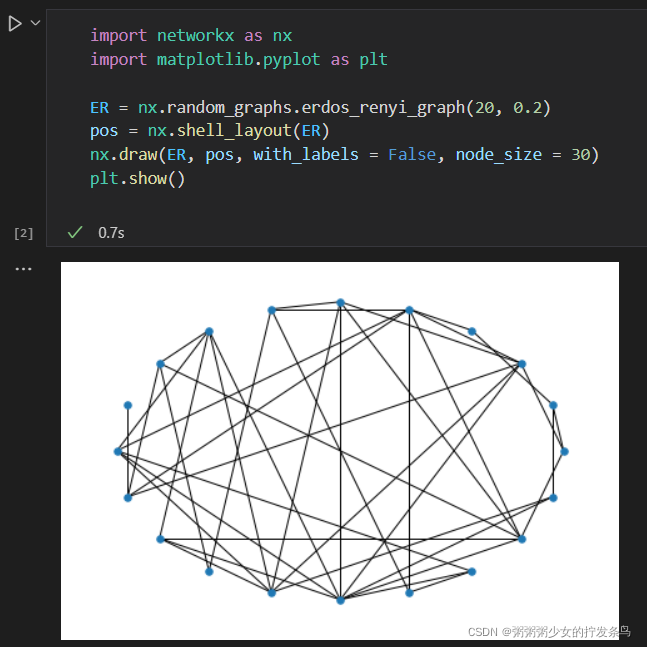
ErdOs-Renyi随机网络模型(ER):在网络节点间随机地布置连接,是个机会均等的网络模型.
import networkx as nx
import matplotlib.pyplot as plt
ER = nx.random_graphs.erdos_renyi_graph(20, 0.2)
pos = nx.shell_layout(ER)
nx.draw(ER, pos, with_labels = False, node_size = 30)
plt.show()
性质
户:给定一定数目的节点,它和其他任意一个节点之间有相互连接的概率相同。
因为一个节点连接k个其他节点的概率,会随着k值的增大而呈指数递减。
这样,如果定义是为每个节点所连接的其他节点的数目,可以知道连接概率p(k)服从钟形的泊松(Poisson)分布,有时随机网络也称作指数网络。
尽管连接是随机安置的,但由此形成的网络却是高度民主的,也就是说,绝大部分节点的连接数目会大致相同。实际上,随机网络中连接数目比平均数高许多或低许多的节点,都十分罕见。
实际影响
在过去40多年里,科学家习惯于将所有复杂网络都看作是随机网络。在1998年研究描绘万维网(以网页为节点、以超级链接为边)的项目时,学者们原以为会发现一个随机网络:人们会根据自己的兴趣,来决定将网络文件链接到哪些网站,而个人兴趣是多种多样的,可选择的网页数量也极其庞大,因而最终的链接模式将呈现出相当随机的结果。
然而,事实并非如此。因为在万维网上,并非所有的节点都是平等的。在选择将网页链接到何处时,人们可以从数十亿个网站中进行选择。然而,我们中的大部分人只熟悉整个万维网的一小部分,这一小部分中往往包含那些拥有较多链接的站点,因为这样的站点更容易为人所知。只要链接到这些站点,就等于造就或加强了对它们的偏好。这种“择优连接(Preferential Attachment)”的过程,也发生在其他网络中。在Internet上,那些具有较多连接的路由器通常也拥有更大的带宽,因而新用户就更倾向于连接到这些路由器上。在美国的生物技术产业内,某些知名公司更容易吸引到同盟者,而这又进一步加强了它在未来合作中的吸引力。类似地,在论文引用网络(论文为节点,引用关系为边)中,被引用次数较多的科学文献,会吸引更多的研究者去阅读并引用它。针对这些网络的“择优连接”的新特性,学者提出了BA无尺度网络模型。
BA无尺度网络模型
主要特征:节点的度分布服从幂次定律。
import networkx as nx
import matplotlib.pyplot as plt
BA = nx.random_graphs.barabasi_albert_graph(20, 1)
pos = nx.spring_layout(BA)
nx.draw(BA, pos, with_labels = False, node_size = 30)
plt.show()

性质
BA模型系统的成长性(Growth)和择优连接性。
BA模型的扩充可以考虑三个因素:择优选择的成本、边的重新连接、网络的初始状态。
实际影响
无尺度网络
1999年,丸Barabasi和兄Albert在对互联网的研究中发现了无尺度网络,使人类对于复杂网络系统有了全新的认识。过去,人们习惯于将所有复杂网络看作是随机网络,但Barabasi和Albert发现互联网实际上是由少数高连接性的页面组织起来的,80%以上页面的链接数不到4个。只占节点总数不到万分之一的极少数节点,却有1000个以上的链接。这种网页的链接分布遵循所谓的“幂次定律”:任何一个节点拥有是条连接的概率,与1/k成正比。它不像钟形曲线那样具有一个集中度很高的峰值,而是一条连续递减的曲线。如果取双对数坐标系来描述幂次定律,得到的是一条直线。
Scale-free网络指的是节点的度分布符合幂律分布的网络,由于其缺乏一个描述问题的特征尺度而被称为无尺度网络。其后的几年中,研究者们在许多不同的领域中都发现了无尺度网络。从生态系统到人际关系,从食物链到代谢系统,处处可以看到无尺度网络。
BA模型及其机制
为什么随机模型与实际不相符合呢?Barabasi和Albert在深入分析了ER模型之后,发现问题在于ER模型讨论的网络是一个既定规模的,不会继续扩展的网络。正是由于现实当中的网络往往具有不断成长的特性,早进入的节点(老节点)获得连接的概率就更大。当网络扩张到一定规模以后,这些老节点很容易成为拥有大量连接的集散节点。这就是网络的“成长性”。
其次,ER模型中每个节点与其他节点连接时,建立连接的概率是相同的。也就是说,网络当中所有的节点都是平等的。这一情况与实际也不相符。例如,新成立的网站选择与其他网站链接时,自然是在人们所熟知的网站中选择一个进行链接,新的个人主页上的超文本链接更有可能指向新浪、雅虎等著名的站点。由此,那些熟知的网站将获得更多的链接,这种特性称为“择优连接”。这种现象也称为“马太效应(Matthew Effect)”或“富者更富(Rich Get Richer)”。
“成长性”和“择优连接”这两种机制解释了网络当中集散节点的存在。
BA模型的改进方向
BA无尺度模型的关键在于,它把实际复杂网络的无尺度特性归结为增长和优先连接这两个非常简单的机制。当然,这也不可避免地使得BA无尺度网络模型和真实网络相比存在一些明显的限制。比如,一些实际网络的局域特性对网络演化结果的影响、外界对网络节点及其连接边删除的影响等。
一般自然的或者人造的现实网络与外界之间有节点交换,节点间连接也在不断变化,网络自身具有一定的自组织能力,会对自身或者外界的变化作出相应的反应。因此,在BA模型基础上,可以把模型的动力学过程进行推广,包括对网络中已有节点或者连接的随机删除及其相应的连接补偿机制。
对每一个时间步长,考虑如下三种假设:
1、成长假设:一个带有m个择优连接的新节点加入网络,这个新节点选择网络中m个节点,即对于每一个连接,一个度为是的节点作为目标
被选择的概率正比于k;
2、删除假设:考虑网络中若干个节点,这些节点与其他节点之间的连接边被随机地选作目标边而被删除,导致网络的演化;
3、补偿假设:网络中失去一个连接,同时产生n个连接进行补偿,其中”有上确界,是一个受网络补偿能力限制的量,这里的补偿连接所选择的目标节点也遵循择优连接原则。
利用以上三种假设,很多学者已经对BA模型进行了有效的改进,读者可参考相关文献,此处不再详述。
小世界网络模型
“小世界现象”/“六度分离(Six Degrees of Separation)”:绝大多数大规模真实网络的平均路径长度比想象的小得多。
小世界现象:每个人只需要很少的中间人(平均6个)就可以和全世界的人建立起联系。
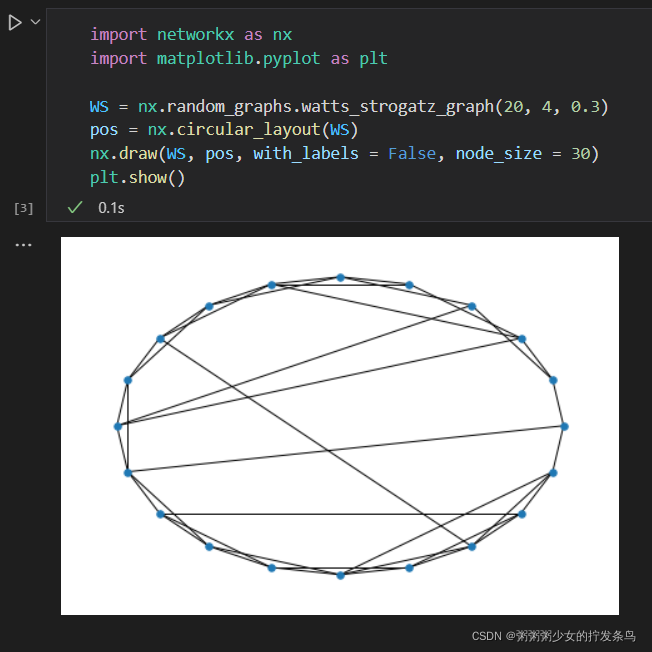
WS小世界模型:介于规则网络和完全随机网络之间的单参数小世界网络模型,该模型较好地体现了社会网络的小平均路径长度和大聚类系数两种现象。
import networkx as nx
import matplotlib.pyplot as plt
WS = nx.random_graphs.watts_strogatz_graph(20, 4, 0.3)
pos = nx.circular_layout(WS)
nx.draw(WS, pos, with_labels = False, node_size = 30)
plt.show()
WS小世界模型构造
从规则图开始,考虑一个含有N个节点的规则网络,它们圈成一个环,其中每个节点都与它左右相邻的各K/2个节点相连接,K为偶数;
随机化重连,以概率户随机地重新连接网络中的每条边(将边的一个端点保持不变,而另一个端点取为网络中随机选择的一个节点),其中规定,任意两个不同的节点之间至多只能有一条边,并且每一个节点都不能有边与其自身相连。
在WS小世界模型中,p=0对应于规则网络,p=l则对应于完全随机网络,通过调节声的值就可以控制从规则网络到完全随机图的过渡。因此,WS小世界网络是介于规则网络和随机网络之间的一种网络。
WS小世界模型构造算法中的随机化过程有可能破坏网络的连通性。
NW小世界模型构造
从规则图开始,考虑一个含有N个点的规则网络,它们圈成一个环,其中每个节点都与它左右的相邻的各K/2节点相连,K是偶数;
随机化加边,以概率p随机选取的一对节点之间加上一条边。其中规定,任意两个不同的节点之间至多只能有一条边,并且每一个节点都不能有边与自身相连。
NW模型只是将WS小世界模型构造中的“随机化重连”改为“随机化加边”。
NW和WS的区别
NW模型不同于WS模型之处在于它不切断规则网络中的原始边,而是以概率p重新连接一对节点。这样构造出来的网络同时具有大的聚类数和小的平均距离。
NW模型的优点在于其简化了理论分析,因为WS模型可能存在孤立节点,但NW模型不会。当户足够小和N足够大时,NW小世界模型本质上就等同于WS小世界模型。
实际影响
小世界网络模型反映了实际网络所具有的一些特性,例如朋友关系网,大部分人的朋友都是和他们住在同一个地方,其地理位置不是很远,或只在同一单位工作或学习的同事和同学。另一方面,也有些人住得较远的,甚至是远在异国他乡的朋友,这种情形好比WS小世界模型中通过重新连线或在NW小世界模型中通过加入连线产生的远程连接。
小世界网络模型的主要特征之一是节点之间的平均距离随远程连接的个数而指数下降。对于规则网络,平均距离L可估计为L正比于N;而对于小世界网络模型,L正比于ln(N)/1n(K)。例如,对于一个千万人口的城市,人与人的平均接触距离是6左右,这使得生活人群之间的距离大大缩短。该模型由一个规则的环组成,通常是一个一维的几乎具有周期性边界条件的环(即环中每个节点几乎都连接到一固定数目的邻近节点)和少量的随机选取节点连接成的“捷径” (重新连接现存的边)。小世界网络同时具有“高网络聚集度”和“低平均路径”的特性。
从小世界网络模型中可以看到,只要改变很少的几个连接,就可以剧烈的改变网络的性能。这样的性质也可以应用其他网络,尤其是对已有网络的调整方面。例如,蜂窝电话网,改动很少几条线路(低成本、低工作量)的连接,就可以显著提高性能。也可以应用到互联网的主干路由器上,以改变流量和提高传输速度。同样的思路也可以应用到电子邮件的快速传递、特定Web站点的定位等。