[数据结构与算法]最长公共子序列（leetcode1143题）

题目描述
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

解题要点
该题使用动态规划的方法，要先找出状态转移方程

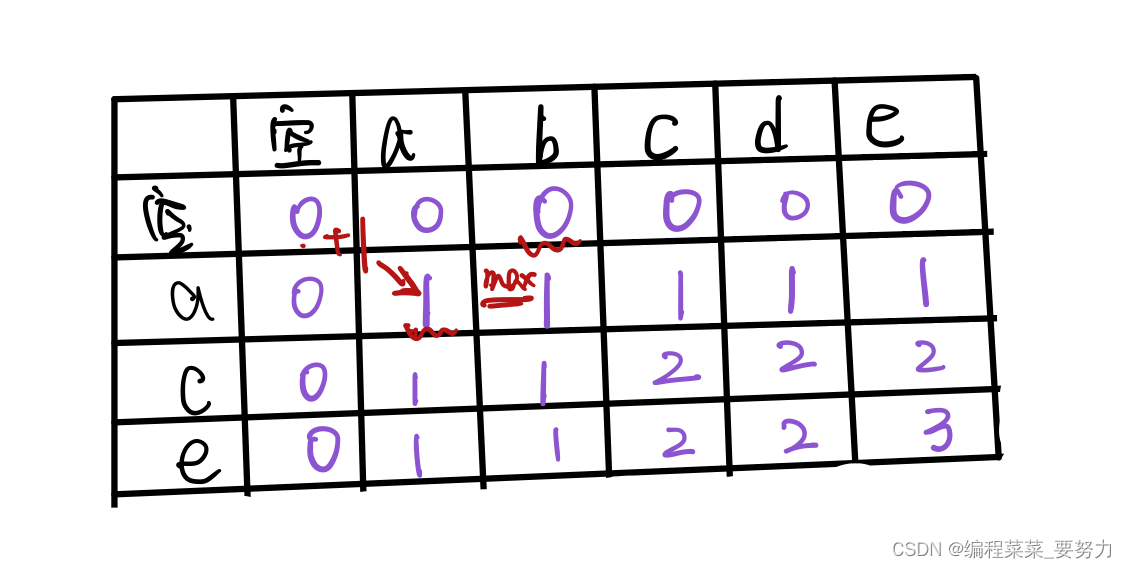
画图如下所示，如果两个字符串 str1=“abcde”, str2=“ace”，将两个字符串写到表格的行列中
1）每个字符和空字符公共长度为0
2）从左上角开始，
如果行列两个字符相同，到该字符为止的最长公共子序列=左上角数字+1；
如果不同，到该字符为止的公共子序列=max(左，上) + 1

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size();
        int n = text2.size();
        vector<vector<int>> dp(m+1, vector<int>(n+1)); //根据上图创建矩阵
        for(int i = 1; i <= m; ++i) { // i,j的设计按照dp来
            char c1 = text1[i-1]; // 此处注意是i-1（dp下标从1开始，字符串下标从0开始）
            for(int j = 1; j <= n; ++j) {
                char c2 = text2[j-1]; // 此处注意是j-1
                if(c1==c2) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
                
            }

        }
        return dp[m][n];    
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn) , 因为创建了二维数组

动态规划
是一种解决问题的思想，大规模问题的结果，是由小规模问题的结果运算得来的。动态规划可用递归来实现。
主要关注：状态，状态转移方程 （每个位置的结果可以由之前位置而来–》用动态规划–》重点要写出来【动态规划方程（即找出规律）】）