数据结构
定义
什么是数据结构呢,其实这并没有一个统一的定义。
在《数据结构(C语言版)》中是这样定义的:
数据结构是一门研究非数值计算的程序设计问题中计算机的操作对象以及它们之间的关系和操作等的学科。
在老师给的PPT上的定义:
数据结构是一门讨论“描述世界实体的数学模型(非数值计算)以及其上的操作在计算机中如何表示和实现”的学科。
而MOOC上的《数据结构》课程则是这样说的:
数据对象在计算机中的组织方式分为逻辑结构、物理存储结构。
数据对象必定与一系列加在其上的操作相关联在数据结构中通常使用抽象数据类型
数据类型分为数据对象集、数据集合相关联的操作集
抽象:描述数据类型的方法不依赖于具体实现
只描述数据对象集和相关操作集“是什么”,并不涉及“如何做到”这个问题。
这段话还蛮绕的,在我看来吧,数据结构一来是让我们学习一种解决问题的思想,主要是数据的创建、删除、插入、查找、释放。这门课并不涉及具体的代码实现;二来是教我们如何为解决一个问题而为问题中的数据构造一种结构模型,比如线性表、图、树、队列、栈之类的。(说的有失偏颇,可以跳过这段。。。不过学习过程中的确有这样的感觉)
解决问题方法的效率,和数据的组织方式有关。
就比如,现在有一组数据,要求你查找某一个数据在该数据集中的位置。
如果这组数据是随便放的,你查找起来会很麻烦吧。
如果这组数据是按照从小到大的顺序排放的,那查找起来就会简单许多了。
这组数据的放置方式就是数据的组织方式。
解决问题方法的效率,和空间的利用效率有关。
例如,写一个程序实现函数PrintN,使得传入一个正整数为N的参数后,能顺序打印从1到N的全部正整数
循环实现
void PrintN(int N){
int i;
for(i=1;i<=N;i++)
printf("%d\n",i);
}
递归实现
void PrintN(int N){
if(N){
PrintN(N-1);
printf("%d\n",N);
}
}
使用递归的话很占空间内存,因为每递归一次都要开辟新的空间来存储递归前的函数
而循环则是一开始就固定了空间。
当我输入100000时,用递归时编译器就不堪重负,罢工了。
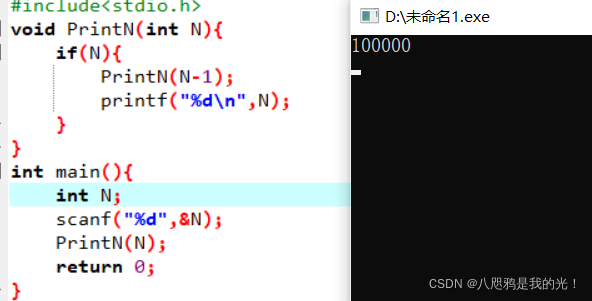
输入完就没了
而循环则没有这个问题。
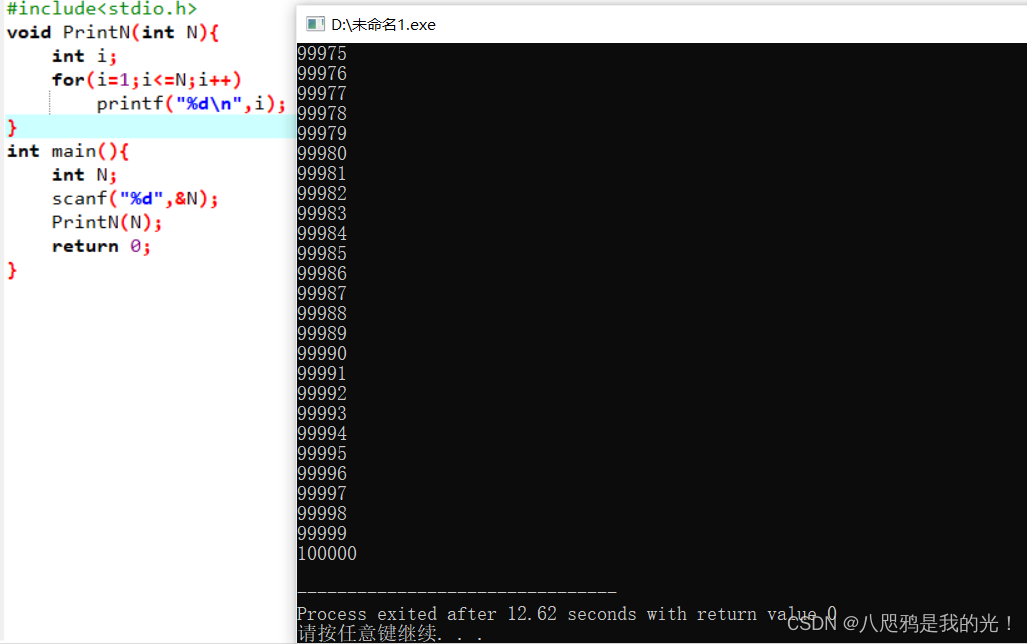
(只截取了结尾处 )
解决问题方法的效率,跟算法的巧妙程度有关
例如:写程序计算给定多项式在给定点x处的值
f(x)=a0+a1乘x+a2乘x^2+……+an乘x的n次方
方法一:
double f1(int n,double a[],double x){
double p=a[0];
for(int i=1;i<=n;i++)
p+=(a[i]*pow(x,i));
return p;
}
方法二
整理一下这个多项式:
f(x)=a0+x(a1+x(……(an-1 +x(an))……))
double f2(int n,double a[],double x){
double p=a[n];
for(int i=n;i>0;i--)
p=a[i-1]+x*p;
return p;
}
方法二明显比方法一跑得快
术语
数据:
所有能被输入到计算机中,且能被计算机处理的符号(数字、字符、图像、声音等)的集合。是计算机操作的对象的总称。是计算机处理的信息的某种特定的符号表示形式。
数据元素
是数据(集合)中的一个“个体”,是数据结构中讨论的基本单位。
数据项是不可再分割的“原子”。是数据结构中讨论的最小单位。
关键字(KEY)
能识别一个或几个数据元素的数据项。若能起唯一识别作用,则被称为“主”关键字,否则称为“次”关键字。
数据对象
具有相同特性的数据元素的集合,是数据的一个子集(比如整数、实数就是数据对象)。
数据结构
定义
有一个特性相同的数据元素的集合,如果在数据元素之间存在一种或多种特定的关系,则称为一个数据结构。
整理一下:数据结构就是相互之间存在着某种逻辑关系的数据元素的集合。
形式定义:
数据结构是一个二元组
Data_Structures=(D,S)
D指的是数据元素的有限集
S是D上关系的有限集
分类
从关系或结构上分,数据结构可以分为:
-
线性结构
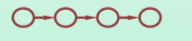
-
树形结构
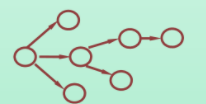
-
图状结构
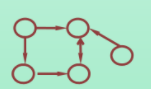
-
集合结构

层次划分
数据结构包括“逻辑结构”和“物理结构”两个方面
逻辑结构
是对数据元素之间逻辑关系的描述,它可以用一个数据元素的集合和定义在此集合上的诺肝关系来表示
物理结构(存储结构)
是逻辑结构在计算机中的表示和实现
是逻辑结构在存储器中的映象
存储结构中只包含数据元素本身的信息
“关系”的两种映象方法(表示<x,y>的方法)
顺序映象:以x和y之间相对的存储位置表示后继关系
链式映象:以附加信息(指针)表示后继关系,需要用一个和x绑定在一起的附加信息指示y的存储位置【以“由数据元素x的存储映象和附加的指针合成的结点”表示数据元素】
数据类型
是一个值的集合和定义在此集合上的一组操作的总称。(说的太玄乎了,就像是c语言中的基本数据类型int,float,double之类的)
抽象数据类型(ADT)
是指一个数学模型以及定义在此数学模型上的一组操作。
ADT的两个重要特征
数据抽象
强调其本质的特征、其所能完成的功能以及它和外部用户的接口。(就是外界使用它的方法)
数据封装
将实体的外部特性和其内部实现细节分离,并且对外部用户隐藏其内部实现细节。
ADT的描述方法
ADT=(D,S,P)
D:数据对象
S:D上的关系
P:对D的基本操作集
算法
定义
算法是为了解决某类问题而规定的一个有限长的操作序列。
MOOC上说的是
一个有限指令集
接受一些输入(有些情况下不需要输入)
产生输出
一定在有限步骤之后终止
每条指令必须有充分明确的目标,不可以有歧义;必须在计算机能处理的范围内;描述不依赖于任何一种计算机语言以及具体的实现手段。
特性
有穷性(有穷步骤,有限时间)
确定性
可行性
有输入(有的算法表面上没有输入,但实际上已被嵌入到算法中了)
有输出
算法设计的原则
正确性
可读性
健壮性
高效率与低存储量需求(效率指的是算法执行时间,存储量指的是算法执行过程中所需的最大存储空间)
算法效率的衡量方法和准则
方法
事后统计法
缺点:1.必须要执行程序2.可能会存在其他因素掩盖算法本质
事前分析估算法
优点:可以预先比较各种算法
和算法执行时间相关的因素
- 算法选用的策略
- 问题的规模(影响“运行工作量”的大小)
- 编写程序的语言
- 编译程序产生的机器代码的质量
- 计算机执行指令的速度
算法的存储空间需求
算法的存储量包括:
- 输入数据所占空间
- 程序本身所占空间
- 辅助变量所占空间
若输入数据所占空间只取决于问题本身,和算法无关,则只需要分析除输入和程序之外的辅助变量所占额外空间。
如果所需额外空间相对于输入数据量来说是常数,则称此算法为原地工作。
应用实例
来自MOOC
最大子列和问题
问题描述
给定N个整数的序列{A1,A2,……,AN},求函数f(i,j)=max{0,A1+A2+……+AN}
算法一:暴力枚举(三重循环) 时间复杂度O(n^3)
int MaxSubseqSum1(int A[],int N){
int ThisSum,MaxSum=0;
int i,j,k;
for(i=0;i<N;i++){/*i是子列左端位置*/
for(j=i;j<N;j++){/*j是子列右端位置*/
ThisSum=0;
for(k=i;k<=j;k++)
ThisSum+=A[k];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
}
}
return MaxSum;
}
算法二:较为简化(两重循环)时间复杂度O(n^2)
int MaxSubseqSum2(int A[],int N){
int i,j;
for(i=0;i<N;i++){
ThisSum=0;
for(j=i;j<N;j++){
ThisSum+=A[j];
/*对于相同的i,不同的j,只要在j-1次循环的基础上累加1*/
if(ThisSum>MaxSum)
MaxSum=ThisSum;
}
}
return MaxSum;
}
算法三:分而治之 时间复杂度O(nlogn)
算法四:在线处理 时间复杂度O(n)
int MaxSubseqSum4(int A[],int N){
int ThisSum,MaxSum;
int i;
ThisSum=MaxSum=0;
for(i=0;i<N;i++){
ThisSum+=A[i];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
else if(ThisSum<0)
ThisSum=0;
}
return MaxSum;
}