【题目链接】
【前置知识】
这题是一道树形
d
p
dp
dp 的模板题,我们要用到一种新的存储结构——链式前向星。
首先我们先来了解一下链式前向星的原理
利用链式储存结构。对于每一个顶点,开一条链,依次存储以该点为起点的边。
————PPT
那我们应该如何实现呢?
首先,我们需要一个结构体数组
e
e
e,用这个数组来存储边的信息,其中我们需要存储三个信息:
e
x
e_x
ex? 当前点,
e
y
e_y
ey? 所连接的点,
e
n
e
x
t
e_{next}
enext? 所连接的点的下一个点
struct NOTE
{
int x,y,next;
}e[N];
下面是如何建边,我们还需要有一个数组
h
e
a
d
head
head。
h
e
a
d
i
head_i
headi? 存储
i
i
i 这个顶点对应的链的起始位置。
void add(int x,int y)//两个点之间建边
{
e[++tot].x=x;//存当前点
e[tot].y=y;//它所连接的点
e[tot].next=head[x];//x上一个点的位置
head[x]=tot;//它上一个点的位置在哪里
}
借助题目数据来理解一下
1 3
2 3
6 4
7 4
4 5
3 5
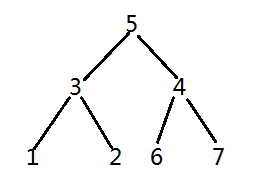
给出一张表方便理解这个过程

【过程】
第一次是1 3建边
e
x
=
3
e_x=3
ex?=3
e
y
=
1
e_y=1
ey?=1
因为它是这条链的起点所以
e
n
e
x
t
=
0
e_{next}=0
enext?=0
h
e
a
d
3
=
1
head_3=1
head3?=1
第二次是2 3建边
e
x
=
3
e_x=3
ex?=3
e
y
=
2
e_y=2
ey?=2
e
x
=
3
e_x=3
ex?=3 链接这
1
1
1 这个位置
e
n
e
x
t
=
1
e_{next}=1
enext?=1
h
e
a
d
3
=
2
head_3=2
head3?=2 链接的位置移到了这里
第三次是6 4建边
e
x
=
4
e_x=4
ex?=4
e
y
=
6
e_y=6
ey?=6
因为它是这条链的起点所以
e
n
e
x
t
=
0
e_{next}=0
enext?=0
h
e
a
d
4
=
3
head_4=3
head4?=3
第四次是7 4建边
e
x
=
4
e_x=4
ex?=4
e
y
=
7
e_y=7
ey?=7
e
x
=
4
e_x=4
ex?=4 链接这
3
3
3 这个位置
e
n
e
x
t
=
3
e_{next}=3
enext?=3
h
e
a
d
4
=
4
head_4=4
head4?=4 链接的位置移到了这里
第五次是4 5建边
e
x
=
5
e_x=5
ex?=5
e
y
=
4
e_y=4
ey?=4
因为它是这条链的起点所以
e
n
e
x
t
=
0
e_{next}=0
enext?=0
h
e
a
d
5
=
5
head_5=5
head5?=5
第六次是3 5建边
e
x
=
5
e_x=5
ex?=5
e
y
=
3
e_y=3
ey?=3
e
x
=
5
e_x=5
ex?=5 链接这
5
5
5 这个位置
e
n
e
x
t
=
5
e_{next}=5
enext?=5
h
e
a
d
5
=
6
head_5=6
head5?=6 链接的位置移到了这里
【注意事项】
最后注意一下:这里是因为题目说了
每行输入一对整数 l, kl,k,代表 kk 是 ll 的直接上司
所以只需要建一次边,但是当这个图是无向时,我们还需要正反建两次边。
【解题思路】
言归正传,我们来讲一下这道题到底怎么做?
这道题我们需要用到一些分类讨论的思想。
定义
d
i
,
0
d_{i,0}
di,0? 为不选第
i
i
i 个节点的最大的快乐指数
d
i
,
1
d_{i,1}
di,1? 为选第
i
i
i 个节点的最大的快乐指数
如果选这个节点,那么它的子节点一定不能选,则
d
i
,
1
=
d
j
,
0
d_{i,1}=d_{j,0}
di,1?=dj,0?
如果不选这个节点,那么它的子节点可选可不选,则
d
i
,
1
=
m
a
x
(
d
j
,
0
,
d
j
,
1
)
d_{i,1}=max(d_{j,0},d_{j,1})
di,1?=max(dj,0?,dj,1?)
动态转移方程
d
i
,
k
=
{
d
j
,
0
k
=
0
m
a
x
(
d
j
,
1
,
d
j
,
0
)
k
=
1
d_{i,k}=\begin{cases} d_{j,0}&k=0\\ max(d_{j,1},d_{j,0})&k=1 \end{cases}
di,k?={dj,0?max(dj,1?,dj,0?)?k=0k=1?
【CODE】
#include<iostream>
#include<cstdio>
using namespace std;
int head[6010],d[6001][2];
int h[6010],v[6010];
int n,tot,xx,yy,maxn=-0x7ffffff,gen;
struct note
{
int x,y,nxt;
}e[6010];
void add(int x,int y)
{
e[++tot].x=x;
e[tot].y=y;
e[tot].nxt=head[x];
head[x]=tot;
}
void dp(int nw)
{
d[nw][1]=h[nw];//初始化选自己
for (int i=head[nw];i;i=e[i].nxt)//序号,往链表的前面找
{
dp(e[i].y);//子节点
d[nw][1]=d[e[i].y][0]+d[nw][1];//dp
d[nw][0]=max(d[e[i].y][1],d[e[i].y][0])+d[nw][0];
}
}
int main()
{
cin>>n;
for (int i=1;i<=n;i++)
cin>>h[i];
for (int i=1;i<n;i++)
{
cin>>xx>>yy;
add(yy,xx);//两个点之间建一条边
v[xx]=1;//这个点为子节点
}
//找根节点
for (int i=1;i<=n;i++)
if (v[i]==0)
{
gen=i;
break;
}
dp(gen);//从根节点开始搜索
cout<<max(d[gen][0],d[gen][1]);//选较大的输出
return 0;
}