[数据结构与算法]计算方法上(Java)

一、绪论

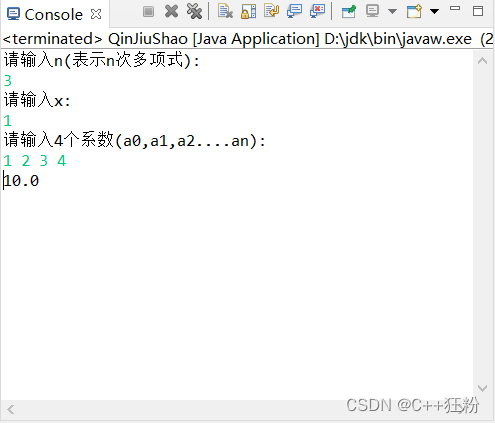
1. 秦九韶算法

$$a_0+a_{1}x+a_2{x}^2+a_3{x}^3=\left(\left(a_{3}x+a_2\right)x+a_1\right)x+a_0$$

package Abstract;
//秦九韶算法
import java.util.Scanner;

public class QinJiuShao {
	public static void main(String[] args) {
		int n;
		double x;
		Scanner scan=new Scanner(System.in);
		System.out.println("请输入n(表示n次多项式):");
		n=scan.nextInt();
		System.out.println("请输入x:");
		x=scan.nextDouble();
		double[] Xishu=new double[n+1];
		System.out.printf("请输入%d个系数(a0,a1,a2....an):\n",n+1);
		for(int i=0;i<n+1;++i) {
			Xishu[i]=scan.nextDouble();
		}
		double ans=Xishu[n];
		for(int i=n-1;i>=0;--i) {
			ans=ans*x+Xishu[i];
		}
		System.out.println(ans);
	}
}

2. 二分法求方程的实根

package Abstract;
//二分法求方程的实根
public class BinaryRoot {
	public static double getValue(double x) {
		return Math.exp(x)+10*x-2;
	}
	public static double binaryRoot() {//不具有普遍性，只是针对方程y=e^x+10x-2,在区间[0,1]上
		double left=0;
		double right=1;
		double mid=left+(right-left)/2;
		while(left<=right) {
			if(right-left<=0.005)return mid;
			else if(getValue(left)*getValue(mid)<0) {
				right=mid;
				mid=left+(right-left)/2;
			}
			else {
				left=mid;
				mid=left+(right-left)/2;
			}
		}
		return -1;//表示没有根
	}
	public static void main(String[] args) {
		double root=binaryRoot();
		System.out.println("方程y=e^x+10x-2在[0,1]上的实根为 "+root);
	}
}

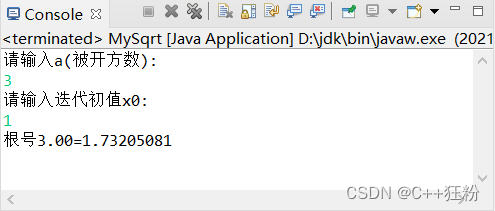
3. 迭代法求开方

package Abstract;

import java.util.Scanner;

//开方,有已得到证明的迭代公式
public class MySqrt {
	public static void main(String[] args) {
		Scanner scan=new Scanner(System.in);
		double a;//求根号a的值
		System.out.println("请输入a(被开方数):");
		a=scan.nextDouble();
		double x0;
		System.out.println("请输入迭代初值x0:");
		x0=scan.nextDouble();
		double x1=x0;
		do {
			x0=x1;
			x1=0.5*(x0+a/x0);
			
		}while(Math.abs(x1-x0)>=1e-6);
		System.out.printf("根号%.2f=%.8f\n",a,x0);
	}
}

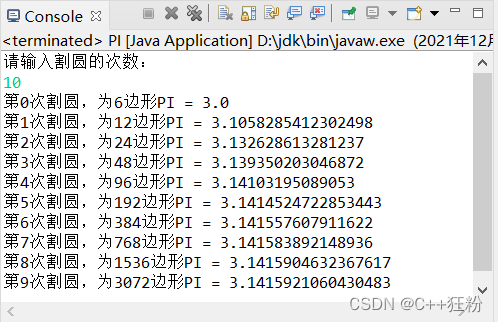
4. 割圆术

package Abstract;

import java.util.Scanner;

//割圆术
public class PI {
	public static void main(String[] args) {
		int i,n,s;
		double k,y2;
		System.out.println("请输入割圆的次数：");
		Scanner scanner = new Scanner(System.in);
		if(scanner.hasNext()) {
			n = scanner.nextInt();
			i = 0;
			k = 3.0;
			y2 = 1.0;
			s = 6;
			while(i<n) {
				System.out.println("第"+i+"次割圆，为"+s+"边形"+"PI = "+k*Math.sqrt(y2));
				s*=2;
				y2=2-Math.sqrt(4-y2);
				i++;
				k*=2.0;
			}
		}
	}

}