1.来源
? 当数据比较大,无法全部存入内存时,需要将部分数据存在外存中,在需要的时候读入内存,修改之后又写回外存。由于外存的速度与内存有几个数量级的差别,所以想要节省在外存上花的时间,必须提高搜索树的性能。
?最常见的外存就是磁盘。磁盘是快设备,也就是说磁盘的读写单位是以块为单位,一般地块大小从0.5k到4k。即使你只读取一个字节,磁盘也是将包含该字节的所有数据读取到硬盘中。而在磁盘读取过程中,最占用时间的是磁盘的寻道,也就是磁头在盘片上找到需要读取的块所在位置的时间,而在盘片上顺序读取数据的所花的时间是占比比较小的。
?要减少外存上花的时间,就可以从减少读盘次数以及减少寻道时间着手。
?B树采取的方法就是,就充分的利用盘块的空间,在一个盘块中尽可能多的存储信息,或者在连续的盘块地址上存储尽可能多的信息。在数据结构上的变化就是每个结点存储多个key信息以及包含多个子结点。增加结点的分支树,就可以使得这棵树的高度降低,比如高度为2(root高度为0)分支1000的数,就以存储10001000个关键字信息,而二叉树j的高度就至少需要6ln10。
?举一个具体的栗子:
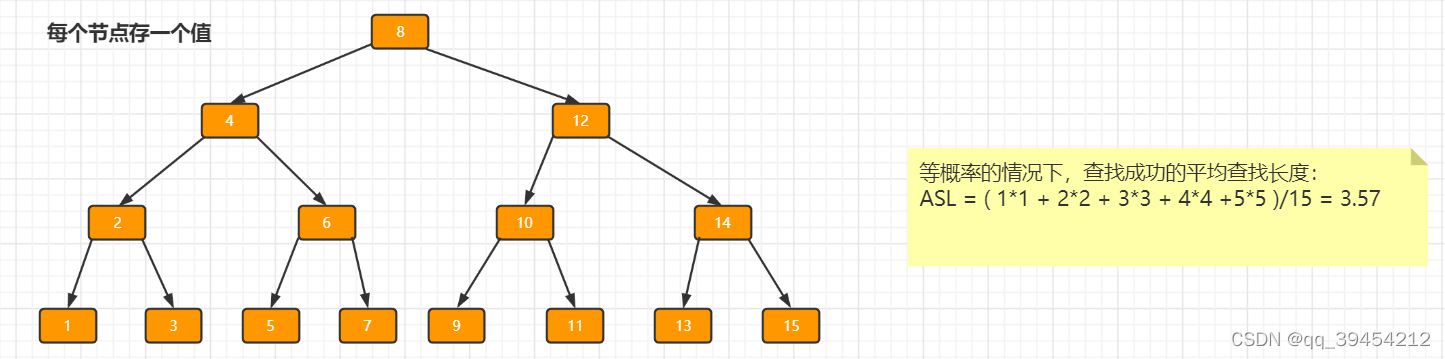
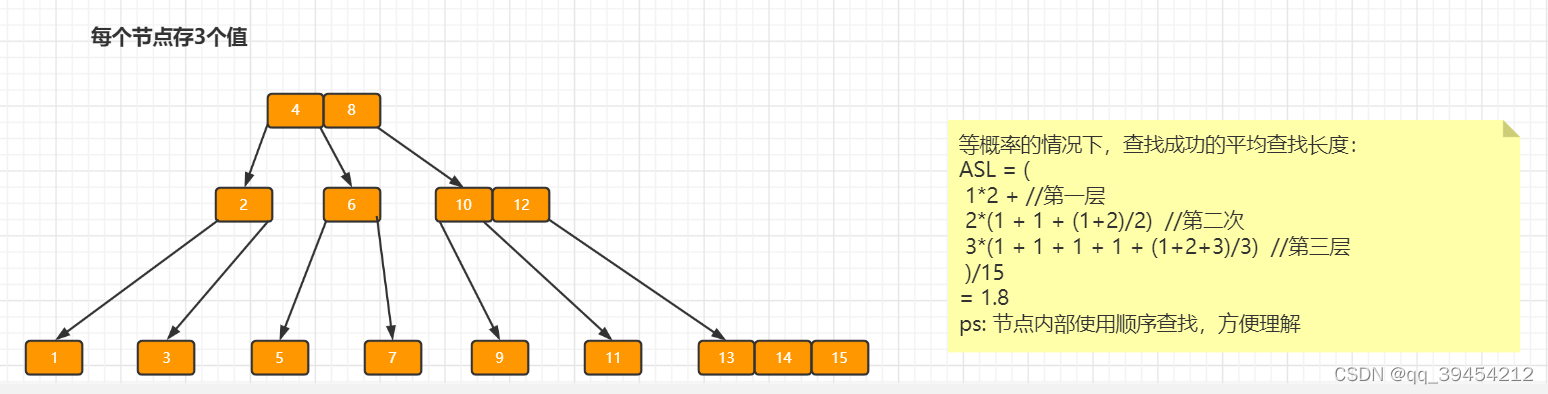
?从查找成功的平均查找长度入手,明显每个结点存储的结点多的,查找长度较小。
2.定义
?B树(也称B-树),它是一颗多路平衡查找树。我们描述一颗B树时需要指定它的阶数,阶数表示了一个结点最多有多少个孩子结点,一般用字母m表示阶数。当m取2时,就是我们常见的二叉搜索树。
?一颗m阶的B树定义如下:
(看了很多资料,一会关键字个数,一会子节点个数,我这里统一一下,就用关键字了,反正“关键字个数”=“子节点个数”- 1)
?1)非根结点至少有?m/2?-1个关键字(?1.5?为1.5向上取整=2),最多有m-1个关键字。
?2)根结点最少可以只有1个关键字,最多有m-1个关键字。
?3)每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
?4)所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同。
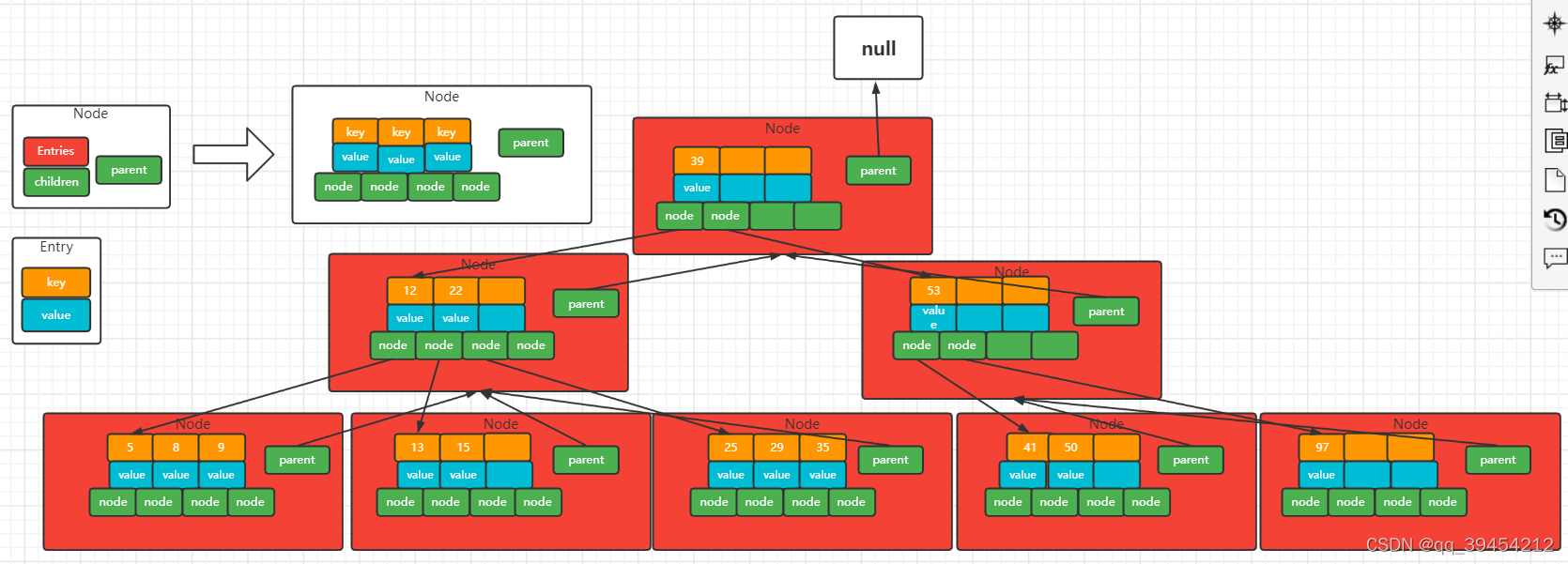
?上图是一颗阶数为4的B树。在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小。每个结点中存储了关键字(key)和关键字对应的数据(value),孩子结点的指针和父节点。我们将一个key和其对应的value称为一个记录Entry。但为了方便描述,除非特别说明,后续文中就用key来代替((key, value), children,parent)。
3.操作
?1)插入
插入操作是指插入一条记录,即(key, value)的键值对。如果B树中已存在需要插入的键值对,则直接返回。若B树不存在这个key,则一定是在叶子结点中进行插入操作。
?(1)根据要插入的key的值,找到叶子结点并插入。
?(2)判断当前结点key的个数是否小于等于m-1,若满足则结束,否则进行第3步。
?(3)以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将左右结点结点指向父结点,继续进行第3步。
?ps:满足B树定义的情况下,key个数的最大值为maxKeySize,key个数的最小值为maxKeySize
?key插入后,如果节点中key的个数大于maxKeySize,分裂详细步骤如下:
?分裂节点为Right,分裂节点的中间key为midKey,分裂节点左半部分的key为leftKeys,分裂节点在父节点中的位置为index
?若存在父节点则为Parent。
?若分裂的节点非叶子节点,分裂节点左半部分的children为leftChilden。
-
Right为叶子结点
- Right存在父结点,新建一个结点Left,将leftKeys插入到Left的Entries中,在Parent的children中的index位置插入新结点Left,新结点Left的parent指向Parent,Right的Entries中LeftKeys和mid需要删除
- Right不存在父结点,新建一个结点Left,将leftKeys插入到Left的Entries中,新建一个父结点Parent,将midKey插入到Parent的Entries中,Right的Entries中LeftKeys和mid需要删除,再将Left和Right插入到Parent的children中,新结点Left的parent和Right的parent指向Parent
-
Right为非叶子结点
- Right存在父结点,新建一个结点Left,将leftKeys插入到Left的Entries中,leftChilden插入到Left的children中,在Parent的children中的index位置插入新结点Left,新结点Left的parent指向父结点, Right的Entries中LeftKeys和mid需要删除,Right的children中的leftChilden需要删除
- Right不存在父结点,新建一个结点Left,将leftKeys插入到Left的Entries中, leftChilden插入到Left的children中,新建一个父结点Parent,将midKey插入到父结点中,Left和Right插入到Parent的children中,Left和Right指向父结点,Right的Entries中LeftKeys和mid需要删除,Right的children中的leftChilden需要删除
下面以5阶B树为例,介绍B树的插入操作,在5阶B树中,结点最多有4个key,最少有2个key
新建一棵树,树中存在一个节点,即root节点,root节点中此时是没有key的

a)在空树中插入39

此时根结点就一个key,此时根结点也是叶子结点;
ps:下面没有插入的key的结点,就不画了。
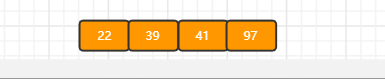
根结点此时有4个key
c)继续插入53
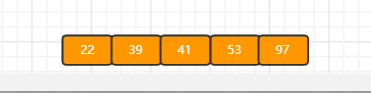
?插入后超过了最大允许的关键字个数4,所以以key值为41为中心进行分裂(分裂规则是最大允许的关键字个数/2,不用向上取整,所以这里是4/2=2,下标从0开始,选取下标为2的key,即41),结果如下图所示,首先新建一个节点Left,将midKey左边的key给Left,再新建一个节点newRoot,midKey给newRoot,newRoot分别再指向这两个节点,这两个节点的parent再指向newRoot,B树的root指向newRoot,此时满足B树条件,插入操作结束。
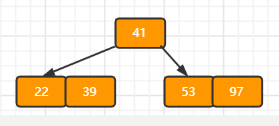
d)依次插入13,21,40,同样会造成分裂,结果如下图所示。操作过程是首先新建一个节点Left,将midKey左边的key给Left,midKey插入父节点,父节点的children头插Left,Left的parent指向原本的父节点,此时满足B树条件,插入操作结束。
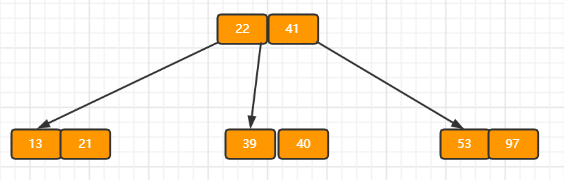
e)依次插入30,27, 33 ;36,35,34 ,24,29,结果如下图所示。
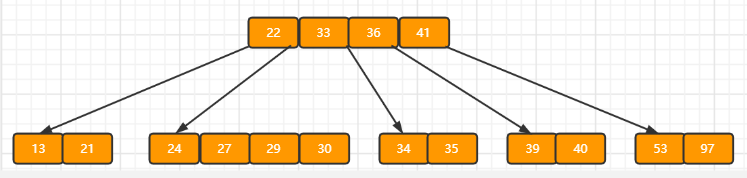
f)插入key值为26的记录,插入后的结果如下图所示。此时不满足B树定义了。
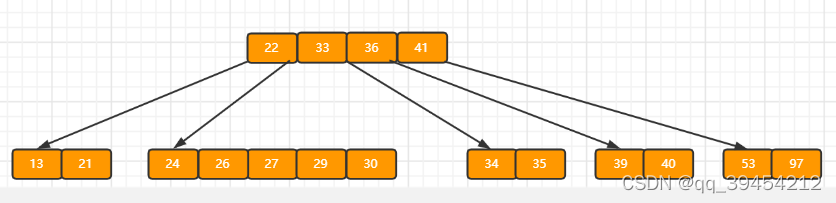
当前结点需要以27为中心分裂,并向父结点进位27,然后当前结点指向父结点,结果如下图所示。
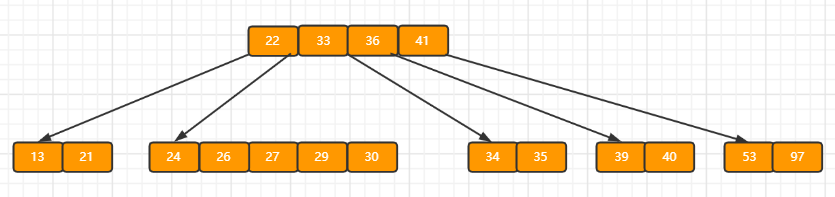
进位后导致当前结点(即根结点)也需要分裂,分裂的结果如下图所示。
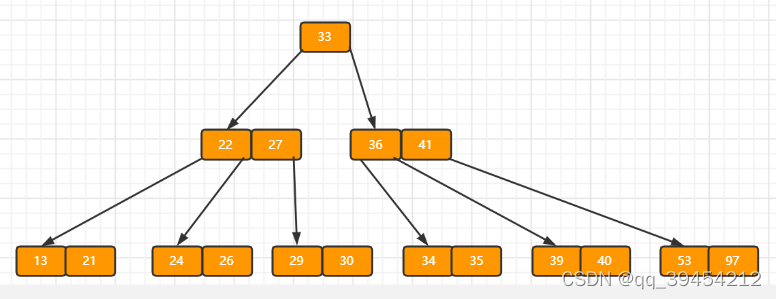
分裂后当前结点指向新的根,此时无需调整。
g)最后再依次插入key为17,28,29,31,32的记录,结果如下图所示。
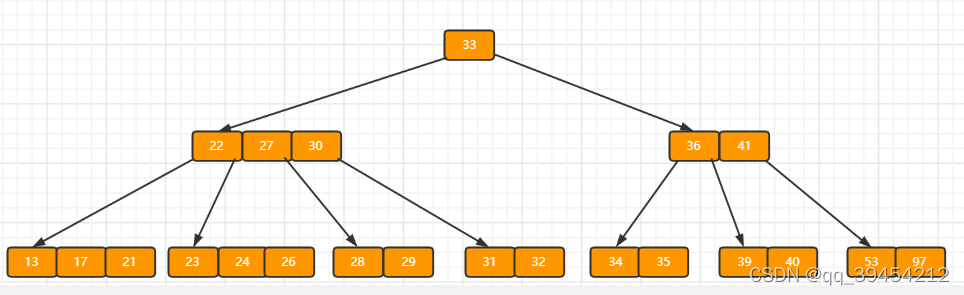
? 一般来说,对于确定的m和确定类型的记录,结点大小是固定的,无论它实际存储了多少个记录。但是分配固定结点大小的方法会存在浪费的情况,比如key为28,29所在的结点,还有2个key的位置没有使用,但是已经不可能继续在插入任何值了,因为这个结点的前序key是27,后继key是30,所有整数值都用完了。所以如果记录先按key的大小排好序,再插入到B树中,结点的使用率就会很低,最差情况下使用率仅为50%。
?2)删除
删除操作是指,根据key删除记录,如果B树中的记录中不存对应key的记录,则直接返回。
?(1)如果当前需要删除的key位于非叶子结点上,则用后继key(这里的后继key均指后继记录的意思)覆盖要删除的key,然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上,这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步。
?(2)该结点key个数大于等于?m/2?-1,结束删除操作,否则执行第3步。
?(3)如果兄弟结点key个数大于?m/2?-1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。如果key个数等于?m/2?-1,将父结点中的key下移与当前结点及它的兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
?有些结点它可能即有左兄弟,又有右兄弟,那么我们任意选择一个兄弟结点进行操作即可(我这里选择左兄弟)。如果只有右兄弟,那就选择右兄弟,只有左兄弟那就选择左兄弟
?删除key的节点为node,node的key的个数为keySize,node的key的个数为keySize,node的在父节点中的位置为index,node的左兄弟节点为Left,右兄弟节点为Right
?若存在父节点则为Parent
?key删除后,node中keySize小于minKeySize,则需要合并,详细步骤如下:
- node为叶子节点
- 兄弟够借(兄弟节点的keySize大于minKeySize)
- 如果index=0,说明只能找Right借,Parent中index处的entry下移到node的entries的最后一位,Right中第一个entry上移,Right第一个entry需要删除,此时满足B树条件。
- 如果index>0,说明此时能找Left借,Parent中index-1处的entry下移到node的entries的第一位,Left中最后一个entry上移,Left最后一个entry需要删除,此时满足B树条件。
- 兄弟不够借(兄弟节点的keySize等于minKeySize)
- 如果index=0,Parent的index处的entry下移到Right的entries的第一个,Left中的entry再加入到Right中;Parent的entries的index处的entry删除,Parent的children的index处的元素删除;node的parent置空。
- 如果index>0,Parent的index-1处entry下移到Left的entries的最后一个,node的entry再加入到Left中;Parent的entries的index-1处的entry删除,Parent的children的index处的元素删除;node的parent置空。
- 兄弟够借(兄弟节点的keySize大于minKeySize)
- node不为叶子节点
- 兄弟够借(兄弟节点的keySize大于minKeySize)
- 如果index=0,说明只能找Right借,Parent中index处的entry下移到node的entries的最后一位,Right中第一个entry上移,Right的children的第一个Node加入node的children中,Right中第一个entry删除,Right的children的第一个Node的parent更改指向Left
- 如果index>0,说明此时能找Left借,Parent中index+1处的entry下移到node的entries的第一位,Left的最后一个entry上移,Left的children的最后一个Node加入node的children中,Left的最后一个entry删除,Left的children的最后一个Node的parent更改指向Right
- 兄弟不够借(兄弟节点的keySize等于minKeySize)
- 如果index=0,Parent的index处的entry下移到Right的entries的第一个,node中的entry再加入到Right中;Left的children全部插入到Right的children中,Left的childrent的元素的的parent全部指向Right,Parent的entries的index处的entry删除,Parent的children的index处的元素删除;node的parent置空。
- 如果index>0,Parent的index-1处entry下移到Left的entries的最后一个,node的entry再加入到Left中;Right的children全部插入到Left的children中,Right的childrent的元素的parent指向Left,Parent的entries的index-1处的entry删除,Parent的children的index处的元素删除;node的parent置空。
- 兄弟够借(兄弟节点的keySize大于minKeySize)
?下面以5阶B树为例,介绍B树的删除操作,5阶B树中,结点最多有4个key,最少有2个key
a)原始状态
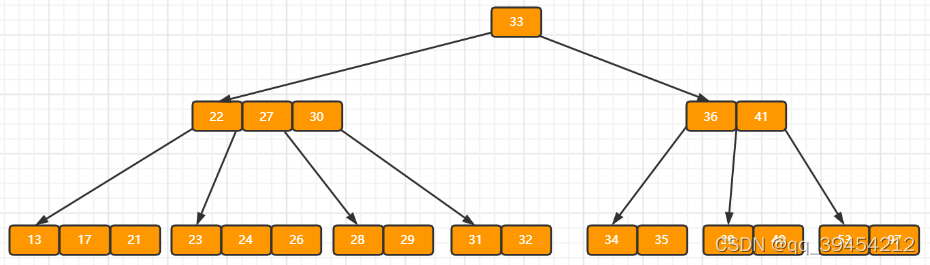
b)在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束。
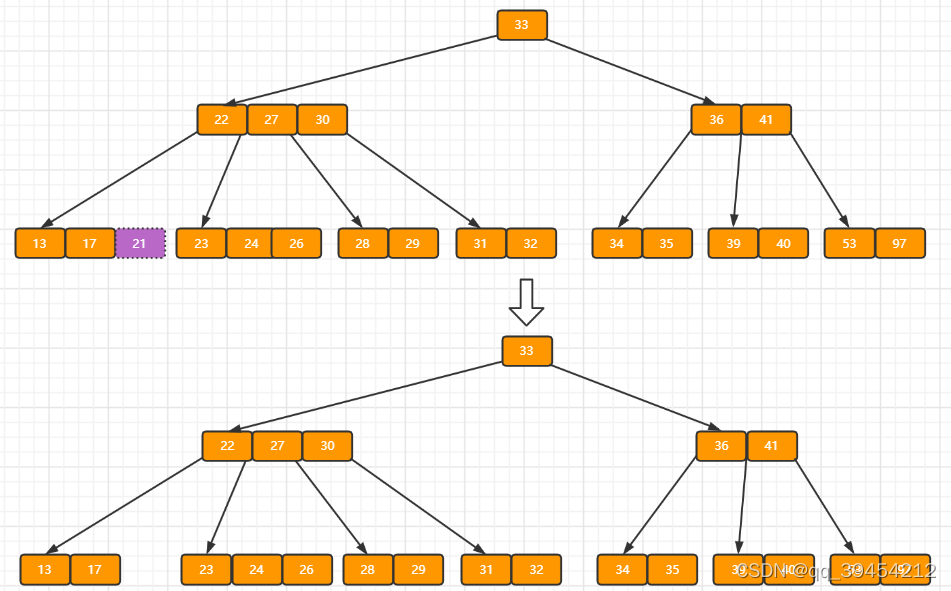
c)在上述情况下接着删除27。从上图可知27位于非叶子结点中,所以用27的后继替换它。从图中可以看出,27的后继为28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示。
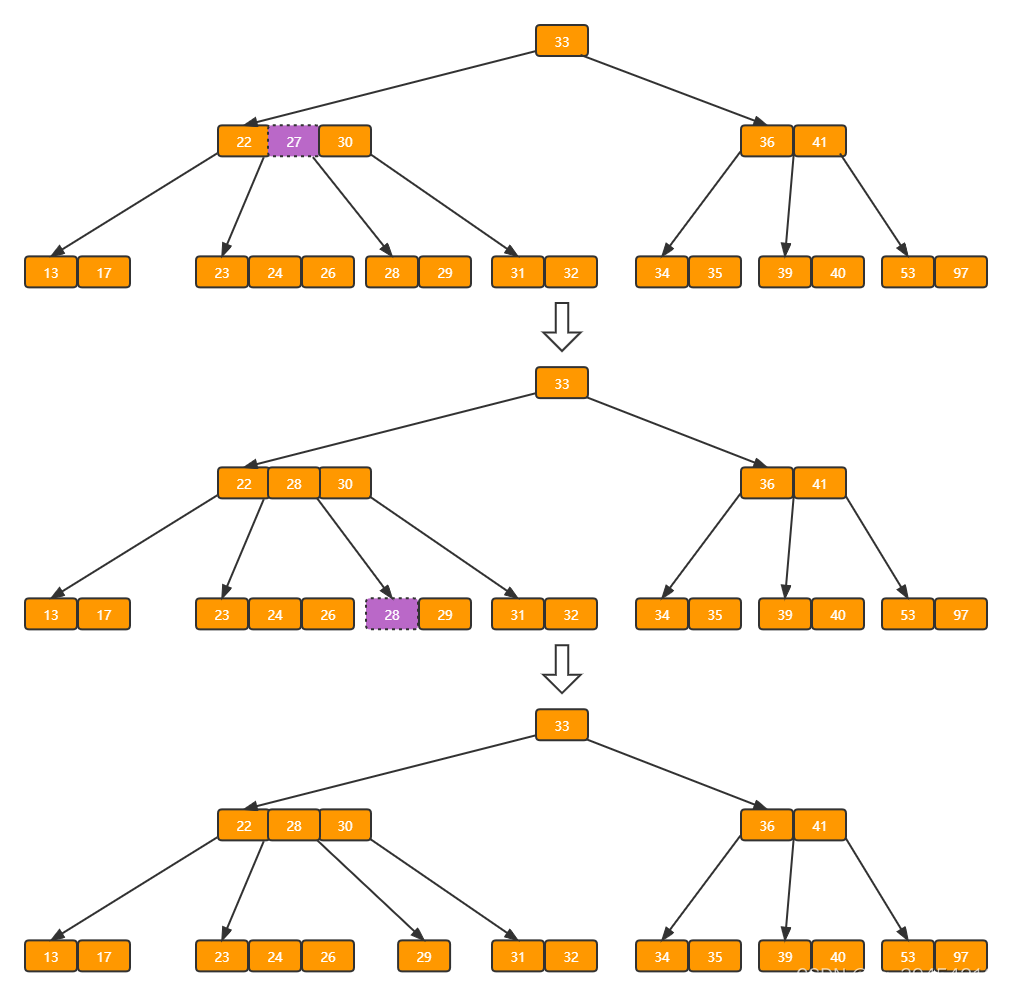
?删除后发现,当前叶子结点的记录的个数小于2,而它的兄弟结点中有3个记录(当前结点还有一个右兄弟,选择右兄弟就会出现合并结点的情况,不论选哪一个都行,只是最后B树的形态会不一样而已),我们可以从兄弟结点中借取一个key。所以父结点中的28下移,兄弟结点中的26上移,删除结束。结果如下图所示。
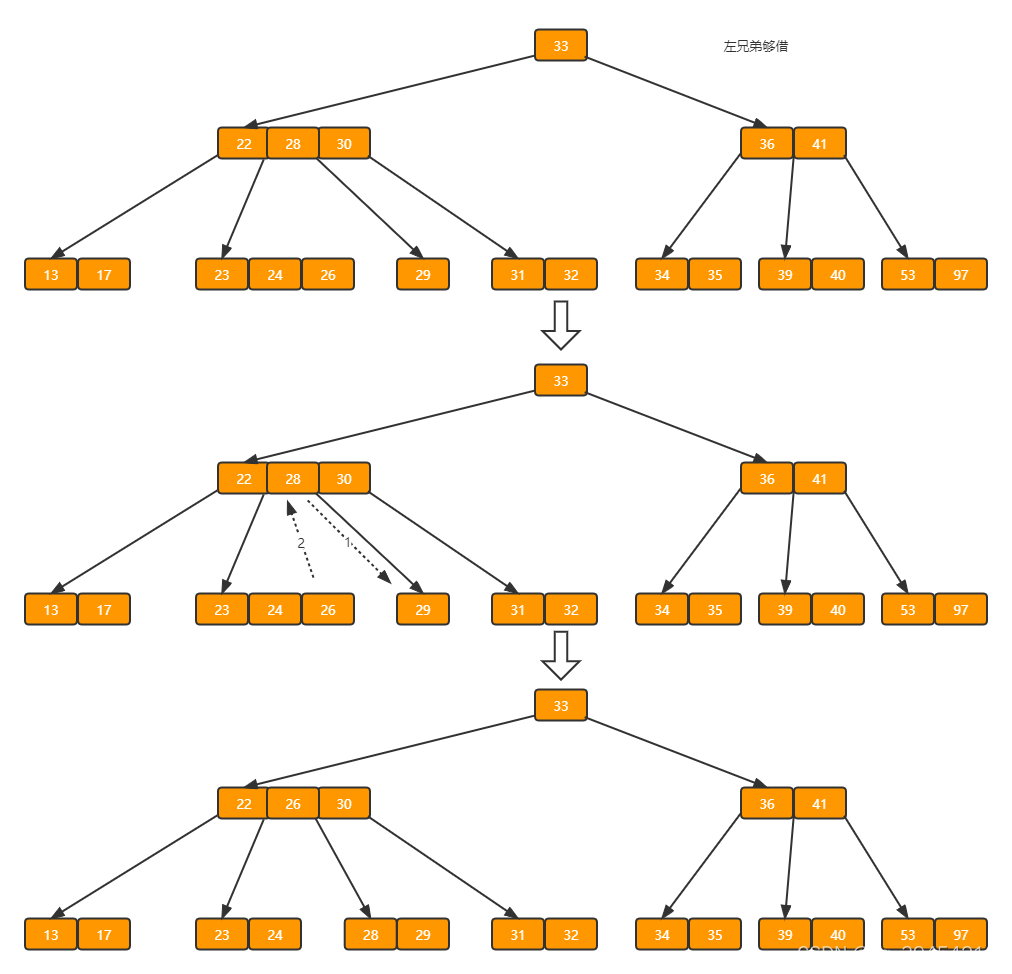
d)在上述情况下接着删除32,结果如下图。
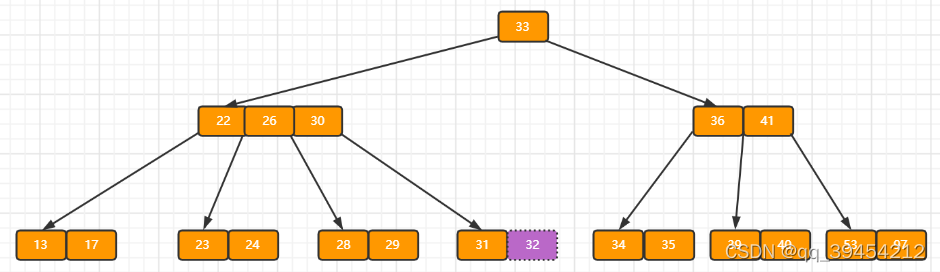
?当删除后,当前结点中只有一个key,而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并,成为一个新的结点,当前结点的指针指向父结点。结果如下图所示。(看到这里应该明白了,只要删除key的节点的父节点的key的数量没有发生变化,就不会出现树的高度下降)
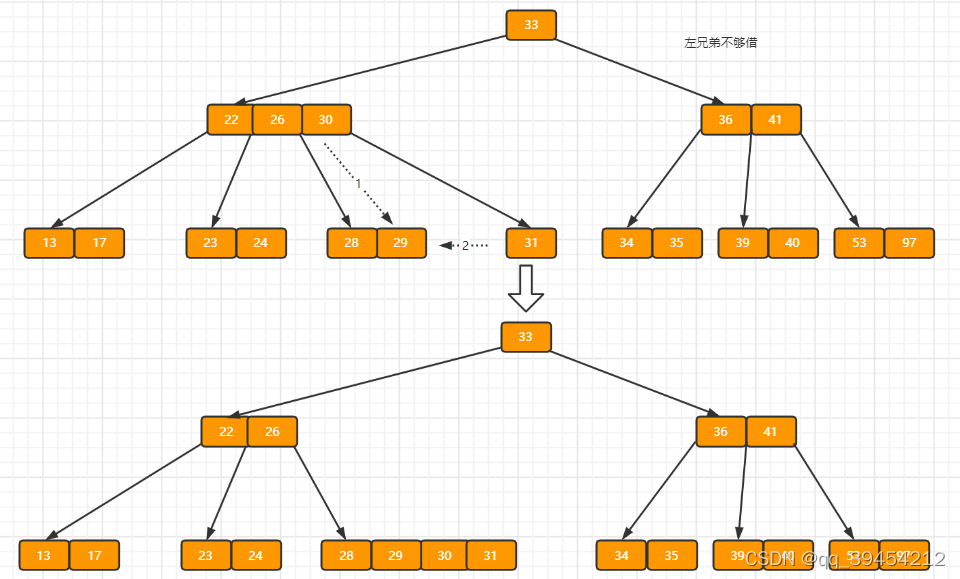
?当前结点key的个数满足条件,故删除结束。
e)上述情况下,我们接着删除key为40的记录,删除后结果如下图所示。
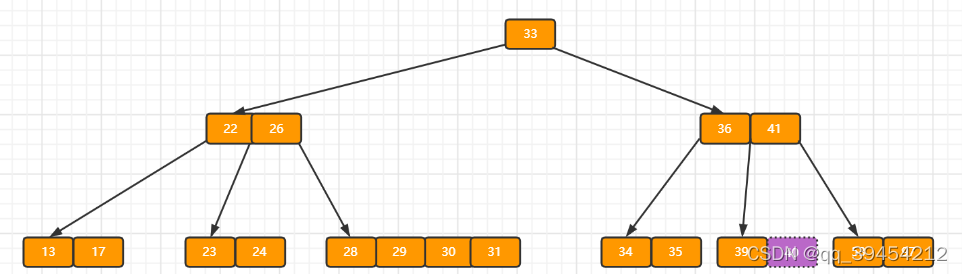
?同理,当前结点的记录数小于2,兄弟结点中没有多余key,所以父结点中的key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)结点合并,合并后的指向当前结点的指针就指向了父结点。
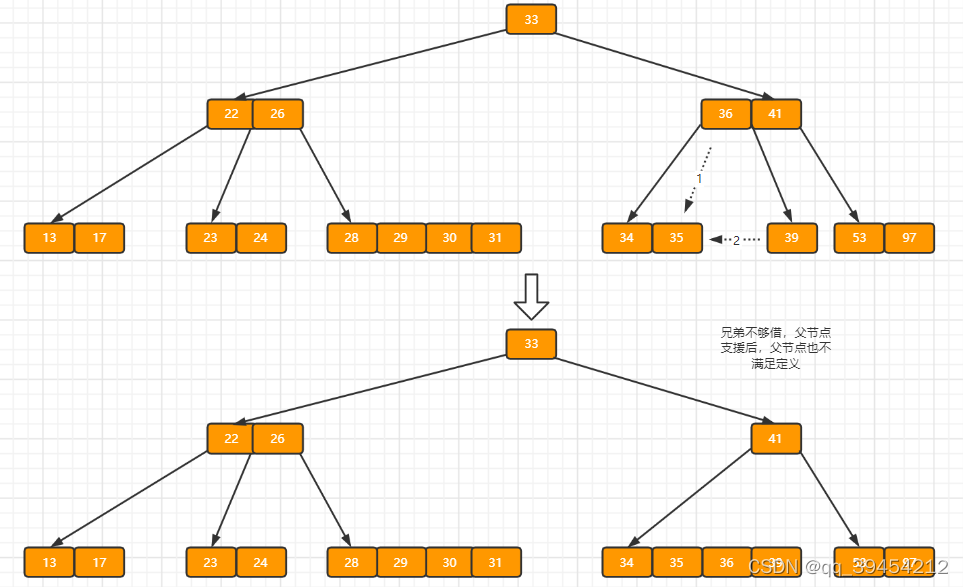
?同理,对于当前结点而言只能继续合并了,最后结果如下所示。
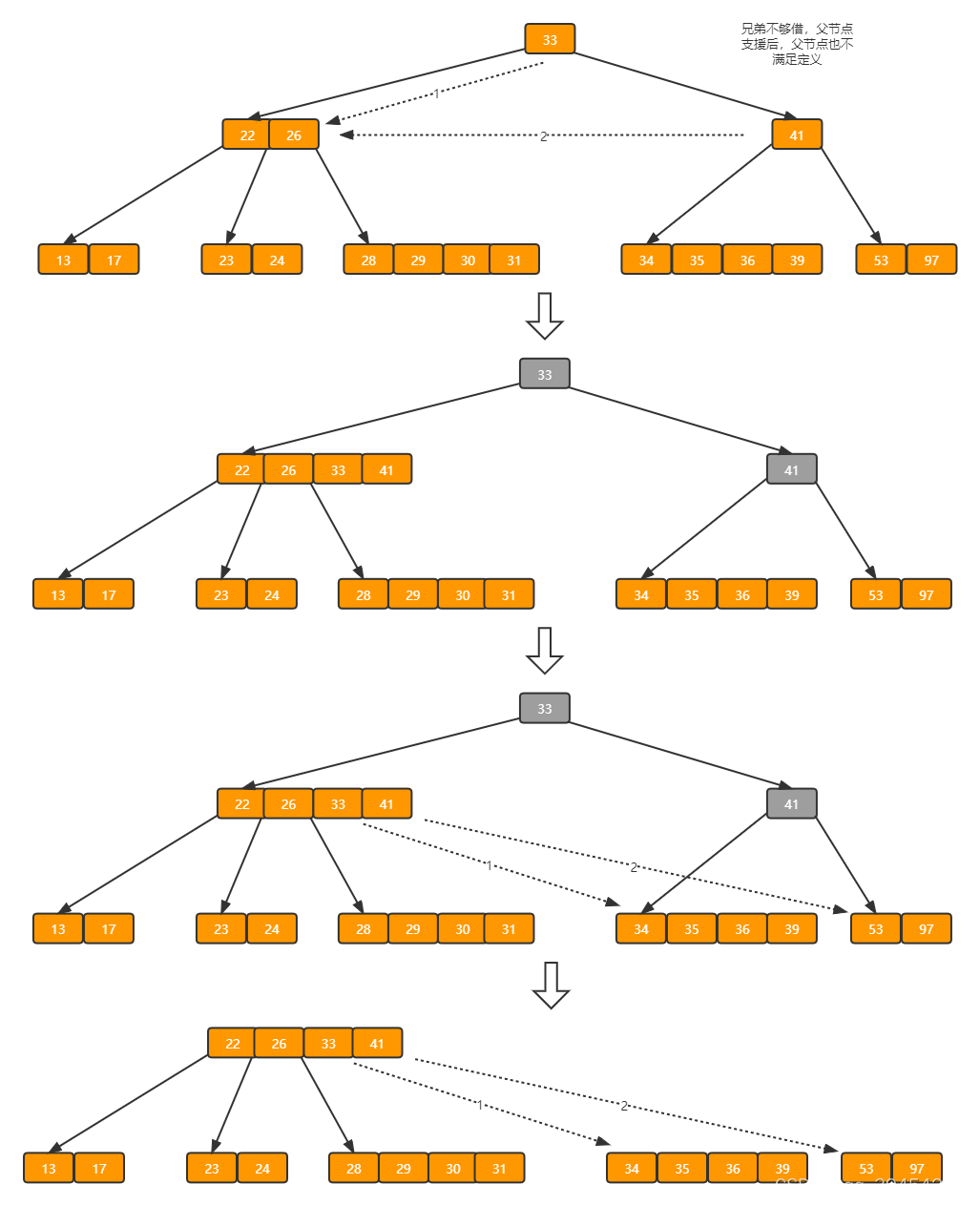
?合并后结点当前结点满足条件,删除结束。
ps:承接e)步骤,如果B树是这样呢?
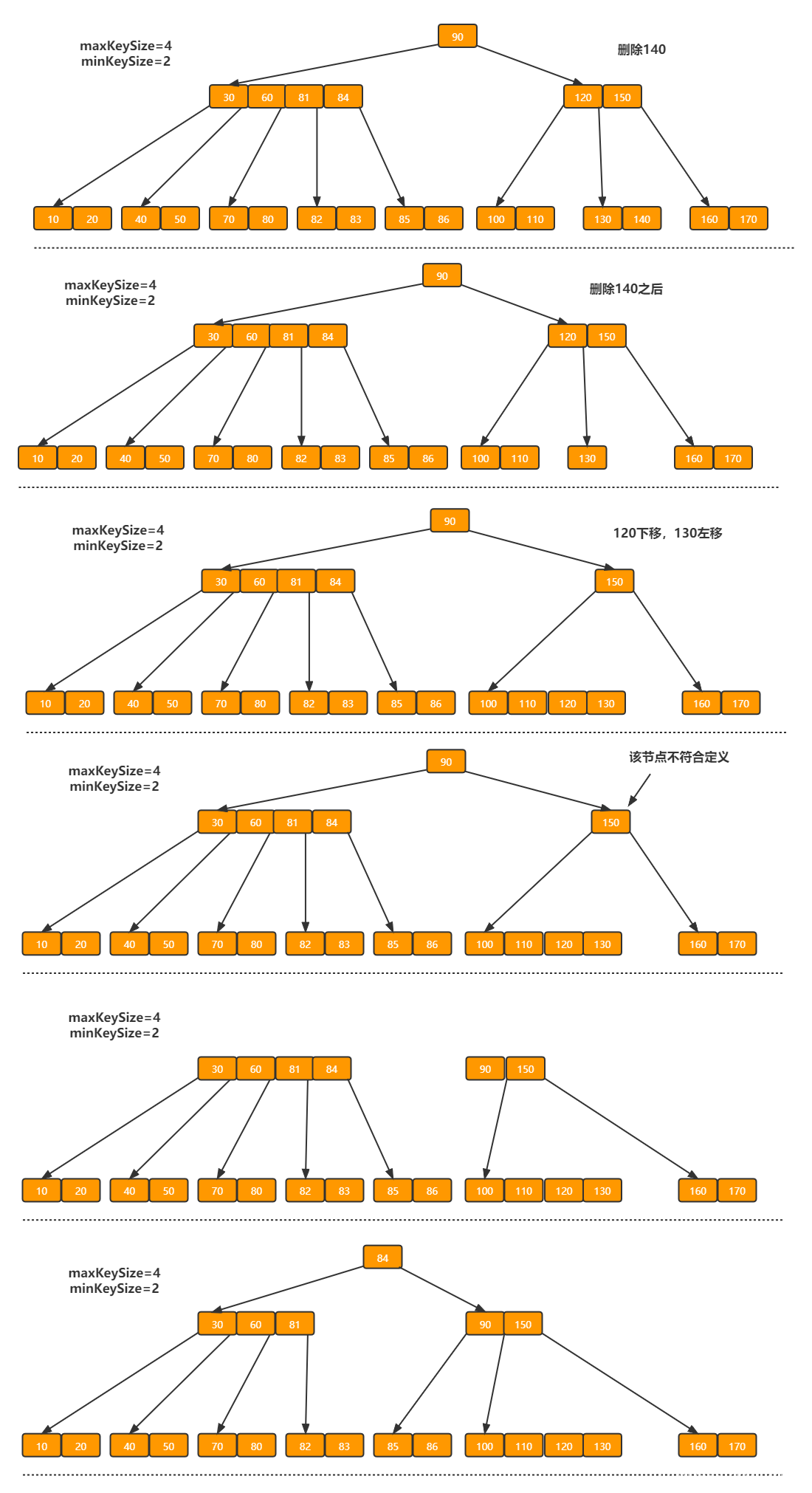
4.代码
1)Entry
public class Entry<K, V> {
private K key;
private V value;
public void setKey(K key) {
this.key = key;
}
public K getKey() {
return this.key;
}
public void setValue(V value) {
this.value = value;
}
public V getValue() {
return this.value;
}
public Entry(K key, V value) {
this.key = key;
this.value = value;
}
public Entry() {
}
@Override
public String toString() {
return "key: " + this.key;
}
}
2)SearchResult
public class SearchResult<K, V> {
private boolean isExist;
private int index;
private Node<K, V> node;
public SearchResult(boolean isExist, int index, Node<K, V> node) {
this.isExist = isExist;
this.index = index;
this.node = node;
}
public boolean isExist() {
return isExist;
}
public V getValue() {
if (node != null) {
return (V) node.getEntries().get(index);
} else {
return null;
}
}
public int getIndex() {
return index;
}
public Node<K, V> getNode() { return node; }
}
3)
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
public class Node<K,V> {
private Node(List<Entry<K, V>> entries, List<Node<K, V>> children, boolean leaf, Comparator<K> kComparator, Node<K, V> parent) {
this.entries = entries;
this.children = children;
this.leaf = leaf;
this.kComparator = kComparator;
this.parent = parent;
}
//关键字列表
private List<Entry<K,V>> entries;
//子结点列表
private List<Node<K, V>> children;
//是否为叶子节点
private boolean leaf;
//键值比较函数对象,如果采用倒序或者其它排序方式,传入该对象
private Comparator<K> kComparator;
private Node<K, V> parent;
public Node<K, V> getParent() {
return parent;
}
public void setParent(Node<K, V> parent) {
this.parent = parent;
}
//判断node的entries的数量是否超过最大keyMaxSize
public boolean isOverFlow(int keyMaxSize) {
return this.entries.size() > keyMaxSize;
}
//比较两个key,如果没有传入自定义排序方式则采用默认的升序
public int compare(K key1, K key2) {
return this.kComparator == null ? ((Comparable<K>) key1).compareTo(key2) : kComparator.compare(key1, key2);
}
Node(int degree) {
this.entries = new ArrayList<Entry<K, V>>(degree);
this.children = new ArrayList<Node<K, V>>(degree);
this.leaf = false;
this.parent = null;
}
public int nodeSize() {
return this.entries.size();
}
public List<Entry<K, V>> getEntries() {
return entries;
}
public List<Node<K, V>> getChildren() {
return children;
}
public boolean isLeaf() {
return leaf;
}
public void setLeaf(boolean leaf) {
this.leaf = leaf;
}
public Comparator<K> getkComparator() {
return kComparator;
}
public void setkComparator(Comparator<K> kComparator) {
this.kComparator = kComparator;
}
public SearchResult<K, V> search(K key){
int left = 0; //左指针
int right = this.getEntries().size()-1;//右指针
V res = null;//返回值
int mid = (left+right)/2;//中间的位置
boolean isExist = false; //判断是否找到了
int index = 0; //要找的关键字的下标
while(left <= right){
mid = (left+right)/2;//中间的位置
Entry<K,V> midEntry = this.entries.get(mid);//拿到中间的关键字
int comparator = this.compare(key,midEntry.getKey());
if(comparator == 0){//找到了
isExist = true;
index = mid;
res = this.entries.get(mid).getValue();
break;
}else if(comparator==1){//在右侧
left = mid + 1;
}else{//midKey大于key 在左侧
right = mid - 1;
}
}
//二分查找结束了
//B树首次插入节点,会出现left = 0且right = -1的情况
if(isExist == false) {
if (right == -1) {
index = left;
} else {
//能走到这里说明left > right
//选择较小的哪个值
int min = Math.min(left, right);
K midKey = this.entries.get(min).getKey();//虽然没有找到key但是找到了离key最近的一个关键字
int comRe = compare(key, midKey); //判断key和关键字哪个大
if(comRe>0){ //key大 那么就是关键字的右子树
index = min + 1;
}else { //key小 返回当前left的左子树
index = min ;
}
}
}
return new SearchResult<K, V>(isExist, index, res == null ? null : this);
}
//得到index处的项
public Entry<K, V> entryAt(int index) {
return this.entries.get(index);
}
private void insertEntry(Entry<K, V> entry, int index) {
this.entries.add(index, entry);
}
//将新关键字插入 如果存在相同的关键字key不允许插入
public boolean insertEntry(Entry<K,V> entry){
SearchResult<K, V> result = search(entry.getKey()); //这里会返回适合的节点
if (result.isExist()) { //如果有了相同的key就不然插入
return false;
} else {
insertEntry(entry, result.getIndex());
return true;
}
}
public Node<K, V> childAt(int index) {
return this.children.get(index);
}
}
4)BTree
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class BTree<K, V> {
//默认是5阶树,度为5
private static int DEFAULT_DEGREE = 100;
//根节点
private Node<K, V> root;
private int m;
//非根节点的最小项数,体现的是除了根节点,其余节点都是分裂而来的!
//节点的最大儿子数
private int nodeMaxSize;
//节点的最大关键字数
private int keyMaxSize;
//这里体现了除根节点和叶子节点外每个节点的最小儿子数量
private int nodeMinSize;
//节点的最小关键字数
private int keyMinSize;
//比较函数对象
private Comparator<K> kComparator;
public BTree() {
this(DEFAULT_DEGREE);
this.m = DEFAULT_DEGREE;
}
public BTree(int degree) {
if (degree < 3) {
throw new RuntimeException("degree less than 3!!");
}
this.m = degree;
this.nodeMaxSize = this.m;
this.keyMaxSize = this.m - 1;
this.nodeMinSize = upToInt(this.m ,2);
this.keyMinSize = upToInt(this.m ,2) - 1;
this.root = new Node<>(this.keyMaxSize);
root.setLeaf(true);
}
private int upToInt(int dividend,int divisor) {
return dividend % 2 == 1 ? (dividend + 1) / divisor : dividend / divisor;
}
private int getKeyMaxSize() {
return keyMaxSize;
}
public SearchResult<K, V> searchfromRoot (K key){
return search(this.root, key);
}
private SearchResult<K, V> search(Node<K, V> node, K key) {//从查找根节点
SearchResult<K, V> re = node.search(key);
if (re.isExist()) {
return re;
} else {
//回归条件
if (node.isLeaf()) {//找到了叶子节点也没找到就不需要继续寻找下去了
return new SearchResult<>(false, re.getIndex(), node);
}
int index = re.getIndex();
//递归搜索子节点
return search(node.childAt(index), key);
}
}
private void insertNode(Node<K, V> node, int index, Entry<K, V> entry) {
//entries插入之后,再判断是否超过最大值
node.getEntries().add(index, entry);
Entry<K, V> midEntry = null;
if(!isGreaterThanKeyMaxSize(node)) {//没有超过,则结束
return;
} else {
int midIndex = this.keyMaxSize / 2;
midEntry = node.getEntries().get(midIndex);
//新建一个newNode分裂的key左边的key加入新节点,将相同数量的children的元素也加入到新节点中,原来节点中的删除
Node<K, V> newNode = new Node<>(this.keyMaxSize);
for (int i = 0;i < midIndex+1; i++) {
newNode.getEntries().add(node.getEntries().get(0));
node.getEntries().remove(0);
}
newNode.getEntries().remove(midIndex);
if (!node.isLeaf()) { // 非叶子节点
for (int i = 0;i < midIndex+1; i++) {
newNode.getChildren().add(node.getChildren().get(0));
node.getChildren().get(0).setParent(newNode);
node.getChildren().remove(0);
}
}
if (newNode.getChildren().size() == 0) {
newNode.setLeaf(true);
}
Node<K, V> parent = node.getParent();
if(parent != null) {//判断是否有父节点
newNode.setParent(parent);
for (int i = 0; i < parent.getChildren().size(); i++) {
if (node == parent.getChildren().get(i)) {
index = i;
break;
}
}
parent.getChildren().add(index, newNode);
insertNode(parent, index, midEntry);
} else { //没有父节点
Node<K, V> newRoot = new Node<>(this.keyMaxSize);
newRoot.getEntries().add(midEntry);
List<Node<K, V>> rootChildren = newRoot.getChildren();
rootChildren.add(newNode);
newNode.setParent(newRoot);
rootChildren.add(node);
node.setParent(newRoot);
if (node.getChildren().size() == 0) {
node.setLeaf(true);
}
this.root = newRoot;
return;
}
}
}
private boolean isGreaterThanKeyMaxSize(Node<K, V> node) {
return node.isOverFlow(this.getKeyMaxSize());
}
public void insert(Entry<K, V> entry) {
SearchResult<K, V> sr = searchfromRoot(entry.getKey());
if (sr.isExist()) {
return;
}
insertNode(sr.getNode(), sr.getIndex(), entry);//sr.getIndex()表示应该往叶子节点的插的index
}
public void output() {
Queue<Node<K, V>> queue = new LinkedList<Node<K, V>>();
queue.offer(this.root);
while (!queue.isEmpty()) {
Node<K, V> node = queue.poll();
for (int i = 0; i < node.nodeSize(); ++i) {
System.out.print(node.entryAt(i) + " ");
if (i == node.nodeSize() - 1) {
System.out.print(" node: "+node + " parent: " +node.getParent());
}
}
System.out.println();
if (!node.isLeaf()) {
for (int i = 0; i <= node.getChildren().size() - 1; ++i) {
queue.offer(node.childAt(i));
}
}
}
}
private boolean isExists(Entry<K, V> entry) {
return searchfromRoot(entry.getKey()).isExist();
}
private SearchResult<K, V> prefixNode(Entry<K, V> entry){
SearchResult<K, V> sr = searchfromRoot(entry.getKey());
Node<K, V> node = sr.getNode();
int index = sr.getIndex();
Node<K, V> preNode = node.getChildren().get(index);
while (!preNode.isLeaf()) {
List<Node<K, V>> children = preNode.getChildren();
preNode = children.get(children.size()-1);
}
return new SearchResult<K, V>(true, preNode.getEntries().size()-1, preNode);
}
private SearchResult<K, V> suffixNode(SearchResult<K, V> sr){
Node<K, V> node = sr.getNode();
int index = sr.getIndex();
Node<K, V> sufNode = node.getChildren().get(index + 1);
while (!sufNode.isLeaf()) {
List<Node<K, V>> children = sufNode.getChildren();
sufNode = children.get(0);
}
return new SearchResult<K, V>(true, 0, sufNode);
}
public void delete(Entry<K, V> entry) {
SearchResult<K, V> res = searchfromRoot(entry.getKey());
if (!res.isExist()) {
return;
}
Node<K, V> node = res.getNode();
int index = res.getIndex();
if (!node.isLeaf()) {
//如果不是叶子节点,则找到后继节点中的后继Entry
SearchResult<K, V> sufNodeSR = suffixNode(res);
Node<K, V> sufNode = sufNodeSR.getNode();
int sufIndex = sufNodeSR.getIndex();
Entry<K, V> sufEntry = sufNode.getEntries().get(sufIndex);
res.getNode().getEntries().set(index, sufEntry);
deleteLeafNodeEntry(sufNode, sufIndex);
} else {
//如果是叶子节点,则直接删除
deleteLeafNodeEntry(node, index);
}
}
private void deleteLeafNodeEntry(Node<K, V> node, int index) {
int entriesSize = node.getEntries().size();
if (entriesSize > this.keyMinSize) {
//本节点中minKeySize < keySize < maxKeySize
node.getEntries().remove(index);
return;
} else {
//entriesSize == this.keyMinSize,B树在构建的过程中,不可能出现entriesSize < this.keyMinSize的情况
//首先把该Entry删除
node.getEntries().remove(index);
if (node == this.root) {
return;
}
int parentEntrisSize = -1;
Node<K, V> parentNode = node;
do {
parentNode = nodeLessThanKeyMinSize(parentNode, index);
parentEntrisSize = parentNode.getEntries().size();
}while (parentNode != this.root && parentEntrisSize < this.keyMinSize);
}
}
private Node<K, V> nodeLessThanKeyMinSize(Node<K, V> node, int index) {
Node<K, V> parent = node.getParent();
List<Node<K, V>> parentChildren = parent.getChildren();
int nodeIndex = -1;
for (int i = 0; i < parentChildren.size(); i++) {
if (node == parentChildren.get(i)) {
nodeIndex = i;
break;
}
}
Node<K, V> leftNode = null;
Node<K, V> rightNode = null;
boolean isRotate = false;
if (nodeIndex > 0 && nodeIndex < parentChildren.size() - 1) {
leftNode = parentChildren.get(nodeIndex - 1);
if (isRotate == false && leftNode.getEntries().size() > this.keyMinSize) {
//左兄弟够借,需要右旋
rightRotate(node, nodeIndex);
isRotate = true;
}
rightNode = parentChildren.get(nodeIndex + 1);
if (isRotate == false && rightNode.getEntries().size() > this.keyMinSize) {
//右兄弟够借,需要左旋
leftRotate(node, nodeIndex);
isRotate = true;
}
} else if (nodeIndex == 0){
rightNode = parentChildren.get(nodeIndex + 1);
if (rightNode.getEntries().size() > this.keyMinSize) {
//右兄弟够借,需要左旋
leftRotate(node, nodeIndex);
isRotate = true;
}
} else {
leftNode = parentChildren.get(nodeIndex - 1);
if (leftNode.getEntries().size() > this.keyMinSize) {
//左兄弟够借,需要右旋
rightRotate(node, nodeIndex);
isRotate = true;
}
}
//判断是否发生了旋转,如果isRotate=true,说明发生了旋转,B树就平衡了,无需进行下面的操作了
if (isRotate == false) {
//若没有发生旋转,所以B树现在还没有平衡
if (nodeIndex > 0) {
//entry进入左兄弟
if (parent == this.root && parent.getEntries().size() == 1) {
Node<K, V> rootLeftChild = parent.getChildren().get(nodeIndex - 1);
rootLeftChild.getEntries().add(parent.getEntries().get(0));
for (int i = 0; i < node.getEntries().size(); i ++) {
rootLeftChild.getEntries().add(node.getEntries().get(i));
}
if (!node.isLeaf()) {
for (int i = 0; i < node.getChildren().size(); i ++) {
rootLeftChild.getChildren().add(node.getChildren().get(i));
node.getChildren().get(i).setParent(rootLeftChild);
}
}
//以下操作,方便虚拟机回收
//node和root的关系
this.root.getChildren().remove(1);
node.setParent(null);
//node和子节点的关系
for (Node<K, V> kvNode : node.getChildren()) {
kvNode.setParent(rootLeftChild);
}
node.getChildren().clear();
//right和root的关系
this.root.getChildren().clear();
this.root = rootLeftChild;
rootLeftChild.setParent(null);
return this.root;
} else {
//进入左兄弟节点
if (node.isLeaf()) {
Entry<K, V> parentEntry = parent.getEntries().get(nodeIndex - 1);
leftNode.getEntries().add(parentEntry);
for (int i = 0; i < node.getEntries().size(); i++) {
leftNode.getEntries().add(node.getEntries().get(i));
}
//node删除,父节点的children处理
node.setParent(null);
parent.getChildren().remove(nodeIndex);
parent.getEntries().remove(nodeIndex - 1);
} else {
Entry<K, V> parentEntry = parent.getEntries().get(nodeIndex - 1);
leftNode.getEntries().add(parentEntry);
for (int i = 0; i < node.getEntries().size(); i++) {
leftNode.getEntries().add(node.getEntries().get(i));
leftNode.getChildren().add(node.getChildren().get(i));
node.getChildren().get(i).setParent(leftNode);
}
leftNode.getChildren().add(node.getChildren().get(node.getChildren().size() - 1));
node.getChildren().get(node.getChildren().size() - 1).setParent(leftNode);
node.setParent(null);
parent.getChildren().remove(nodeIndex);
parent.getEntries().remove(nodeIndex - 1);
}
}
} else {
//entry进入右兄弟
if (parent == this.root && parent.getEntries().size() == 1) {
Node<K, V> rootRightChild = parent.getChildren().get(nodeIndex + 1);
rootRightChild.getEntries().add(0, parent.getEntries().get(0));
for (int i = 0; i < node.getEntries().size(); i ++) {
rootRightChild.getEntries().add(0, node.getEntries().get(node.getEntries().size() - 1 - i));
}
if (!node.isLeaf()) {
for (int i = 0; i < node.getChildren().size(); i ++) {
rootRightChild.getChildren().add(0, node.getChildren().get(node.getChildren().size() -1 - i));
node.getChildren().get(node.getChildren().size() - 1 - i).setParent(rightNode);
}
}
//以下操作,方便虚拟机回收
//node和root的关系
this.root.getChildren().remove(0);
node.setParent(null);
//node和子节点的关系
for (Node<K, V> kvNode : node.getChildren()) {
kvNode.setParent(rootRightChild);
}
node.getChildren().clear();
//right和root的关系
this.root.getChildren().clear();
this.root = rootRightChild;
rootRightChild.setParent(null);
return this.root;
} else {
if (node.isLeaf()) {
Entry<K, V> parentEntry = parent.getEntries().get(nodeIndex);
rightNode.getEntries().add(0, parentEntry);
for (int i = 0; i < node.getEntries().size(); i++) {
rightNode.getEntries().add(0, node.getEntries().get(node.getEntries().size() - 1 - i));
}
//node删除,父节点的children处理
node.setParent(null);
parent.getChildren().remove(nodeIndex);
parent.getEntries().remove(nodeIndex);
} else {
Entry<K, V> parentEntry = parent.getEntries().get(nodeIndex);
rightNode.getEntries().add(0, parentEntry);
for (int i = 0; i < node.getEntries().size(); i++) {
rightNode.getEntries().add(0, node.getEntries().get(node.getEntries().size() - 1 - i));
rightNode.getChildren().add(0, node.getChildren().get(node.getChildren().size() -1 - i));
node.getChildren().get(node.getChildren().size() -1 - i).setParent(rightNode);
}
rightNode.getChildren().add(0, node.getChildren().get(0));
node.getChildren().get(0).setParent(rightNode);
node.setParent(null);
parent.getChildren().remove(nodeIndex);
parent.getEntries().remove(nodeIndex);
}
}
}
}
return parent;
}
private void leftRotate(Node<K, V> node, int indexOfParent) {
Node<K, V> parent = node.getParent();
Entry<K, V> parentEntry = parent.getEntries().get(indexOfParent);
Node<K, V> rightNode = parent.getChildren().get(indexOfParent + 1);
Entry<K, V> rightNodeFirstEntry = rightNode.getEntries().get(0);
List<Entry<K, V>> entries = node.getEntries();
//entries.set(entries.size() - 1, parentEntry);
entries.add(parentEntry);
parent.getEntries().set(indexOfParent, rightNodeFirstEntry);
rightNode.getEntries().remove(0);
if (!node.isLeaf()) {
rightNode.getChildren().get(0).setParent(node);
node.getChildren().add(rightNode.getChildren().get(0));
rightNode.getChildren().remove(0);
}
}
private void rightRotate(Node<K, V> node, int indexOfParent) {
Node<K, V> parent = node.getParent();
Entry<K, V> parentEntry = parent.getEntries().get(indexOfParent - 1);
Node<K, V> leftNode = parent.getChildren().get(indexOfParent - 1);
Entry<K, V> leftNodeLastEntry = leftNode.getEntries().get(leftNode.getEntries().size() - 1);
List<Entry<K, V>> entries = node.getEntries();
entries.add(0, parentEntry);
parent.getEntries().set(indexOfParent - 1, leftNodeLastEntry);
leftNode.getEntries().remove(leftNode.getEntries().size() - 1);
if (!node.isLeaf()) {
leftNode.getChildren().get(leftNode.getChildren().size() - 1).setParent(node);
node.getChildren().add(0, leftNode.getChildren().get(leftNode.getChildren().size() - 1));
leftNode.getChildren().remove(leftNode.getChildren().size() - 1);
}
}
}
5)BTreeTest
import java.util.ArrayList;
import java.util.List;
public class BTreeTest {
public static void test01(){
BTree<Integer, Integer> btree = new BTree<Integer, Integer>(5);
List<Integer> insertList = new ArrayList<Integer>();
insertList.add(10);
insertList.add(20);
insertList.add(30);
insertList.add(40);
insertList.add(50);
insertList.add(60);
insertList.add(70);
insertList.add(80);
insertList.add(90);
insertList.add(100);
insertList.add(110);
insertList.add(120);
insertList.add(130);
insertList.add(140);
insertList.add(150);
insertList.add(160);
insertList.add(170);
insertList.add(81);
insertList.add(82);
insertList.add(83);
insertList.add(84);
insertList.add(85);
insertList.add(86);
insertList.add(141);
insertList.add(142);
insertList.add(143);
insertList.add(144);
insertList.add(145);
insertList.add(146);
insertList.add(9);
insertList.add(51);
insertList.add(99);
insertList.add(147);
insertList.add(171);
insertList.add(87);
insertList.add(88);
insertList.add(89);
insertList.add(171);
insertList.add(172);
insertList.add(173);
insertList.add(71);
insertList.add(72);
insertList.add(73);
insertList.add(101);
insertList.add(102);
insertList.add(21);
insertList.add(22);
insertList.add(148);
insertList.add(149);
insertList.add(52);
insertList.add(53);
insertList.add(161);
insertList.add(162);
insertList.add(163);
insertList.add(174);
insertList.add(175);
insertList.add(176);
insertList.add(1);
for (int i = 0; i < insertList.size(); ++i) {
Integer r = insertList.get(i);
Entry entry = new Entry<Integer, Integer>();
entry.setKey(r);
entry.setValue(r);
btree.insert(entry);
}
btree.output();
List<Integer> deleteList = new ArrayList<Integer>();
deleteList.add(10);
deleteList.add(20);
deleteList.add(30);
deleteList.add(40);
deleteList.add(50);
deleteList.add(60);
deleteList.add(70);
deleteList.add(80);
deleteList.add(90);
deleteList.add(100);
deleteList.add(110);
deleteList.add(120);
deleteList.add(130);
deleteList.add(140);
deleteList.add(150);
deleteList.add(160);
deleteList.add(170);
deleteList.add(81);
deleteList.add(82);
deleteList.add(83);
deleteList.add(84);
deleteList.add(85);
deleteList.add(86);
deleteList.add(141);
deleteList.add(142);
deleteList.add(143);
deleteList.add(144);
deleteList.add(145);
deleteList.add(146);
deleteList.add(9);
deleteList.add(51);
deleteList.add(99);
deleteList.add(147);
deleteList.add(171);
deleteList.add(87);
deleteList.add(88);
deleteList.add(89);
deleteList.add(171);
deleteList.add(172);
deleteList.add(173);
deleteList.add(71);
deleteList.add(72);
deleteList.add(73);
deleteList.add(101);
deleteList.add(102);
deleteList.add(21);
deleteList.add(22);
deleteList.add(148);
deleteList.add(149);
deleteList.add(52);
deleteList.add(53);
deleteList.add(1);
deleteList.add(161);
deleteList.add(162);
deleteList.add(163);
deleteList.add(174);
deleteList.add(175);
deleteList.add(176);
for(int i = 0; i < deleteList.size(); ++i) {
Integer res = deleteList.get(i);
Entry entry = new Entry<Integer, Integer>();
entry.setKey(res);
entry.setValue(res);
btree.delete(entry);
}
//
// Entry entry = new Entry<Integer, Integer>();
// entry.setKey(10);
// entry.setValue(10);
// btree.deleteNode(entry);
System.out.println("----------------------");
btree.output();
System.out.println("----------------------");
// SearchResult<Integer, Integer> result86 = btree.searchfromRoot(86);
// System.out.println(result86.getValue()+ " index: "+result86.getIndex() + " addr: " + result86.getNode());
// SearchResult<Integer, Integer> result142 = btree.searchfromRoot(142);
// System.out.println(result142.getValue()+ " index: "+result142.getIndex() + " addr: " + result142.getNode());
//
// SearchResult<Integer, Integer> result143 = btree.searchfromRoot(143);
// System.out.println(result143.getValue()+ " index: "+result143.getIndex() + " addr: " + result143.getNode());
//
// SearchResult<Integer, Integer> result145 = btree.searchfromRoot(145);
// System.out.println(result145.getValue()+ " index: "+result145.getIndex() + " addr: " + result145.getNode());
//
// SearchResult<Integer, Integer> result146 = btree.searchfromRoot(146);
// System.out.println(result146.getValue()+ " index: "+result146.getIndex() + " addr: " + result146.getNode());
//
// SearchResult<Integer, Integer> result147 = btree.searchfromRoot(147);
// System.out.println(result147.getValue()+ " index: "+result147.getIndex() + " addr: " + result147.getNode());
// SearchResult<Integer, Integer> result160 = btree.searchfromRoot(170);
// System.out.println(result160.getValue()+ " index: "+result160.getIndex() + " addr: " + result160.getNode());
}
public static void test02(){
BTree<Integer, Integer> btree = new BTree<Integer, Integer>(4);
for (int i = 1; i <= 100; i ++) {
Entry entry = new Entry<Integer, Integer>();
entry.setKey(i);
entry.setValue(i);
btree.insert(entry);
}
btree.output();
for(int i = 0; i <= 100; ++i) {
Entry entry = new Entry<Integer, Integer>();
entry.setKey(100 - i);
entry.setValue(100 - i);
btree.delete(entry);
}
System.out.println("----------------------");
btree.output();
System.out.println("----------------------");
}
public static void main(String[] args){
//test01();
test02();
}
}
致谢:
- B树和B+树的插入、删除图文详解
- b树的原理以及实现(第一章)
- 画图软件processon
这篇文档,我利用工作之余花了10天写完,写代码花了4天,画图花了6天(画图真的很方便理解),学习的时候如果有不懂的地方,建议画图,眼高手低容易出问题。本文如果对你真的有帮助的话,不妨帮我点击下致谢3的画图软件,帮他推广下,毕竟白嫖了人家那么久,顺便帮我增加三个文件,谢谢你看到这里,嘻嘻!!!