题目描述

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例：

输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 （股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3。

思路描述

动态规划

考虑到「不能同时参与多笔交易」，因此每天交易结束后只可能存在手里有一支股票或者没有股票的状态。

定义状态dp[i][0]表示第i天交易完手里没有股票的最大利润，dp[i][1]表示第i天交易完手里持有一支股票的最大利润。

考虑dp[i][0]的转移方程，如果这一天交易完后手里没有股票，那可能的转移方程状态为前一天以及么有股票，也可以即dp[i-1][0]，或者前一天结束的时候手里持有一支股票，dp[i-1][1]，这时候我们要将其卖出，并获得prices[i]的收益。因此收益最大化，我们列出如下的转移方程：

$dp[i][0]=max({dp[i?1][0], dp[i?1][1]+prices[i]})$

再来考虑 $d p [i] [1]$ ，按照同样的方式考虑转移状态，那么可能的转移状态为前一天已经持有一支股票， $d p [i ? 1] [1]$ ，或者前一天结束时还没有股票， $d p [i ? 1] [0]$ ，这时候我们要将其买入，并减少 $\textit{prices}[i]$ 的收益。可以列出如下的转移方程：
$dp[i][1]=max({dp[i?1][1],dp[i?1][0]?prices[i]})$

对于初始状态，根据状态定义我们可以知道第 0 天交易结束的时候： $d p [0] [0] = 0 ， d p [0] [1] = ? p r i c e s [0]$

因此，我们只要从前往后依次计算状态即可。由于全部交易结束后，持有股票的收益一定低于不持有股票的收益，因此这时候 $\textit{dp}[n-1][0]$ 的收益必然是大于 $\textit{dp}[n-1][1]$ 的，最后的答案即为 $\textit{dp}[n-1][0]$ .

class Solution {
    public int maxProfit(int[] prices) {
		int n = prices.length;
		int[][] dp = new int[n][2];
		dp[0][1] = -prices[0];
		for (int i = 1; i < n; i++) {
			dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
			dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
		}
		return dp[n-1][0];
    }
}

复杂度分析

时间复杂度： $O (n)$ ，其中 n 为数组的长度。一共有 2n 个状态，每次状态转移的时间复杂度为 O(1)，因此时间复杂度为 O(2n)=O(n)。
空间复杂度：O(n)。我们需要开辟 O(n) 空间存储动态规划中的所有状态。如果使用空间优化，空间复杂度可以优化至 O(1)。

贪心

贪心的角度考虑我们每次选择贡献大于 00 的区间即能使得答案最大化，因此最后答案为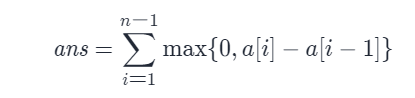在这里插入图片描述

其中 n 为数组的长度。

需要说明的是，贪心算法只能用于计算最大利润，计算的过程并不是实际的交易过程。

在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices) {
        int ans = 0;
        int n = prices.length;
        for (int i = 1; i < n; ++i) {
            ans += Math.max(0, prices[i] - prices[i - 1]);
        }
        return ans;
    }
}