 ??
??
欢迎回到:遇见蓝桥遇见你,不负代码不负卿!
目录
?【声明】
开头笔者要向铁汁们致歉,我没有把这些知识点顺序安排好,因为我也是刚写博客一个多月,所以很多东西正在慢慢熟悉,很抱歉给铁汁们带来不便,后面笔者会尽力整改,等到基础知识点讲解完,后面写的蓝桥冲刺部分会灰常正规,抱拳了哈诸位。
【前言】
对于数据结构这块的话,蓝桥杯考的其实不是很多,但是二叉树是必考的数据结构,没有之一!当然后面还有一个高阶数据结构叫并查集,其实就是树的升级版本——森林,之后再说。所以二叉树这块特别特别重要,笔者也花了老长时间整理才出这篇博文,方便各个知识储备层次上的铁汁都能学到东西。OK,废话不多说,走着。
 ??
??
皮一下很开心哈哈,记得好好学习哦!OK,这次真的来了。?
一、 树的概念及结构(简单了解)
大家简单了解一下下面的知识点,主要是为了方便后面刷题!
1.树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的?
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。

下面注意一下何为树与非树?

下面介绍一些具体的小概念:?
?
- 节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的度为6
- 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;如上图:树的高度为4
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是一个森林)
2.树的表示
typedef int DataType;
struct Node
{
struct Node* firstChild1; ? ?// 第一个孩子结点
struct Node* pNextBrother; ? // 指向其下一个兄弟结点 ? ?
DataType data; ? ? ? ? ? ? ? // 结点中的数据域
};具体表示如下图所示:

OK,上面就简单介绍一些树的相关概念,现在轮到二叉树咯,笔者这里给出的二叉树概念比较精练,都需要掌握哦,因为挑的是最重要的部分,其实也不多啦,我们都可以搞定的,快去康康吧!?
?
二、二叉树的概念及结构
1.二叉树的特点
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点;
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
来康康现实里程序员眼中的二叉树:

emmm...这树长得很有个性鸭
下面看看两种特殊的二叉树叭,学校里期末考试特喜欢考!可以说是数据结构必考题(不难,不信朝后看)
2.特殊的二叉树
<1>.满二叉树
一个二叉树, 如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说, 如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树( 等比数列求和,别告诉我你忘了,我也是百度的(笑哭) )

<2>.完全二叉树
完全二叉树是由满二叉树而引出来的。对于深度为K且 有 n 个结点的二叉树, 当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树 。 要注意的是满二叉树是一种特殊的完全二叉树。
可能描述的还是有点抽象,没事儿,请朝后看,看着看着就明白啦。?


<3>.二叉搜索树
左子树都比根要小,右子树都比根要大!
优点:在二叉搜索树中查找一个数,最多查找高度次,时间复杂度是O(N)

?3.二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构
这里就详细介绍链式结构:
用链表来表示一棵二叉树,即用链表来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域, 左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。 链式结构又分为二叉链和三叉链, 当前我们学习中一般都是二叉链 。

//二叉链
struct BinaryTreeNode
{
struct BinTreeNode* pLeft; ?// 指向当前节点左孩子
struct BinTreeNode* pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}?4.二叉树的性质
性质一:若规定根节点的层数为1,则一棵非空二叉树的第 i 层上最多有 2 ^ (i - 1) 个节点(满二叉树)
性质二:若规定根节点的层数为1,则深度为 h 的二叉树的最大节点数是2 ^ h - 1(满二叉树)
性质三:对任何一棵二叉树,如果度为0的叶节点个数是X0,度为2的节点个数是X2,则 X0 =? X2 + 1;
性质四:若规定根节点的层数是1,具有 n 个节点的满二叉树的深度为 h = log ( n + 1)?
?常考性质题
1.某二叉树共有399个节点,其中199个是度为2的节点,则该二叉树的叶子节点是:___ 个
本题主要考查性质三,X0? = X2 + 1,所以X0 = 200,即叶子结点个数为200个
2.在具有2n 个节点的完全二叉树中,叶子结点个数为:___ 个

说错了,应该是想想为什么?因为鸭,节点不能为负数!?
3.一棵完全二叉树的节点数为531,那么这棵树的高为:(B)
A.11
B.10
C.8
D.12

5.二叉树的遍历
任何一棵二叉树分成三个部分:
1.根节点;
2.左子树;
3.右子树?
分治算法:分而治之,大问题分成类似子问题,子问题再分解成子问题...,直到子问题不可再分解!?一般采用分治算法,也可以说是递归求解二叉树问题。下面是分治算法:
前序(先根)遍历:根节点、左子树、右子树
中序(中根)遍历:左子树、根节点、右子树
后序(后根)遍历:左子树、右子树、根节点
层序遍历:广度优先搜索(BFS)(由近及远、一层一层往外走)
【敲黑板】:
- 前序、中序、后序遍历其实也叫深度优先搜索,一般多是递归!
- 层序遍历采用队列的先进先出的方式,核心思路就是上一层带下一层??

如果理解困难的话,记得笔者在递归章节提到的要画出递归调用图,这样就方便自己理解啦!?
 ??
??
代码实现:
#include<stdio.h>
#include<stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
void PrevOrder(BTNode* root)//前序
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
void InOrder(BTNode* root)//中序
{
if (root == NULL)
{
printf("NULL ");
return 0;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
void PostOrder(BTNode* root)//后序
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}
int main()
{
BTNode* A = (BTNode*)malloc(sizeof(BTNode));
A->data = 'A';
A->left = NULL;
A->right = NULL;
BTNode* B = (BTNode*)malloc(sizeof(BTNode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTNode* C = (BTNode*)malloc(sizeof(BTNode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTNode* D = (BTNode*)malloc(sizeof(BTNode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTNode* E = (BTNode*)malloc(sizeof(BTNode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
PrevOrder(A);
printf("\n");
InOrder(A);
printf("\n");
PostOrder(A);
printf("\n");
return 0;
}常考遍历题
1.某完全二叉树按层次输出(同一层从左到右)的序列为ABCDEFGH,则该完全二叉树的前序序列为:______
建立二叉树如下:

所以,前序遍历为:ABDHECFG?
2.二叉树的前序遍历和中序遍历如下,前序遍历:EFHIGJK,中序遍历:HFIEJKG,请画出这棵二叉树。
【敲黑板】:前序+中序或者后序+中序都可以确定一棵二叉树,但是前序+后续不行,因为前序和后序都可以确定二叉树的根,中序遍历可以分割出左右子树区间。
本题:通过前序遍历可以确定根为E,通过中序遍历可以确定根的左子树是HFI,根的右子树是JKG,然后再结合前序和中序画出二叉树如下:?

3.设一棵二叉树的中序遍历为:badce,后序遍历为bdeca,请画出这棵二叉树。
(本题跟上题一样,在这里就不介绍咯)

OK,开始进入主题了,下面上硬菜!
 ??
??
三、力扣牛客七大热题
前六道题给的是接口型,最后一道是IO型
1.二叉树的最大深度
题目描述:
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
示例:
给定二叉树?[3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7返回它的最大深度为3。
题解:
如果我们知道了左子树和右子树的最大深度是left和right,那么该二叉树的深度是max(left, right) + 1; 而左子树和右子树的最大深度也可以用前面的方法算出。

代码执行:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root){
//找递归边界
if(root == NULL)
{
return 0;
}
//左子树
int leftSum = maxDepth(root->left);
//右子树
int rightSum = maxDepth(root->right);
//注意根节点也要算上
return leftSum > rightSum ? leftSum + 1 : rightSum + 1;
}2.平衡二叉树
题目描述:
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点?的左右两个子树的高度差的绝对值不超过 1 。
示例1:

输入:root = [3,9,20,null,null,15,7]
输出:true示例2:
输入:root = []
输出:true题解:
首先计算左右子树的高度,如果左右子树的高度差是否不超过?1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。
代码执行:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root){
//找递归边界
if(root == NULL)
{
return 0;
}
//左子树
int leftSum = maxDepth(root->left);
//右子树
int rightSum = maxDepth(root->right);
//注意根节点也要算上
return leftSum > rightSum ? leftSum + 1 : rightSum + 1;
}
bool isBalanced(struct TreeNode* root){
if(root == NULL)
{
return true;
}
int leftDepth = maxDepth(root->left);//左子树的深度
int rightDepth = maxDepth(root->right);//右子树的深度
return abs(leftDepth - rightDepth) < 2//保证左右子树深度之差不大于1
&& isBalanced(root->left)//然后再递归下去,再分解成小问题
&& isBalanced(root->right);
}3.二叉树的前序遍历
题目描述:
题目描述:
给你二叉树的根节点?root?,返回它节点值的?前序?遍历。
示例:
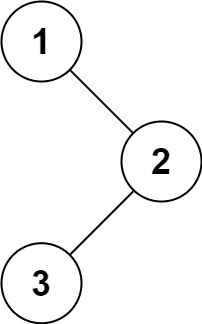
输入:root = [1,null,2,3]
输出:[1,2,3]题解:
我们只要首先将 root 节点的值加入数组,然后递归调用 preorder(root.left) 来遍历 root 节点的左子树,最后递归调用 preorder(root.right) 来遍历 root 节点的右子树即可,递归终止的条件为碰到空节点。
?代码执行:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int* arr = (int*)malloc(sizeof(int) * 100);
*returnSize = 0;
PrevOrder(root, arr,returnSize);
return arr;
}
void PrevOrder(struct TreeNode* root, int* arr, int* returnSize)
{
if(root == NULL)
{
return;
}
arr[(*returnSize)++] = root->val;
PrevOrder(root->left, arr, returnSize);
PrevOrder(root->right, arr, returnSize);
}中序遍历和后序遍历跟前序遍历差不多,铁汁们自己先联系一下,之后再来看看我写的答案。?
4.二叉树的中序遍历
题目描述:
给定一个二叉树的根节点?root?,返回它的?中序?遍历。
示例:

输入:root = [1,null,2,3]
输出:[1,3,2]代码执行:
5.二叉树的后序遍历
题目描述:
给定一个二叉树,返回它的?后序?遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]代码执行:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int* arr = (int*)malloc(sizeof(int)*100);
*returnSize = 0;
PostOrder(root, arr, returnSize);
return arr;
}
void PostOrder(struct TreeNode* root, int* arr, int* returnSize)
{
if(root == NULL)
{
return;
}
PostOrder(root->left,arr,returnSize);
PostOrder(root->right, arr,returnSize);
arr[(*returnSize)++] = root->val;
}6.二叉树的层序遍历
题目描述:
给你一个二叉树,请你返回其按?层序遍历?得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
3
/ \
9 20
/ \
15 7返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]?题解:
题目比较简单,思路全写在代码注释里头咯,结合下面的动图思考哈!
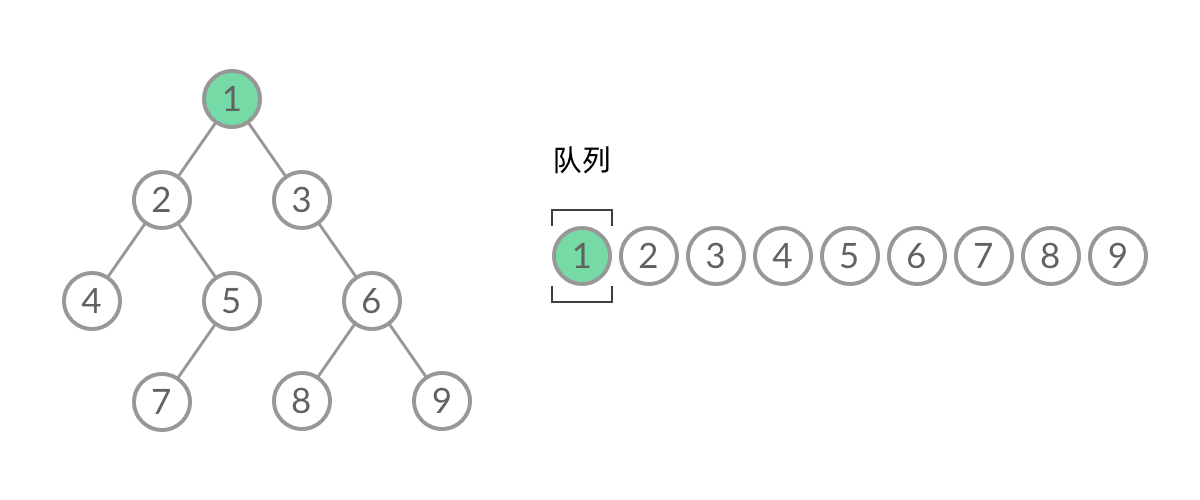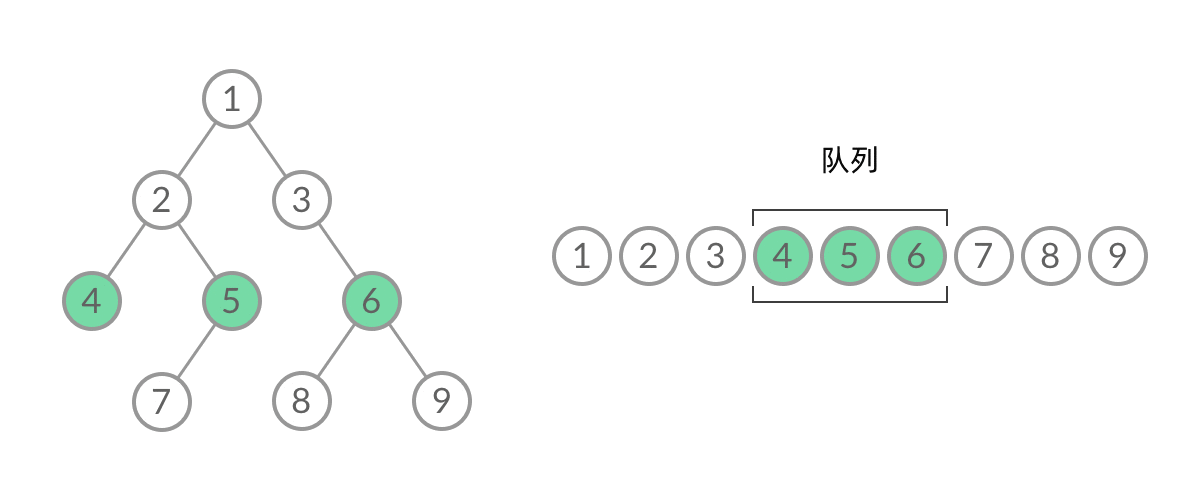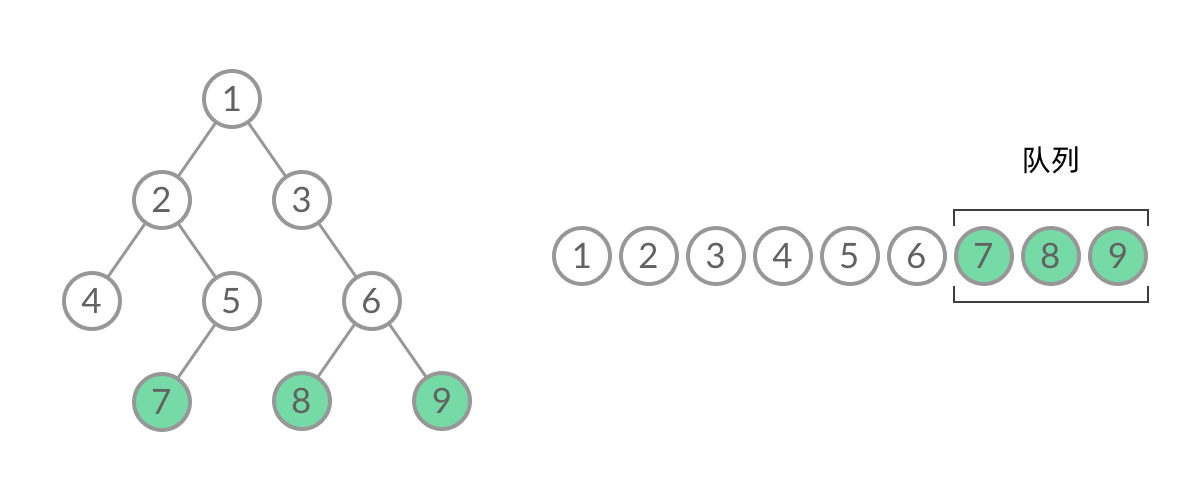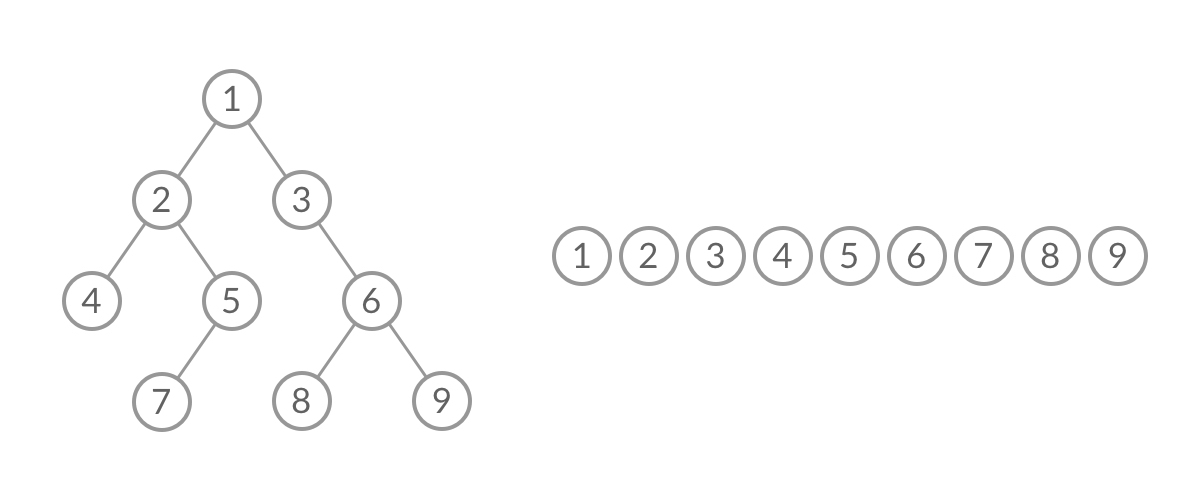
代码执行:
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
class Solution {
public:
/**
*
* @param root TreeNode*
* @return int整型vector<vector<>>
*/
vector<vector<int> > levelOrder(TreeNode* root) {
// write code here
queue<TreeNode*>q;//定义一个队列
if(root)
q.push(root);
vector<vector<int> >ans;//定义一个二维数组用于存放遍历结果
while(!q.empty()){//队列为空时停下来
int n = q.size();
vector<int>tmp;//定义一维数组用于存放每一层的节点
for(int i = 0;i < n;i++){
TreeNode* t = q.front();//访问队首元素
q.pop();//队首元素出队
tmp.push_back(t->val);//将队首元素的值存放到该层的一维数组中
if(t->left)//左子节点入队
q.push(t->left);
if(t->right)//右子节点入队
q.push(t->right);
}
ans.push_back(tmp);//将第一层的一维数组存放二维数组中
}
return ans;
}
};
7.清华大学考研复试题:二叉树遍历
题目描述:
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。?
题解:
如果只给出前序遍历肯定是不能构造一棵二叉树的,但是给出了空树部分就很简单啦。详情见代码哈。
 ?
?
代码执行:
#include<stdio.h>
#include<stdlib.h>
typedef struct TreeNode
{
char val;
struct TreeNode* left;
struct TreeNode* right;
}TNode;
TNode* CreateTree(char* a, int* pi)//创建二叉树
{
if(a[*pi] == '#')//空树不需要构建,但是需要i++走到下一个
{
(*pi)++;
return NULL;
}
//不是空树时就需要构建一棵树
TNode* root = (TNode*)malloc(sizeof(TNode));
if(root == NULL)//检验是否开辟成功
{
printf("malloc fail\n");
exit(-1);
}
root->val = a[*pi];//将此时数组里面的值作为根节点的值
(*pi)++;//i++朝后走
root->left = CreateTree(a, pi);//递归构建左树
//注意哦,此时i不要再++
root->right = CreateTree(a, pi);//递归构建右树
return root;
}
void InOrder(TNode* root)
{
if(root == NULL)
{
return;
}
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
int main()
{
char str[100] = {0};
scanf("%s", str);
int i = 0;
//好好体会为啥传递的是指针--因为要对同一个i进行操作
TNode* root = CreateTree(str, &i);
InOrder(root);
return 0;
}8.补充:求树节点、叶子结点、销毁二叉树
比较简单,上面理解了的话这里就是小case咯。
//树的节点个数
int TreeSize(BTNode* root)//采用的是后序的思维---分治
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;//也可以不用遍历,这样就很简单
//如果不理解,就将递归调用展开图好好理解一下
}
//叶子节点的个数
int TreeLeafSize(BTNode* root)//一定要深刻理解递归
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//销毁一棵二叉树,采用后序的方式,因为鸭,如果直接将根销毁,就会找不到它的左右子树了
void DestoryTree(BTNode* root)
{
if (root == NULL)
{
return;
}
DestoryTree(root->left);
DestoryTree(root->right);
free(root);
root = NULL;
}
四、蓝桥结语:遇见蓝桥遇见你,不负代码不负卿!
参加竞赛获奖是其次的,能在准备的过程中学到东西才是最重要的,毕竟我们的最终目标是找到好点的工作!当然下面的时间节点只针对于不考研的老铁哦。
码字不易,跪求三连鸭。
