[数据结构与算法]leetcode 714

思路一：贪心算法

1.我们将费用纳入买入的成本，维护当前股票买入的成本minPrices，初始值为第一天的股票价格prices[0]+fee。
2.遍历数组，如果prices[i]>minPrices，也就证明了当天股票是可以盈利的，那我们及时将当天的盈利prices[i]-minPrices算入结果res当中，股票成本minPrices=prices[i]，因为之后股票价格可能会越来越高，假设第i+1天股票的价格更高，那么其收益同样可以使用该公式计算。
3.如果prices[i]<minPrices，那我们需要分为两种情况
第一种，就是prices[i]+fee<minPrices，此时是股票购买的更佳时机，此时我们更新minPrices=prices[i]+fee。
第二种，就是prices[i]+fee>=minPrices，因为我们维护的minPrices指的是我们当前持有股票成本，所以成本肯定尽可能越低越好，所以不需要更新成本。

代码一：

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int minPrices=prices[0]+fee;
        int res=0;
        for(int i=1;i<prices.size();i++)
        {
            if(prices[i]>minPrices)
            {
                res+=prices[i]-minPrices;
                minPrices=prices[i];
            }
            else if(prices[i]+fee<minPrices)
            {
                minPrices=prices[i]+fee;
            }
        }
        return res;
    }
};

思路二：

分析：

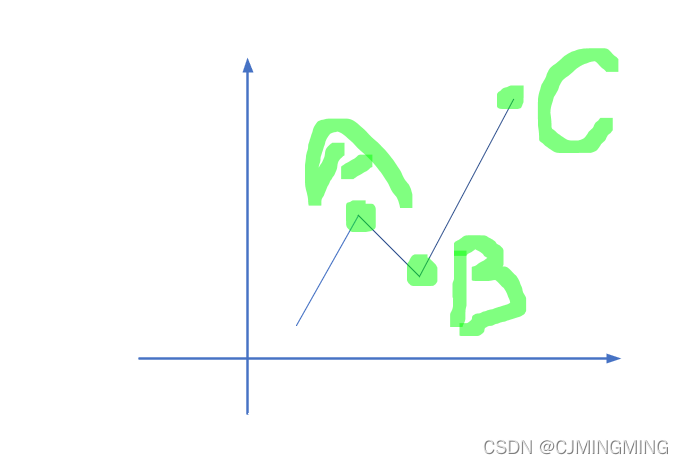
• 如果不考虑手续费的话，要想收益最大，则要抓住每个上升的小区段，如图，那就是A买B卖，C买D卖。

• 如果考虑手续费，那么B就不一定需要卖出了，频繁的卖出增加手续费反而得不偿失。那如何判断B是否该卖出？那就需要考虑到C的买入价格了。

• 我们将手续费归入到买入价格当中，如果prices[C]+fee>prices[B]，那么没必要在B处卖出。

  1.我们维护一个成本minPrices，当前最佳卖出点价格maxPrices，两者初始值为prices[0]+fee。
  2.从第二天开始，如果当天股票价格prices[i]比最佳卖出点价格maxPrices更高，则更新最佳卖出点价格。 反之更低的话，那么考虑是否要在当前最佳卖出点卖出股票

• 依据是：
  如果maxPrices+fee>prices[i]，那么就在最佳当前卖出点抛出，这样就能够通过尽可能多的利用上升小区段的利润。
  反之不予处理。

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int minPrices=prices[0]+fee;
        int maxPrices=prices[0]+fee;
        int res=0;
        for(int i=1;i<prices.size();i++)
        {
            if(maxPrices<prices[i])
            {
                maxPrices=prices[i];
            }
            else if(maxPrices>prices[i]+fee)
            {
                if(maxPrices>minPrices)
                {
                    res+=maxPrices-minPrices;
                }
                maxPrices=minPrices=prices[i]+fee;
            }
        }
        if(maxPrices>minPrices)
        {
            res+=maxPrices-minPrices;
        }
        return res;
    }
};