[数据结构与算法]搜索引擎（六）-- 矩阵分解

一、引言

在搜索引擎（五）中我们提到了推荐系统中矩阵的稀疏问题，很多数据或者用户的交互数据过少，并且有部分交互数据也存在信息冗余的情况。因此，我们需要用矩阵降维的方法，将矩阵投射到对结果有影响的最重要的因素中，并基于此构建新的评价方法。
除此以外，在此前提到的Memory-Based推荐里，我们常常也需要去评价物品或用户的相似度，这些物品或用户也有许多attributes，需要我们进一步进行指标压缩，对属性表进行降维后更方便相似度的对比。譬如一个文档-关键词的特征表。
本文章将对SVD和SVD++两种方法展开进行描述。

二、奇异值分解SVD

SVD可以将一个较大的矩阵分解为多个方便计算和存储的矩阵，目前许多矩阵分解算法都是基于SVD完成的。假设A矩阵是被正则化过的一个大小为$m\times n$的待分解矩阵，我们定义A的SVD分解为$$A=U\Sigma V^T$$
其中$U$是一个$m\times m$的方阵；$\Sigma$是一个$m\times n$的矩阵，除了主对角线上的元素外，所有的值为0；$V$是一个$n\times n$的方阵。$U$和$V$都是酉矩阵，满足$U^T=U^{?1}$和$V^T=V^{?1}$。$\Sigma$矩阵对角线上保存着A矩阵的各个矩阵特征值的根号（又称作奇异值），并且从上到下一般是以降序方式排列的。

在多数情况中，$\Sigma$矩阵中最大的奇异值往往是最能影响矩阵结果的，所以我们在作矩阵近似时，可以只取最大的几个奇异值，以及其对应的$U$和$V$数据进行计算。譬如我们如果只取$k$个最大的奇异值，那么$A_{m\times n}$矩阵可以被近似为
$$A_{m\times n}^{\prime }=U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$

我们如果从向量空间来看这个问题，可以把SVD看作一个矩阵被分解为多个垂直的向量基底的线性组合。而我们的降维就是把最能代表这个矩阵的几个基底留下，剩下的基底全部丢掉的，从而产生新的评价矩阵的过程。

三、SVD的变种

基于机器学习的SVD

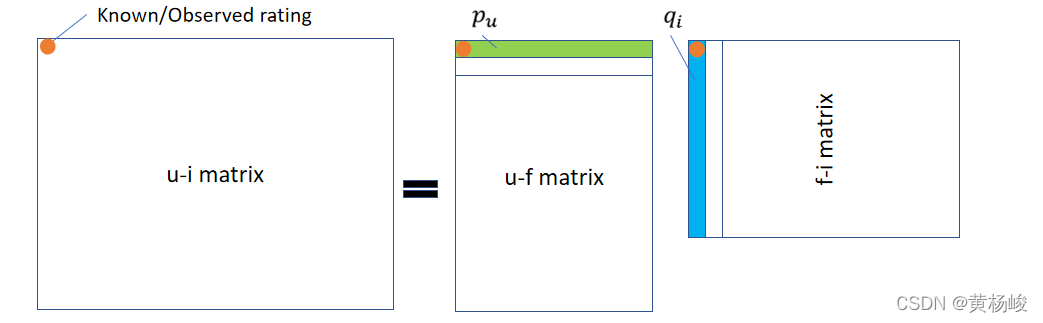
用代数方法求得$U$、$\Sigma$和$V$的过程是十分昂贵的，需要消耗大量时间和空间计算$A$的特征值和特征向量。除此之外，在Memory-Based的推荐系统中，A矩阵是确定的，物品或用户的各个属性一般都是已经采集过，并且不易改变的（如文章的词频），但基于协同过滤的推荐系统中，user-item矩阵不完整，用户可能根本没有跟部分物品交互过，所以靠代数方法并不能获得具体数据。在这类背景下，用机器学习的方法学习到分解矩阵是更好的选择。由于机器学习不关心具体的特征向量，我们可以把$\Sigma$这个值融合到$U$或$V$当中。这里用评分矩阵$r$代替原来的$A$，我们可以把新的分解表示为$r_{m\times n}=P_{m\times f}^T{Q}_{f\times n}$，用户$u$对物品$i$的喜好预测值可以被表示为${\hat{r}}_{u,i}=q_i^T{p}_u$

在最基础的分解中，损失函数可以表示为预测值与真实值的误差$$\sum _i\sum _u(r_{u,i}?q_i^T{p}_u)$$

正则化因子

为了减轻过拟合问题，在某些研究又引入了正则化因子，损失函数变为$$E=\sum _{(u,i)\in \kappa }(r_{u,i}?q_i^T{p}_u)+\lambda (||q_i|{|}^2+||q_u|{|}^2)$$

Bias SVD

有些用户可能对物品评价严格，也有些用户可能对物品的评价很宽容，同时有些物品可能会更容易令用户满意，有些物品更难达到用户心中预期。有学者根据此提出了bias SVD，引入了平均分$\mu$，物品偏差$b_u$和用户偏差$b_i$到预测之中，此时的预测值可以表示为$${\hat{r}}_{u,i}=q_i^T{p}_u+\mu +b_u+b_i$$
损失函数则可以表示为
$$E=\sum _{(u,i)\in \kappa }(r_{u,i}?q_i^T{p}_u?\mu ?b_u?b_i)+\lambda (||q_i|{|}^2+||q_u|{|}^2+b_u^2+b_i^2)$$

Time SVD

而由于用户的喜好是根据时间而变化的，对于我们可以把预测值和相关参数改写为时变函数。$${\hat{r}}_{u,i}(t)=q_i^T{p}_u(t)+\mu +b_u(t)+b_i(t)$$

SVD++

到这里，我们已经提及了不少基于机器学习的矩阵分解方法。我们即将介绍本篇文章的主角–SVD++，它是基于上述矩阵方法的一个改良版，在Netflix评分预测比赛中，SVD++凭借其优秀的性能力压群雄，夺得桂冠，斩获百万美元大奖。
SVD++在上述SVD模型的基础上，引入了隐式反馈值，使得用户的历史浏览数据，用户历史评分数据，电影的历史浏览数据，电影的历史评分数据能成为新的参数，有效解决了冷启动问题。我们用$N(u)$表示用户$u$的行为物品集。每个物品$i$的隐式反馈为$x_i$，用户$u$对于物品及N(u)的兴趣，可以表示为$\frac{{\sum }_{j\in N(u)}{x}_j}{|N(u)|}$；同时，物品$a$被用户关注的预测函数可以被改为$${\hat{r}}_{u,i}=q_i^T{p}_u+\mu +b_u+b_i+\frac{{\sum }_{j\in N(u)}{x}_j}{|N(u)|}$$
损失函数为$$E=\sum _{(u,i)\in \kappa }(r_{u,i}?q_i^T(p_u+\frac{{\sum }_{j\in N(u)}{x}_j}{|N(u)|})?\mu ?b_u?b_i)+\lambda (||q_i|{|}^2+||q_u|{|}^2+b_u^2+b_i^2)$$
这里的隐式因子也可以是关于用户u的属性，如果考虑到用户$u$的其他属性$a$，我们引入关于$a$的隐式因子$y_a$，隐式反馈值为$\frac{{\sum }_{a\in A(u)}{y}_a}{|N(u)|}$，最终的预测值可以表示为$${\hat{r}}_{u,i}=q_i^T{p}_u+\mu +b_u+b_i+\frac{{\sum }_{j\in N(u)}{x}_j}{|N(u)|}+\frac{{\sum }_{a\in A(u)}{y}_a}{|N(u)|}$$

训练过程

我们一般用梯度下降法或迭代的最小二乘法求解，或者是更高级的优化器，如随机梯度下降法（Stochastic Gradient Descent）。此处以梯度下降法为例子，假设需要更新的参数为$q_i$，那么更新的函数可以被表示为
$$\begin{array}{rl}{q}_i(t+1)& =q_i(t)+\alpha \frac{?E}{?q_i(t)}\\ & =q_i(t)+\alpha ((r_{ui}?{\hat{r}}_{u,i})p_u(t)+\lambda q_i(t))\end{array}$$
此处$\alpha$为学习率，当待学习的参数收敛，或者loss函数收敛，我们就可以终止学习了。