一、二叉树的遍历
按照某条搜索路径访问树中每个结点,使得每个结点均被访问。主要分为先序遍历,中序遍历,后序遍历,层序遍历
二、先序遍历
2.1手算
考试一般给一个树的形状,写出他的先序遍历
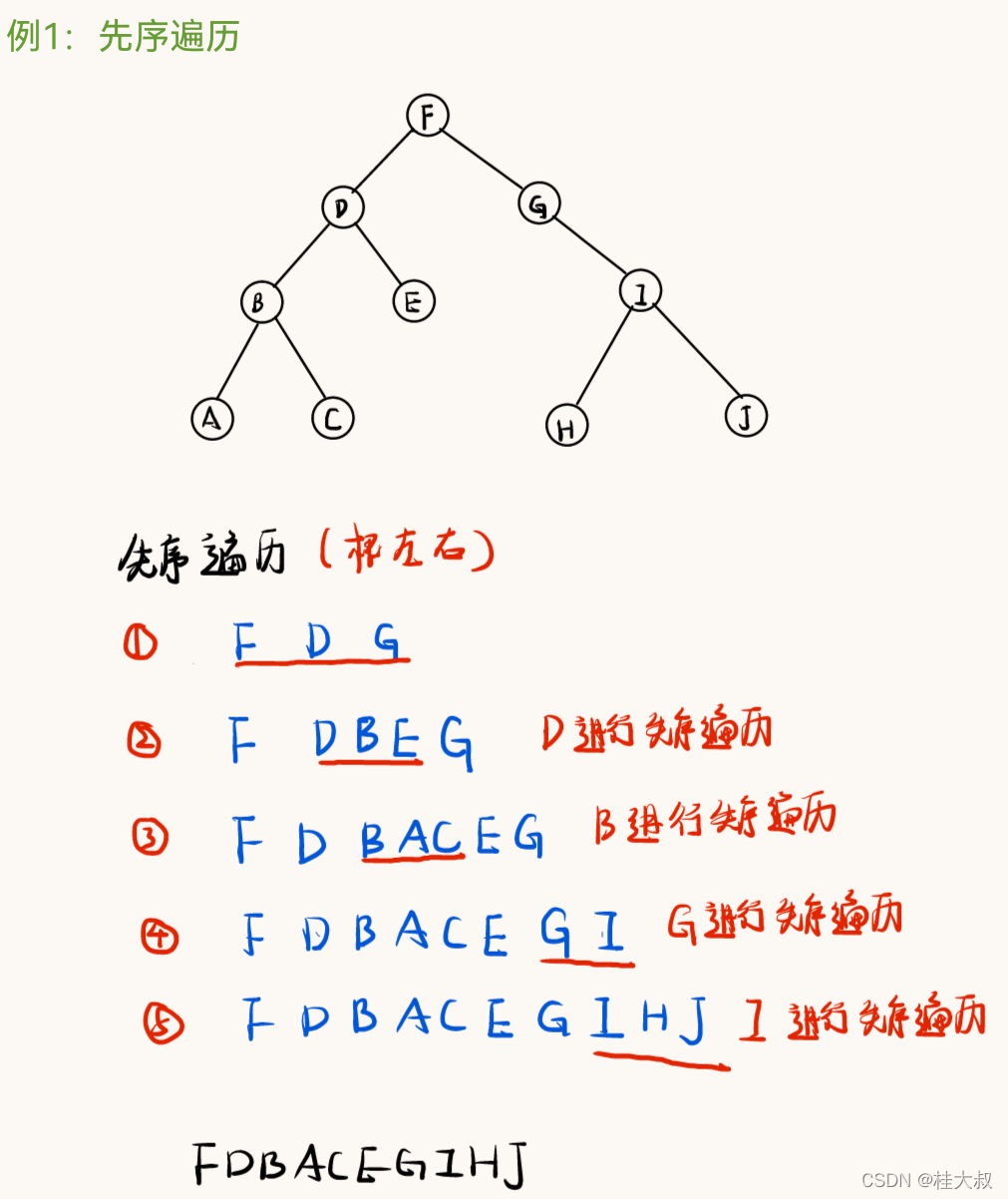
2.2 代码
- 递归先序遍历代码
void PreOrder(BiTree T){
if(T!=NULL)
visit(T);//访问根结点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
- 非递归先序遍历代码
void PreOrder2(BiTree T){
InitStack(S);//初始化栈S;
BiTree p = T;//初始化p是遍历指针
while(p||!IsEmpty(S)){ //栈不空或p不空时循环
if(p){ //一路向左
visit(p); //访问当前结点
Push(S,p); //当前结点入栈
p=p->lchild; //左孩子不空,一直往左走
}
else{ //出栈,并转向栈结点的右子树
Pop(S,p); //栈顶元素出栈
p=p->rchild;//向右子树走,p赋值为当前结点的右孩子
} //返回while循环继续进入if-else语句
}
}
三、中序遍历
3.1 手算
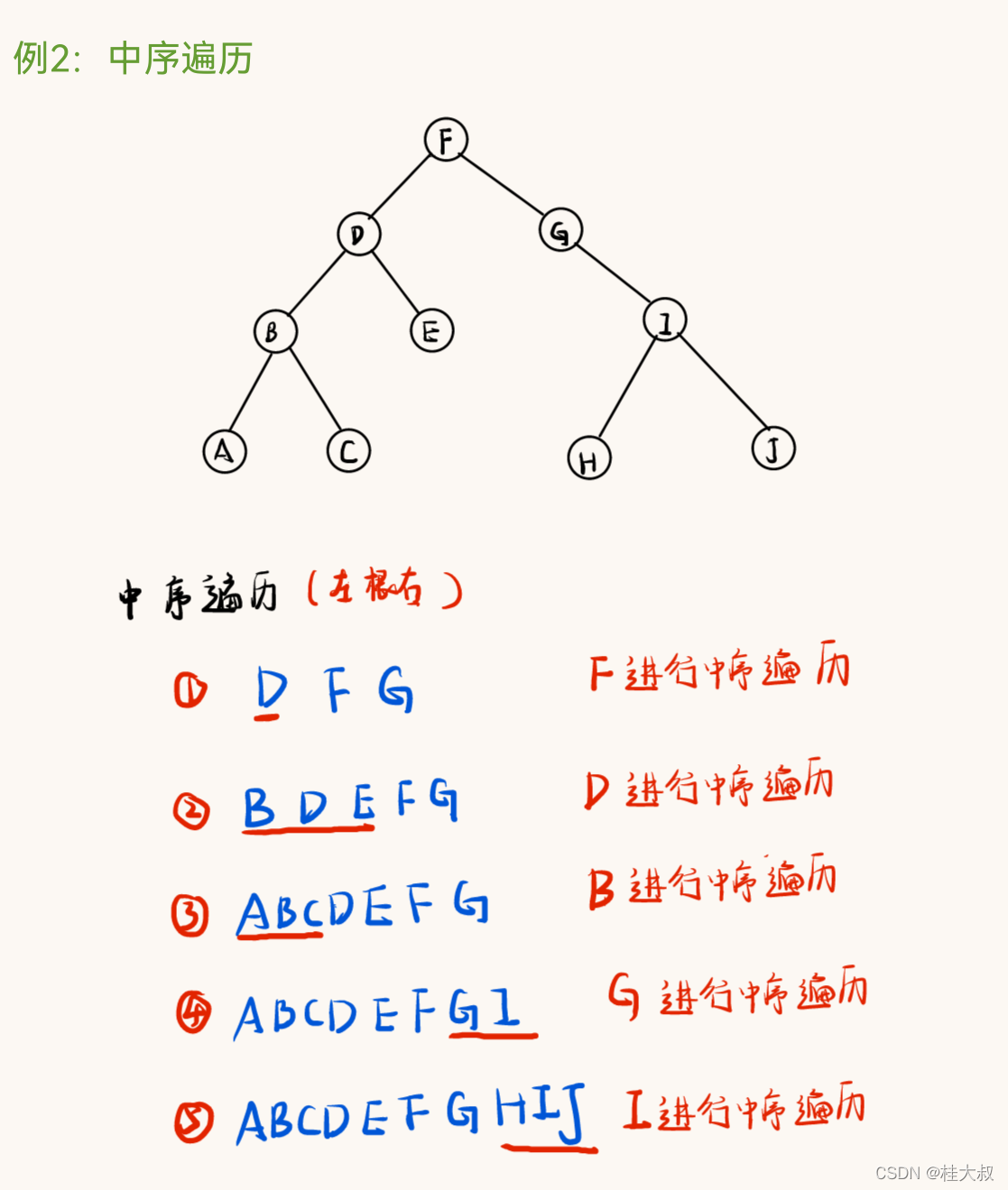
3.2 代码
- 递归中序遍历代码
void InOrder(BiTree T){
if(T!=NULL)
InOrder(T->lchild); //递归遍历左子树
visit(T);//访问根结点
InOrder(T->rchild); //递归遍历右子树
}
- 非递归中序遍历代码
void InOrder2(BiTree T){
InitStack(S);//初始化栈S;
BiTree p = T;//初始化p是遍历指针
while(p||!IsEmpty(S)){ //栈不空或p不空时循环
if(p){ //一路向左
Push(S,p); //当前结点入栈
p=p->lchild; //左孩子不空,一直往左走
}
else{ //出栈,并转向栈结点的右子树
Pop(S,p); //栈顶元素出栈
visit(p); //访问出栈结点
p=p->rchild;//向右子树走,p赋值为当前结点的右孩子
} //返回while循环继续进入if-else语句
}
}
四、后序遍历
4.1 手算
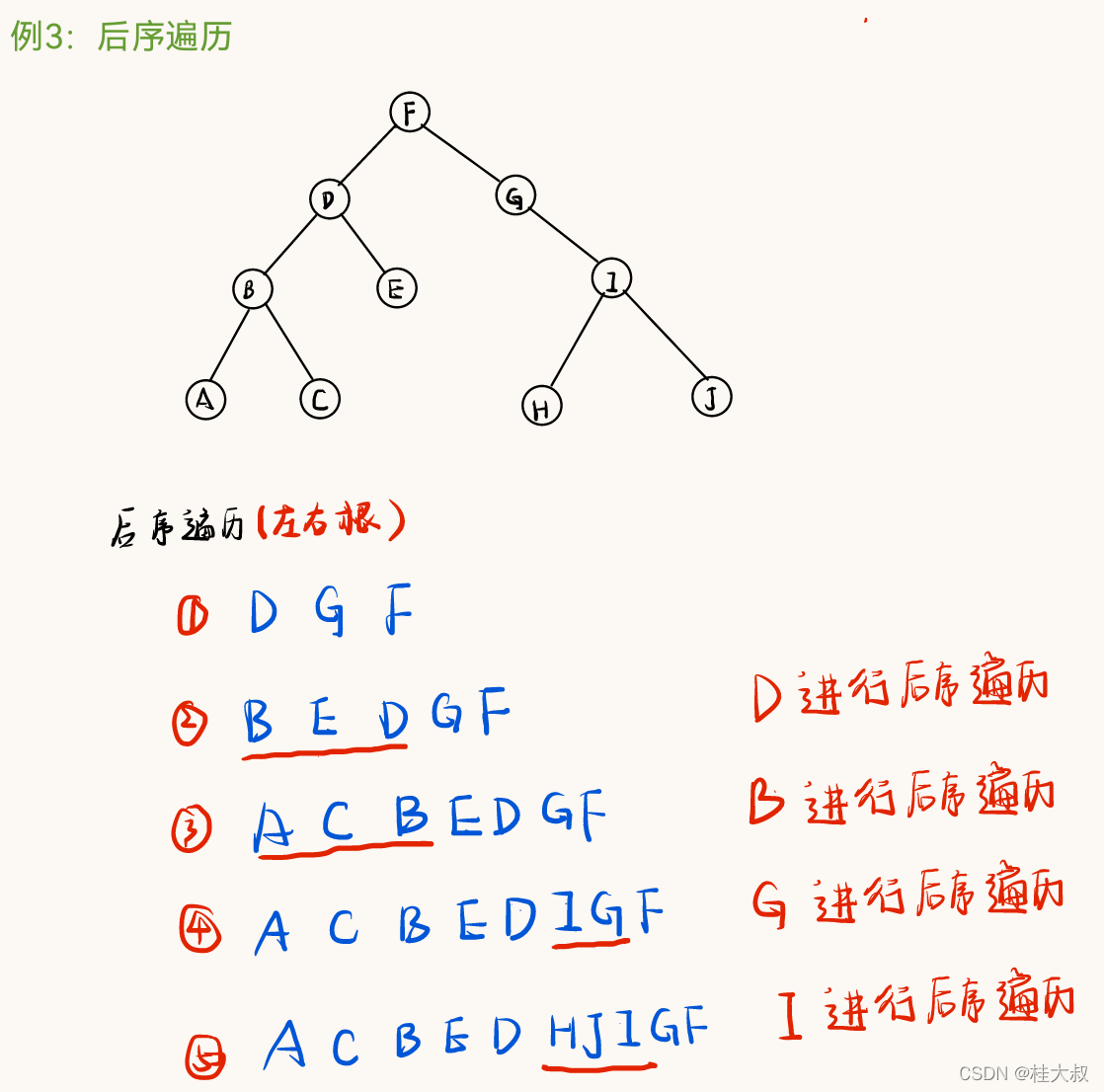
4.2 代码
- 递归后序遍历代码
void PostOrder(BiTree T){
if(T!=NULL)
visit(T);//访问根结点
PostOrder(T->lchild); //递归遍历左子树
PostOrder(T->rchild); //递归遍历右子树
}
- 非递归后序遍历代码
void PostOrder2(BiTree T){
InitStack(S);//初始化栈S;
BiTree p = T;//初始化p是遍历指针
while(p||!IsEmpty(S)){ //栈不空或p不空时循环
if(p){ //一路向左
Push(S,p); //当前结点入栈
p=p->lchild; //左孩子不空,一直往左走
}
else{ //向右
GetTop(S,p); //读栈顶结点(非出栈)
if(p->rchild &&p->rchild!=r) //若右子树存在,且未被访问过
p = p->rchild; //转向右
else{ //否则,弹出结点并访问
pop(S,p); //将结点弹出
visit(p->data); //访问该结点
r = p; //记录最近访问过的结点
p=NULL; //结点访问完后,重置p指针
} //else
} //while
}
五、 层序遍历
5.1 手算

5.2 代码
void LevelOrder(BiTree T){
InitQueue(Q); //初始化辅助队列
BiTree p;
EnQueue(Q,T); //将根结点入队
while(!IsEmpty (Q)){//队列不空则循环
DeQueue(Q,p);//队头结点出队
visit(p); //访问出队结点
if(p->lchild !=NULL) //左子树不空,则左子树根结点入队
EnQueue(Q,p->lchild);
if(p->rchild !=NULL) //右子树不空,则右子树根结点入队
EnQueue(Q,p->lchild);
}
}
六、由遍历构造二叉树
6.1 考法1
中序遍历+前,后,层序遍历中的任何一个即可构成二叉树。
考试经常会给出两个序列(其中有一个必定时中序遍历)然后画出一个二叉树或者再推另外一个遍历
- 例题

6.2 常见挖坑选择题
- 设a,b为一棵二叉树上的两个结点,在中序遍历时,a在b前面的条件是 a在b的左方。
- 任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序不改变。
- n和m为一颗二叉树上的两个结点,中序遍历时,n在m前的条件是n是m的祖先
- n和m为一颗二叉树上的两个结点,后序遍历时,n在m前的条件是n是m的子孙
- 前序遍历与后序遍历相反,如前序遍历ABC,后序遍历CBA,说明该树只有度为1的树
七、线索二叉树
7.1 基本概念
- 所谓二叉树遍历是将二叉树中所有结点排成一个序列。
- 在普通二叉树遍历中,尤其是二叉链表,它只能表示一种父子关系。不能把体现出元素的前驱后继的关系。
- 含n个结点的二叉树中,有 n+1 个空指针。
7.2 结点结构及结构体代码

typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild,*rchild;//左右孩子指针
int ltag,rtag; //左右线索标志0表孩子,1表示指针
}ThreadNode,*ThreadTree;
7.3 手写构造线索二叉树(常考)
经典例题,这题会了基本上可以解决大部分手算题目
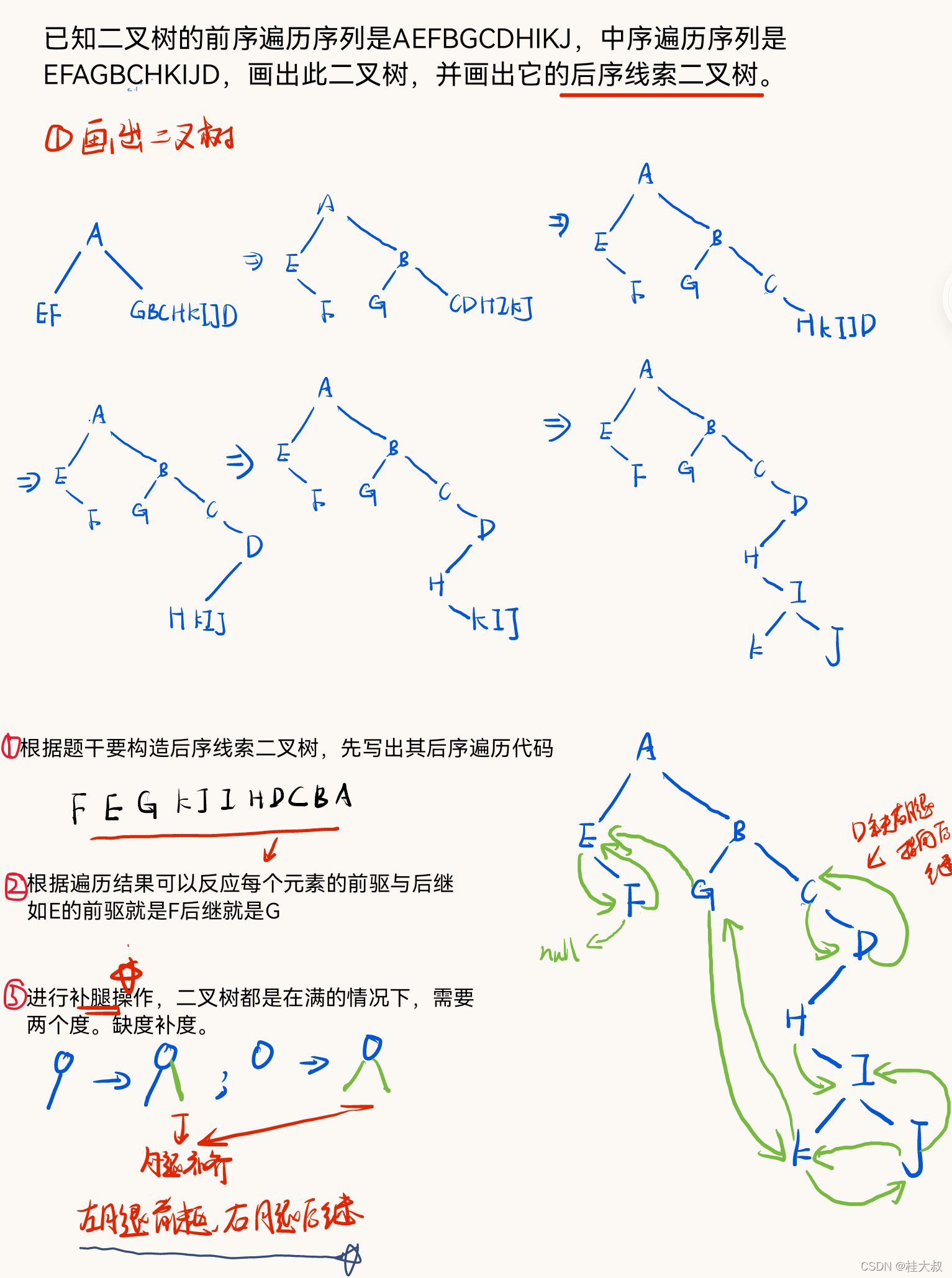
7.4 线索二叉树的遍历
在这里插入代码片