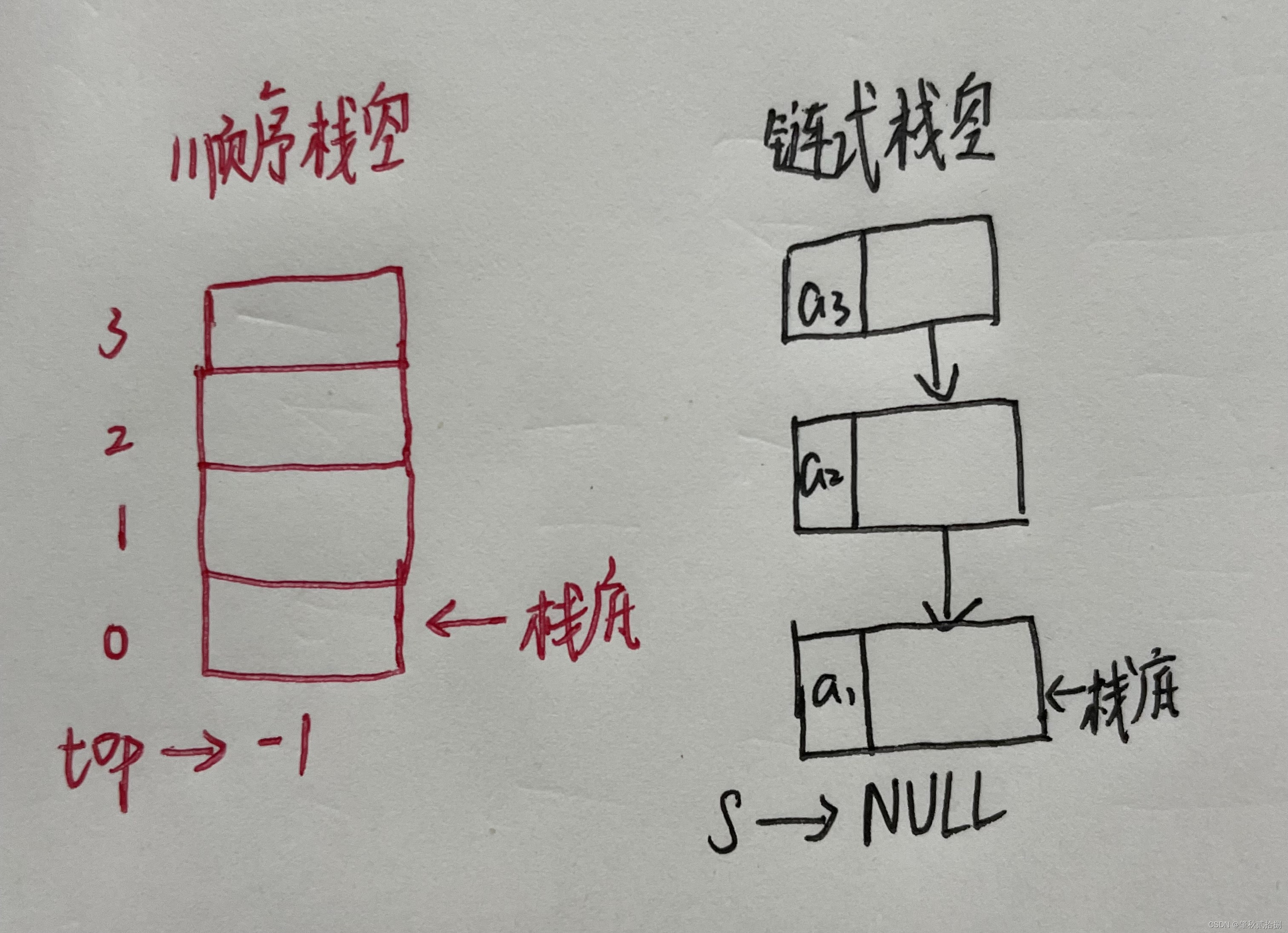
🎆了解顺序栈和链式栈

在数据结构的世界中，栈和顺序表以及链表（链式存储结构）一样，都是线性的存储结构。而栈是一种运算受限的线性表（逻辑结构概念）。而它运算的特殊性就在于其"后进先出"的特性。打个比方就是，你在餐桌上不断的放餐盘，而你拿这些餐盘的时候，你只能从你刚刚放入的最顶上的餐盘开始。
而你每次放盘的那个顶端就叫做栈顶（Top）,也就是线性表允许插入和删除的一端。
放在最底下的盘子，叫做栈底（Bottom），也就是不允许插入和删除的另一端。
栈底固定，栈顶浮动。当栈中元素个数为零时，这个栈就叫做空栈。而插入的操作一般叫做进栈（push），而删除的操作（从栈中提取指定元素）叫做出栈（pop）。

现在在介绍栈具体实现的两种方式。众所周知，所有的数据结构都跟链表和数组有着莫大的关联。而栈也是如此。而采用顺序储存的栈就叫做顺序栈，借助数组来存放其从栈底到栈顶的各个数据。而链式栈就是用借助链表实现，我们通常将链表的头部作为栈顶，将尾部作为栈底。
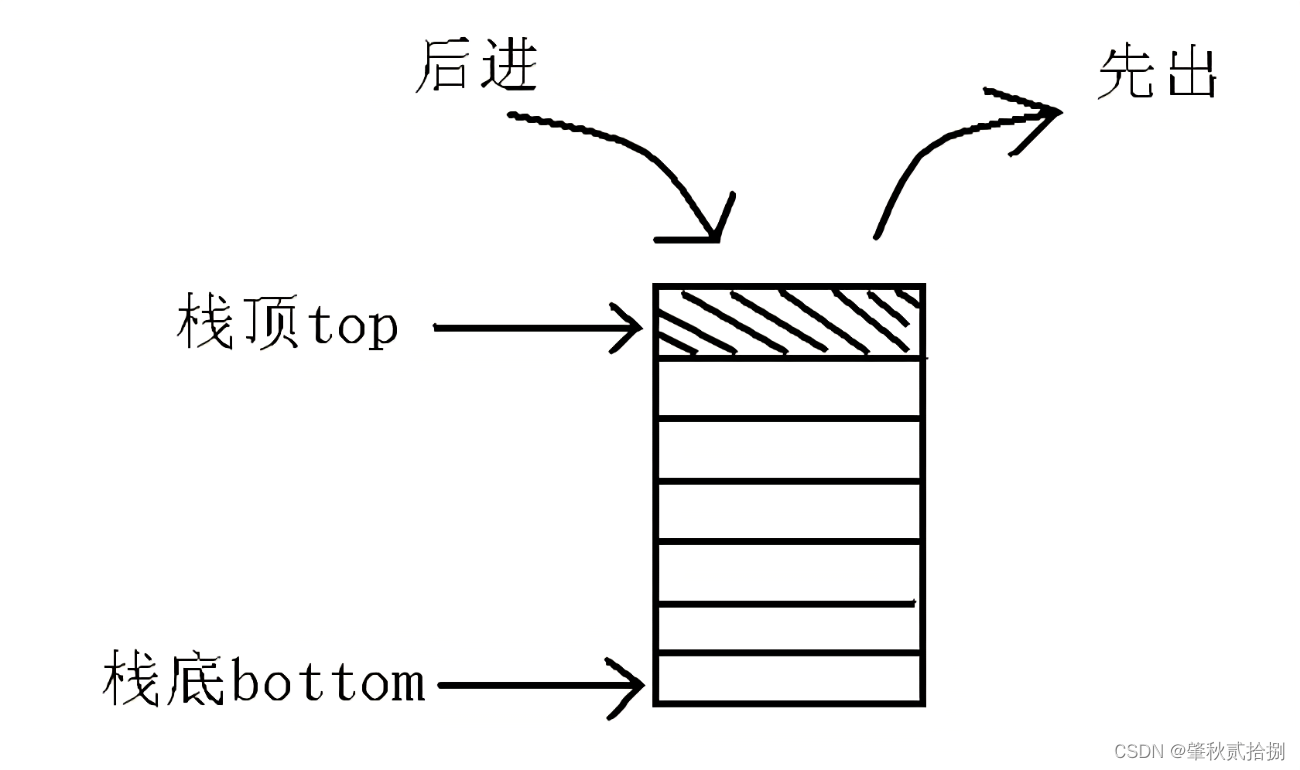
请添加图片描述

🎆栈的初始化和建立

👇顺序栈

首先我们介绍顺序栈的初始化以及简易的相关操作，在开始看代码前我们需要了解一下几个关键点。
1.顺序栈是一个结构体，内部由一个int类型的变量和一个存放某种数据类型的数组。

#define MAXsize 20//栈中的最大元素
typedef int Elemtype;//数据结构中常用的数据元素类型定义方式
//【👇】下面是顺序栈的定义
typedef struct odstack {
	Elemtype data[MAXsize];
	int top;//top就是栈顶指针（表示当前栈顶元素的下标）
}ODstack;

2.看到代码里面的top这个变量，他就是这个栈的栈顶指针（top表示的是当前栈顶元素的下标）
3.对于顺序的简单操作介绍三个（初始化栈，进栈，出栈）
4.因为data[ MAXsize ]是从下标0开始。所以s1->top=-1就表示这个栈为空栈，而s1->top=MAXsize-1就表示这个栈为满栈。
5.初始化：就是把栈内的top值等于-1
6.压栈：判断是否满栈，不是就top先加1，后入栈
7.出栈：判断是否空栈，不是就先出栈，再top-1
来看看代码实现👇👇👇👇👇👇👇

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

#define MAXsize 20//栈中的最大元素
typedef int Elemtype;//数据结构中常用的数据元素类型定义方式
//【👇】下面是顺序栈的定义
typedef struct odstack {
	Elemtype data[MAXsize];
	int top;//top就是栈顶指针（表示当前栈顶元素的下标）
}ODstack;

//栈的初始化【👇】
bool initODstack(ODstack* s1) {
	s1->top = -1;
	return true;
}//让栈顶指针先为-1


//入栈【👇】
bool push(ODstack* s1,Elemtype newdata) {//newdata为要压入栈的新元素
	if (MAXsize-1==s1->top) return false;
	else s1->data[++s1->top]=newdata;
	return true;
}

//出栈【👇】
bool pop(ODstack* s1,Elemtype *outdata) {//outdata为出栈的元素（用指针为了让这个数能在函数外表示出来）
	if (-1 == s1->top)return false;
	else *outdata = s1->data[s1->top--];
	return true;
}


int main(void) {
	ODstack s1;
	initODstack(&s1);
	int i;
	for (i = 0;i < 6;i++) {
		int newdata;
		scanf("%d", &newdata);
		push(&s1, newdata);
	}

	int length = s1.top;
	for (i = 0;i <= length;i++) {
		Elemtype *outdata=(int*)malloc(sizeof(ODstack));
		pop(&s1, outdata);
		printf("顶层为：%d\n", *outdata);
	}

}

👇链式栈

简单的了解完顺序栈的操作，现在让我们来看看链式栈的相关简单操作。链式栈的的总体思路和顺序栈的相同的，只不过它把链表的头部当作栈顶，把链表的尾部作为栈底。
那么对于这种链式栈，我们如何进行入栈和出栈操作呢。实现入栈就是将数据从链表的头部插入。而实现出栈就是删除链表头部的首元结点。
那么相比顺序栈，链式栈有什么特殊的地方呢。1.不需要头结点。2.因为链表长度是动态的，所以链式栈基本不存在栈满这种情况。3.头指针就是栈顶，空栈相当于头指针指向空。
现在让我们看看链式栈的所有相关操作👇👇👇👇

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

//【链式栈的定义👇】
typedef struct linkstack {
	int data;
	struct linkstack* next; 
}LINKstack;//定义一个链式栈（受限的先入后出的规则让它与链表有本质区别）

//【链式栈的初始化👇】与顺序栈类似
LINKstack* initstack(LINKstack* s) {
	s = NULL;
	return s;
}

//【判断是否为空栈👇】
bool emptystack(LINKstack* s) {
	if (s)return true;
	else return false;
}

为空栈的判断条件是类似的
入栈和出栈👇

//【链式栈的入栈操作👇】
LINKstack* push(LINKstack* s, Elemtype newnum) {
	LINKstack* newstack=(LINKstack*)malloc(sizeof(LINKstack));
	newstack->data = newnum;
	newstack->next = s;
	s = newstack;
	return s;
}

//【链式栈的出栈操作👇】
LINKstack* pop(LINKstack* s,Elemtype *newnum) {
	if (s==NULL) {
		printf("栈已空");
		return NULL;
	}
	else {
		*newnum = s->data;
		LINKstack* p = s;
		s = s->next;
		free(p);
		return s;
	}
}

🎆栈的应用范围

简单的了解完了栈，那我们在什么样的情况下才会使用到栈这种结构呢？

栈可以在函数调用的时候储存断点，函数递归的时候它会发挥巨大的作用。
我们日常生活中上网常使用的浏览器左上角的回退功能，底层就使用了栈存储结构。
括号匹配问题（编译器中检查你写的程序括号正确与否）也是栈结构来实现。
进制转换，表达式求值，逆序输出等等

🎇简单用栈解决问题——（有效的括号）

在两个月前，有一道在力扣上的题目，也就是我们提到的括号匹配问题，就运用到了栈的方法，现在让我们通过具体的例子，更深刻的去理解栈的使用方法

?简易循环实现

对于这道题，如果之前我们还没学习过栈的有关知识也是可以的解决的。首先你需要对例子进行自己观察，你也可以自己手写出更长的有效括号去寻找其中的规律。
你可以发现，在最后一个左括号的右边必须是一个跟他相对应的右括号。同时我们可以定义一个数组来存储之前还没有匹配的左括号，后面的右括号去进行判断。（整个逻辑等于运用循环和数组去模拟了一个栈的思路）
代码如下👇👇

bool isValid(char * s){
  if(strlen(s)%2==1)return false;//如果是奇数很显然直接错误
char l[10000],r[10000];
int i=0,j=0,left=0;//j是右括号这个数组的下标（如果匹配最后j肯定等于left）
while(*s!='\0')//三个判断语句来进行分类
{
    if(*s=='('||*s=='{'||*s=='[')
    {
        l[++i]=*s;
        left++;//统计左括号数目
    }
    else if(*s==')')
    {
        r[j]='(';
        if(r[j]!=l[i])
        return false;
        j++;
        i--;
    }
    else if(*s=='}')
    {
        r[j]='{';
        if(r[j]!=l[i])
        return false;
        j++;
        i--;
    }else if (*s==']')
    {
        r[j]='[';
        if(r[j]!=l[i])
        return false;
        j++;
        i--;
    }
    s++;
}
if(j!=left)return false;//左右括号数不相等

return true;
}

在这里插入图片描述

?利用栈的方法解决

用栈去解决这道题目是最常用也是最好理解的方法，在之前的循环中我们不知不觉就已经摸到了栈的解决方法，现在我们使用栈来更为准确的写一次。
首先我们看一张选自力扣官方答案的图片，它很清楚的展示了栈在这道题上的操作过程。
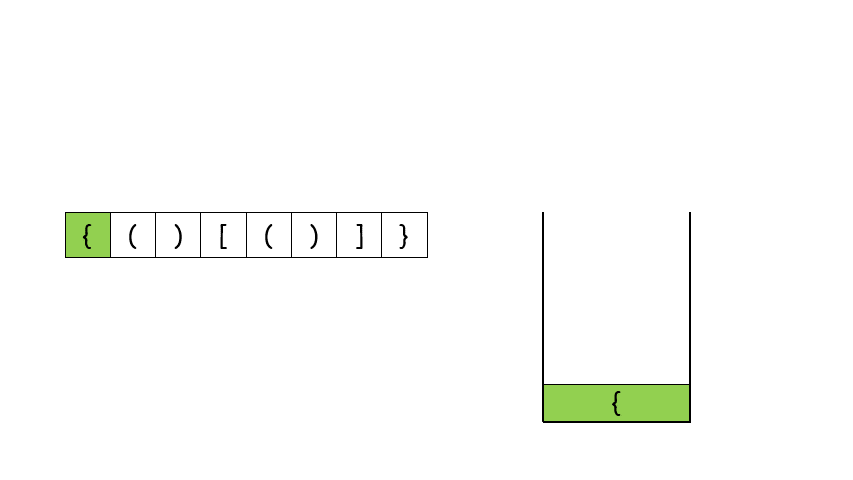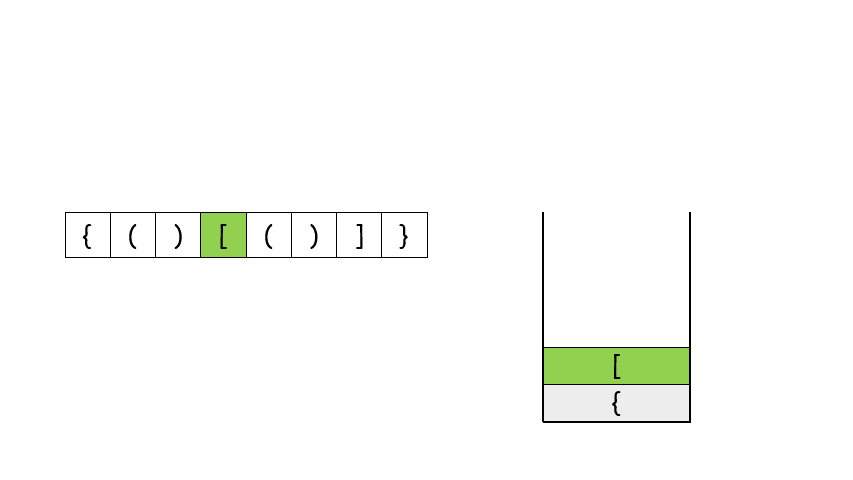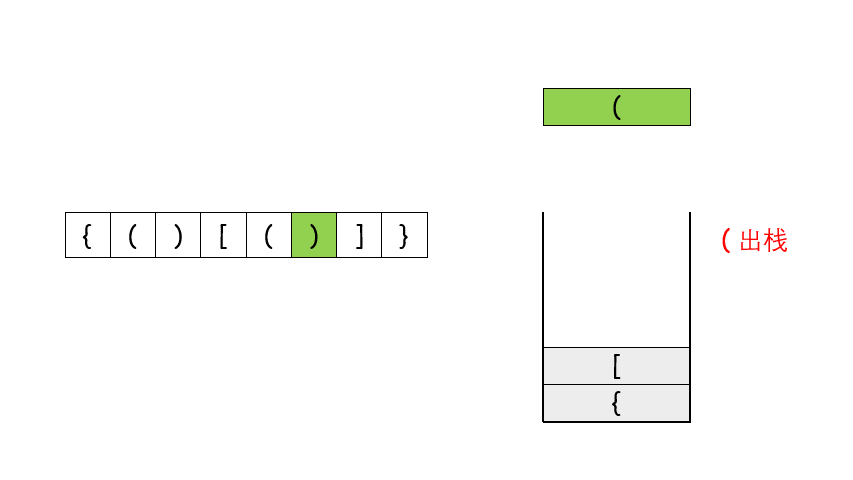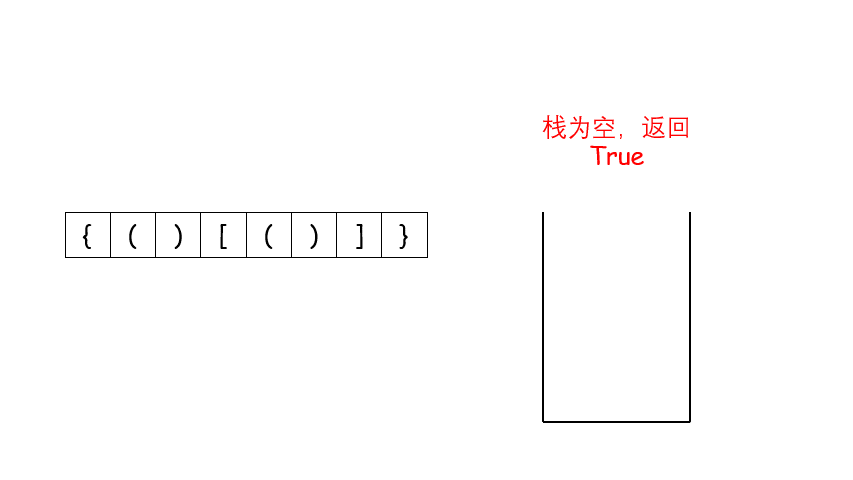
让我们来看代码👇👇👇

char reversech(char s){
    if(s==')')return '(';
    else if(s=='}')return '{';
    else if(s==']')return '[';
    return 0;
}//因为右括号要和左括号作比较，所以定义一个反转字符的函数


bool isValid(char * s){
    int n =strlen(s);
    if(n%2!=0)return false;//特殊情况直接排除
    int i=0;
    char stack[n+1];//定义栈（char类型）
    int top=-1;//栈顶指针（初始化指向-1）
    for(i=0;i<n;i++){
        if(s[i]=='('||s[i]=='{'||s[i]=='['){
            stack[++top]=s[i];//左括号则往栈里填充括号
        }else{
            if(top==-1||stack[top]!=reversech(s[i])) return false;//如果栈已空，却有右括号则错误。
            //最后一个左括号不等于连着的右括号也直接错误
            top--;//如果前面两个不跳出，则top--（改变栈顶指针，模拟出栈）
        }
    }
    return top==-1;//（结尾栈空）
}

在这里插入图片描述

?最长有效括号

通过上面关于栈的应用，我们想必对这个数据结构已经有了方向，那我们在上一题的基础上再增加难度。我们去寻找这整串括号中最长的有效括号。

我们先关注其中的几个关键点
首先有效括号必须以左括号开始
分析几种特殊情况在遇到这种括号时（）（），通过我们分析我们发现，如果我们直接找出一整段有效括号（直到发现无效）是错误的，碰到（）（（）这类情况就可能会错误。什么意思呢，我们不是直接找这个4，而是去进行2+2的操作。
怎么计算当前有效括号的长度？是定义一个curlength=0自增，还是下标相减。
让我们来看一下代码👇👇👇

int longestValidParentheses(char * s){
    if(!s)return 0;

    int length=strlen(s);
    int stack[length+1];//在后文中用来记录这一段有效括号的长度（存储有效括号开始的下标）
    int max=0;//存放最长的有效括号
    int top=-1;//栈顶指针
    int curlength=0;//当前有效括号的长度

    stack[++top]=-1;//++top是因为-1不能做下标，为什么为-1（例子：（）（）  下标为：0 1 2 3 因为0的存在头减尾不等于长度
    //所以要往后移动一位。

    for(int i=0;i<length;i++){

        if(s[i]=='('){//左括号
            stack[++top]=i;//入栈，存储当前括号的下标

        }else{//右括号时(两种可能：1.栈已空（第一个为右括号肯定错误）2.和栈中一个左括号匹配)

            --top;//先对栈顶指针进行自减

            if(top==-1){//满足则表示原来栈就已空(第一个情况)
                stack[++top]=i;//       
            }else{
                curlength=i-stack[top];//这一段有效括号的长度
                if(curlength>max)max=curlength;
            }

        }
    }
    return max;
}