谈谈自己对B、B+树的一些理解

1、二叉查找树 Binary Search Tree

? 在正式谈谈B树、B+树之前先谈谈二叉树，在数据库主流的索引查找方式中，线性查找和二分查找我在这就不过多的赘述了，想必大家也很清楚他们的算法了，但是由于在磁盘中，很多时候我们并不能获取到相当大一片连续的物理空间，在其中碎片是非常多的，所以二分查找在数据量庞大的时候就无法找到中间的数据在哪，这也是二分查找的缺陷所在，因此，发展出了二叉查找树。那二叉树的数据结构如下图所示：
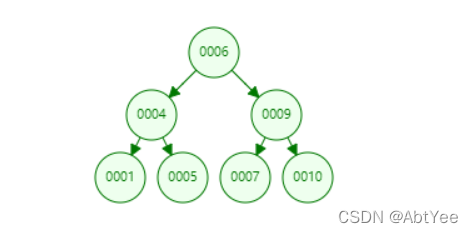
在这里插入图片描述
可以看到，在二叉查找树中，小于根节点的数都会被放到左子树，反之放到右子树，查找的时候也是根据与根节点对比来找到是在左子树还是右子树，在完全二叉树的情况下，他的查找效率和二分查找是一样的，但是，二叉树有一个问题就是他会出现不平衡的情况，也就是出现如下状况：
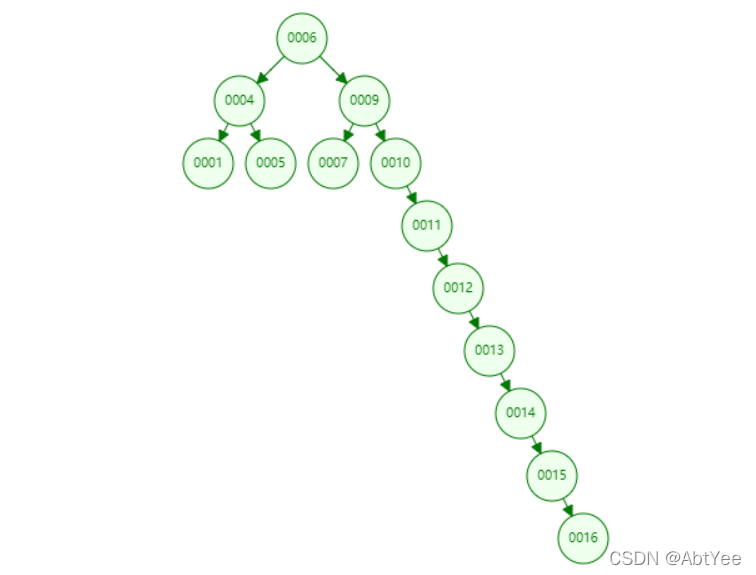
在这里插入图片描述
那么在这种情况下的时候，二叉查找树的查找效率就会退回到了线性查找的效率了，体现不出来树这种结构天然的优势。

2、平衡二叉树 AVL Tree

? 于是，基于二叉树的状况，后来又发展出了平衡二叉树，平衡二叉树的特点是在增删改时它能通过左旋或者右旋来达到二叉树的平衡，不会出现一边过长的状况，而查找的方式和二叉树一样，至于怎么实现这个平衡二叉树，网上很多资料我就不赘述了。
在这里插入图片描述

3、B树

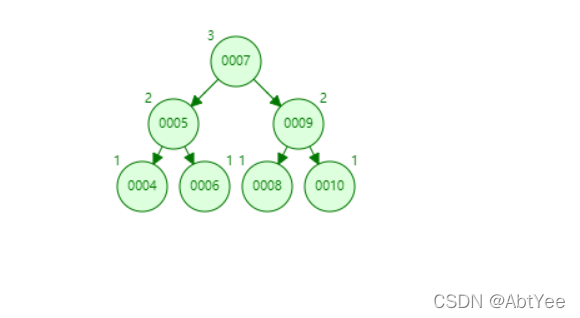
? 那么为什么不用平衡二叉树来作为数据库索引的数据结构呢？其实我们不难发现，在二叉树中，有个致命的缺点就是每一个节点存放的数据量实在是太小了，拿上图举例：
在这里插入图片描述
在每一个节点中，如根节点，我们只存放了id为7的一行数据，但是在内存或者硬盘读写中都有一个最小的基本单位，比如磁盘，磁盘的物理结构来看存取信息的最小单位是扇区，一个扇区就是512字节，而诸如SSD这样的更大，那如果在这么一种情况下存储这一条数据，有两种选择，要么和别的数据一起存储，要么浪费掉剩下的空间就只存这么一条数据。在这种基础上，我们也能很容易的想到，只要在一个节点上放多条数据，这样不就能规避这个问题了，比如我在根节点处放id为7、8、9、10…等的数据，这样一来，空间能被有效利用的同时，我们也能够极大地降低磁盘的读写次数，在二叉树中我们需要一条一条地读取数据，而在我们所设想的这种结构中，一次性就能读取出数条数据，显然效率更高。而这种思路也促成了B树的发展。

? 首先明确一点，B Trees和Binary Tree是两回事，B树中的B并不是Binary。B树是线性结构和树的结合，如下图所示：
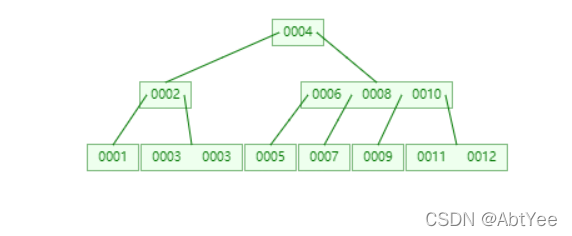
在这里插入图片描述
不难发现，在节点的前后都会有一个指针，一个节点中多条数据的话中间也会存在指针，当我们要查找比如id为7的这条数据时，会先拿7和根节点比较，发现比4大，从右子树查找，而在一个节点中，查找的方式便是线性结构的查找，找到7比6大，比8小，就从8前方的指针处寻找，从而定位到该数据。一句话总结B树的查找方式即为：**从节点外部来看，是以树的形式查找，而节点内部来看是以线性结构查找。**而且，B树也通过多数据节点来大大降低了树的高度，从而减少了磁盘对树高度一次一次遍历的代价，提升了查找的性能。还有一点值得一提的是，B树不需要旋转就可以保证树的平衡。

4、B+树

? 那么这个时候大家都会想到，B树这种数据结构已经很优秀了，为什么还要有B+树呢，B+树又+了什么东西呢。我们现在设想这么一个场景，仍是这B树举例：
在这里插入图片描述
如果这时我需要查找一个id范围在5-9的一段数据，该怎么查找呢？是不是就是从根节点判断5和4，发现比4大，到右子树查找，发现比6小，定位到前面指针下的5处，接着再从根节点比较6和4、7和4…一次一次从根节点向下查找，这时查找效率是非常低的，而且，在实际应用中这种场景也是非常的常见，比如我要查找成绩在60-100之间的学生，20岁-40岁之间的员工等等等等。这时，就发展出了B+树，具体数据结构如下图所示：
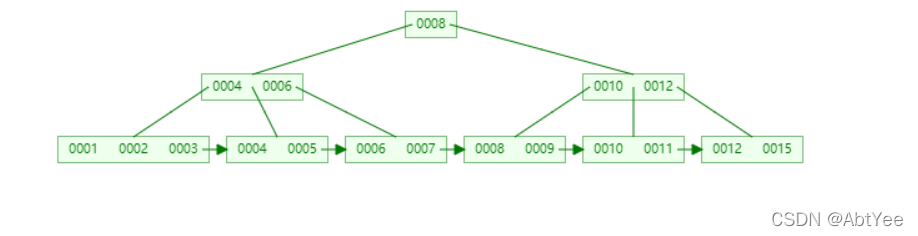
在这里插入图片描述
乍一看，发现好像和B树差不多，同样是有左右子树，每个节点中也同样有好几条数据，但是仔细看就会发现，B+树最底层，也即叶子节点处多了个箭头，而且可以发现，非叶子节点的数据似乎到叶子节点处又出现了一次，但是这并不是重复，而是在B+树中，把索引和数据分开了，非叶子节点存的就是单纯的索引，而数据都在叶子节点处，我们可以通过索引很快的定位到叶子节点的一条数据上，而且，在叶子节点之间又形成了链表，那这么一来，范围查找的效率也会变得相当的高，同样的我们还是查找5-9之间的数据，此时我们从根节点定位到叶子节点的5后，只需线性查找5之后的数据，一直到找到指定的范围，就已经不需要再一次一次地从根节点出发向下查找，不仅提高了范围查找的效率，也保留了B树一个节点中存放了多条数据的优势。