一、填空题(5题,每小题2分,共10分)
二、简答题(3题,每小题5分,共15分)
三、算法填充题(2题,共10空,每空3分,共30分)
子集生成:
给定一个正整数集合{x1,x2,…,xn}和一个正整数y,设计一个回溯算法,求集合X的一个子集Y,使得Y中的元素之和等于y。
算法如下:
输入:数组X,解向量p,开始下标from,目标和y
输出:true或false
1. 若X[from]等于y,则p[from]=1,返回true; //找到
2. 若X[from]大于y,则p[from]=0,返回false; //剪枝回溯
3. 置p[from]=1
??? 3.1 调用本算法,参数X、p、from+1、y-X[from];
??? 3.2 若算法返回true,则找到一组解,返回true;
4. 置p[from]=0
??? 4.1调用本算法,参数X、p、from+1、y;
??? 4.2 若算法返回true,则找到一组解,返回true;
调用算法时,解向量p初始化为0,开始下标为0,目标和为y值
? ?代码:
public boolean reverse(int[] X,boolean[] p,int from,int y){
??? ??? if(X[from] == y){
??????? p[from] = true;
??????? return true;
?? ????}
??? ??? if(X[from] > y){
??????? p[from] = false;
??????? return false;
??? ????}
??? ??? p[from] = true;
??? ??? if(reverse(X,p,from+1,y-X[from]))
??????? ??? return true;
??? ??? p[from] = false;
??? ??? if(reverse(X,p,from+1,y))
??????? ??? return true;
}全排列生成:
给定一个没有重复数字的序列,返回其所有可能的全排列。
算法如下:
全局变量:数组P存放符合条件的结果,对象数组result,存放结果,used Boolean[]数组,判断是否使用过
输入:数组X
输出:无
1.若数组P的长度等于X的长度,则将数组P添加到result数组中
2.循环遍历数组X[i]
2.1如果used[i]为真,则continue
2.2把used[i]置为真,并且将X[i]添加到P中
2.3再次调用本算法
2.4将X[i]从P中移除,将used置为false
class Solution {
??? List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
??? LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
??? boolean[] used;
??? public List<List<Integer>> permute(int[] nums) {
??????? if (nums.length == 0){
??????????? return result;
??????? }
??????? used = new boolean[nums.length];
??????? permuteHelper(nums);
??????? return result;
??? }
??? private void permuteHelper(int[] nums){
??????? if (path.size() == nums.length){
??????????? result.add(new ArrayList<>(path));
??????? ????return;
??????? }
??????? for (int i = 0; i < nums.length; i++){
??????????? if (used[i]){
??????????????? continue;
??????????? }
??????????? used[i] = true;
??????????? path.add(nums[i]);
??????????? permuteHelper(nums);
??????????? path.removeLast();
??????????? used[i] = false;
??????? }
??? }
}最长公共子序列:
????????对给定序列X=(x1, x2,…, xm)和序列Z=(z1, z2,…, zk),Z是X的子序列当且仅当存在一个严格递增下标序列(i1, i2,…, ik),使得对于所有j=1, 2, …, k,有zj=xij(1≤ij≤m)。
??? 给定两个序列X和Y,当另一个序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。最长公共子序列问题就是在序列X和Y的公共子序列中查找长度最长的公共子序列。
解:设?表示子序列和的最长公共子序列的长度。动态规划函数定义为:

状态矩阵定义为:

??? 算法代码:
int CommonOrder(int m, int n, int x[ ], int y[ ], int z[ ])
? {
????? for (j=0; j<=n; j++)?? //初始化第0行
???????? L[0][j]=0;
????? for (i=0; j<=m; i++)?? //初始化第0列
???????? L[i][0]=0;
????? for (i=1; i<=m; i++)
???????? for (j=1; j<=n; j++)
??????????? if (x[i]= =y[j]) { L[i][j]=L[i-1][j-1]+1; S[i][j]=1; }
?????????? else if (L[i][j-1]>=L[i-1][j]) { L[i][j]=L[i][j-1]; S[i][j]=2; }
???????????? else {L[i][j]=L[i-1][j]; S[i][j]=3; }
????? i=m; j=n; k=L[m][n];
?????while(i>0 && j>0)
???? {
????????if (S[i][j]= =1) { z[k]=x[i]; k--; i--; j--; }
??????? else if (S[i][j]= =2) j--;
?????????????? else i--;
???? }
???? return L[m][n];
? }回溯法:
?? 哈密顿回路:假定图G=(V, E)的顶点集为V={1, 2, …, n},则哈密顿回路的可能解表示为n元组X=(x1, x2, …, xn),其中,xi∈{1, 2, …, n} ,并有如下约束条件:? ????
?? ?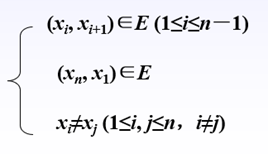
?? 算法8.4——哈密顿回路问题
void Hamiton(int n, int x[ ], int c[ ][ ])?
?//c[ ][ ]存储顶点之间边的情况,x[n]表示哈密顿回路经过的顶点
???? //所有数组下标从1开始
{
???for (i=1; i<=n; i++)?? //初始化顶点数组和标志数组
???{
??????? x[i]=0;
????????visited[i]=0;
???}
???k=1; visited[1]=1; x[1]=1;? //从顶点1出发
???while (k>=1)
???{
???????x[k]=x[k]+1;?? //搜索下一顶点
???????while (x[k]<=n)
???????if (visited[x[k]]= =0 && c[x[k-1]][x[k]]= =1)
???????????break;
???????else x[k]=x[k]+1;
?????? if (x[k]<=n && k= =n && c[x[k]][1]= =1) {
???????????for (k=1; k<=n; k++ )?
???????????cout<<x[k];
???????????return;
???????}
???????else if (x[k]<=n && k<n ) {
??????????? visited[x[k]]=1;
????? ???????k=k+1;
??????? }
???????else{??????????? //回溯
????????????x[k]=0;
????????????visited[x[k]]=0;???
????????????k=k-1;??
???????}
????}
}???
八皇后(N皇后):
在8×8的棋盘上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。可以把八皇后问题扩展到n皇后问题,即在n×n的棋盘上摆放n个皇后,使任意两个皇后都不能处于同一行、同一列或同一斜线上。
??? 算法8.5——n皇后问题??
void Queue(int n)
{
?????? for (i=1; i<=n; i++)??? //初始化
????????? x[i]=0;
?????? k=1;
?????? while (k>=1)
?????? {
??????????? x[k]=x[k]+1;???? //在下一列放置第k个皇后
??????????? while (x[k]<=n && !Place(k))
??????????? x[k]=x[k]+1;???? //搜索下一列
??????????? if (x[k]<=n && k= =n) {?? //得到一个解,输出
???????????????? for (i=1; i<=n; i++)?
???????????????????? cout<<x[i];
??????????? ?????return;
??????????? }
??? ????????else if (x[k]<=n && k<n)
????????????????? k=k+1;????? //放置下一个皇后
????????????else {?????
???????????????????x[k]=0;???? //重置x[k],回溯
??????????????????k=k-1;
????????????}
????????}
??}
bool Place(int k)?? //考察皇后k放置在x[k]列是否发生冲突
{
???for (i=1; i<k; i++)??
???if (x[k]= =x[i] | | abs(k-i)= =abs(x[k]-x[i]))
return false;
return true;
}最大子段和(注意平时作业):

- ?? 分治法:
?? 算法4.7——最大子段和问题
int MaxSum(int a[ ], int left, int right)
{
sum=0;
if (left= =right) { //如果序列长度为1,直接求解
if (a[left]>0) sum=a[left];
else sum=0;
}
else {
center=(left+right)/2; //划分
leftsum=MaxSum(a, left, center); //对应情况①,递归求解
rightsum=MaxSum(a, center+1, right); //对应情况②,递归求解
s1=0; lefts=0; //以下对应情况③,先求解s1
for (i=center; i>=left; i--)
{
lefts+=a[i];
if (lefts>s1) s1=lefts;
}
s2=0; rights=0; //再求解s2
for (j=center+1; j<=right; j++)
{
rights+=a[j];
if (rights>s2) s2=rights;
}
sum=s1+s2; //计算情况③的最大子段和
if (sum<leftsum) sum=leftsum;
//合并,在sum、leftsum和rightsum中取较大者
if (sum<rightsum) sum=rightsum;
}
return sum;
}
//时间复杂度:(nlog2n)
四、综合题(3题,共45分)
??? 贪心法(设计+证明)
?? 设计思路:贪心法在解决问题的策略上目光短浅,只根据当前已有的信息就做出选择,而且一旦做出了选择,不管将来有什么结果,这个选择都不会改变。换言之,贪心法并不是从整体最优考虑,它所做出的选择只是在某种意义上的局部最优。这种局部最优选择并不总能获得整体最优解(Optimal Solution),但通常能获得近似最优解(Near-Optimal Solution)。
???????? 证明:
????????
???????????????????????????????? ?
?
0/1背包问题(证明+动态规划法计算过程):
给定n种物品和一个背包,物品i重量是wi,其价值为vi背包容量为C,对每种物品只有两种选择:装入背包或者不装入背包》如何选择装入背包的物品,使装入背包中物品总价值最大?
证明:

????? 动态规划法计算过程:
令V(i, j)表示在前i(1≤i≤n)个物品中能够装入容量为j(1≤j≤C)的背包中的物品的最大值,则可以得到如下动态规划函数:
????????????????? ?V(i, 0)= V(0, j)=0?
???????? ???????? ????????
?????????
货币兑付问题(证明+动态规划法计算过程):

?
?? 证明:
????????
?? 动态规划法计算过程:
?? 解:仅考虑(v1, v2, …, vn),y为整数的情况(非整数时,可适当转化得到)。不失一般性,假设(v1, v2, …, vn)已经按升序排列。
设?表示使用前种货币支付值货币的最小张数。货币兑付问题递推公式为:

由此设计动态规划算法。

????????
多段图最短路径问题(证明+动态规划法计算过程):
图G=(V, E)是一个带权有向连通图,如果把顶点集合V划分成k个互不相交的子集Vi(2≤k≤n, 1≤i≤k),使得E中的任何一条边(u, v),必有u∈Vi,v∈Vi+m(1≤i<k, 1<i+m≤k),则称图G为多段图,称s∈V1为源点,t∈Vk为终点。多段图的最短路径问题是求从源点到终点的最小代价路径

证明:首先证明多段图问题满足最优性原理。设s, s1, s2, …, sp, t是从s到t的一条最短路径,从源点s开始,设从s到下一段的顶点s1已经求出,则问题转化为求从s1到t的最短路径,显然s1, s2, …, sp, t一定构成一条从s1到t的最短路径,如若不然,设s1, r1, r2, …, rq, t是一条从s1到t的最短路径,则s, s1, r1, r2, …, rq, t将是一条从s到t的路径且比s, s1, s2, …, sp, t的路径长度要短,从而导致矛盾。所以,多段图的最短路径问题满足最优性原理。
动态规划法计算过程:
?? 
? ? ? ?
批处理调度(限界函数设计+搜索过程):
给定n个作业的集合J={J1, J2, …, Jn},每个作业都有3项任务分别在3台机器上完成,作业Ji需要机器j的处理时间为tij(1≤i≤n, 1≤j≤3),每个作业必须先由机器1处理,再由机器2处理,最后由机器3处理。批处理作业调度问题要求确定这n个作业的最优处理顺序,使得从第1个作业在机器1上处理开始,到最后一个作业在机器3上处理结束所需的时间最少
???????? 限界函数设计:
???????? 
???????? 搜索过程:
???????? 
(1)在根结点,将sum1[0]和sum2[0]分别初始化为0;?
(2)在结点2,以作业J1开始处理,则sum1[1]=5,目标函数值为5+(7+5+9+8)+2=36,sum2[1]=5+7=12,将结点2加入待处理结点表PT中;在结点3,以作业J2开始处理, 则sum1[1]=10,目标函数值为10+(7+5+9+8)+5=44,sum2[1]=10+2=12,将结点3加入表PT中;在结点4,以作业J3开始处理,则sum1[1]=9,目标函数值为9+(7+5+9+8)+2=40,sum2[1]=9+9=18,将结点4加入表PT中;在结点5,以作业J4开始处理,则sum1[1]=7,目标函数值为7+(7+5+9+8)+2=38,sum2[1]=7+8=15,将结点5加入表PT中;
(3)在表PT中选取目标函数值极小的结点2优先进行搜索;
(4)在结点6,准备处理作业J2,则sum1[2]=5+10=15,目标函数值为15+(5+9+8)+5=42,sum2[2]=15+5=20,将结点6加入表PT中;在结点7,准备处理作业J3,则sum1[2]=5+9=14,目标函数值为14+(5+9+8)+2=38,sum2[2]=14+9=22,将结点7加入表PT中;在结点8,准备处理作业J4,则sum1[2]=5+7=12,目标函数值为12+(5+9+8)+2=36,sum2[2]=12+8=20,将结点8加入表PT中;
(5)在表PT中选取目标函数值极小的结点8优先进行搜索;
(6)在结点9,准备处理作业J2,则sum1[3]=12+10=22,目标函数值为22+(5+9)+5=41,sum2[3]=22+5=27,将结点9加入表PT中;在结点10,准备处理作业J3,则sum1[3]=12+9=21,目标函数值为21+(5+9)+2=37,sum2[3]=21+9=30,将结点10加入表PT中;
(7)在表PT中选取目标函数值极小的结点10优先进行搜索;
(8)在结点11,准备处理作业J2,则sum1[4]=21+10=31,目标函数值为31+5=36,sum2[4]=31+5=36,由于结点11是叶子结点,并且目标函数值在表PT中最小,则结点11代表的解即是问题的最优解,sum2[4]是机器2完成所有4个作业的时间,则机器3完成所有4个作业的时间是sum2[4]+t23=36+2=38。搜索过程结束。
TSP问题(搜索空间树及算法):
TSP问题是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。
??? 搜索空间树:
??? 
???
??? 算法:
