三、前缀,双指针及递归, 分治

来源
作者: 李煜东
1 前缀和
1.1 前缀和为何?
前缀和是一个数组的某项下标之前(包括此项元素)的所有数组元素的和
| 定义式 | 递推式 | |
|---|---|---|
| 一维前缀和 | S [ i ] = ∑ j = 1 i A [ j ] S[i]=\sum_{j=1}^{i} A[j] S[i]=∑j=1i?A[j] | S [ i ] = S [ i ? 1 ] + A [ i ] \quad S[i]=S[i-1]+A[i] S[i]=S[i?1]+A[i] |
| 二维前缀和 | S [ i ] [ j ] = ∑ x = 1 i ∑ y = 1 j A [ x ] [ y ] S[i][j]=\sum_{x=1}^{i} \sum_{y=1}^{j} A[x][y] S[i][j]=∑x=1i?∑y=1j?A[x][y] | S [ i ] [ j ] = S [ i ? 1 ] [ j ] + S [ i ] [ j ? 1 ] ? S [ i ? 1 ] [ j ? 1 ] + A [ i ] [ j ] S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+A[i][j] S[i][j]=S[i?1][j]+S[i][j?1]?S[i?1][j?1]+A[i][j] |
-
注: 为使
S[0] = 0不越界 即: 递推式中i = 1有(i - 1) = 0, 此处数组 A 从i = 1即(A[1]) 开始, -
一维前缀和:

-
二维前缀和:
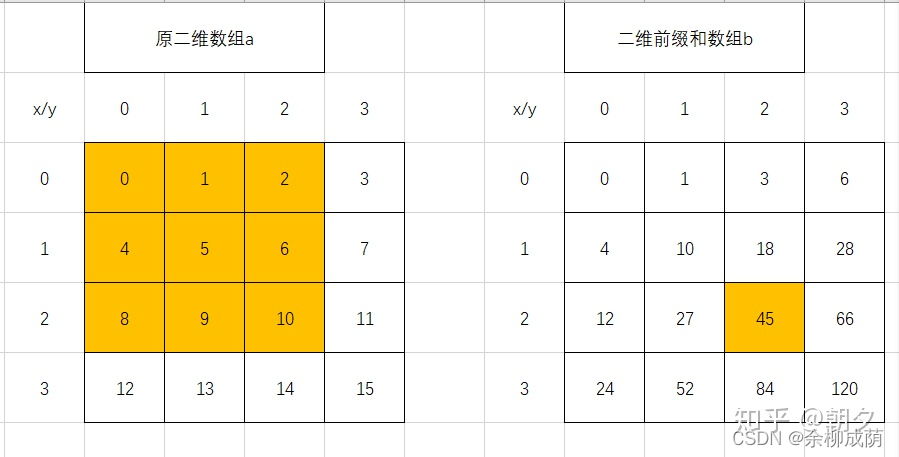
1.2 为何求前缀和?
前缀和是一种预处理,用于降低查询时的时间及空间复杂度。
- 例如求子段和 ------- A中第 L 个数到第 R 个数的和
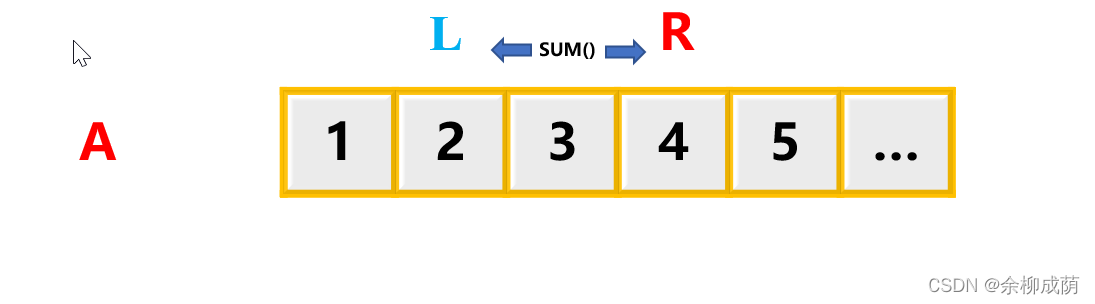
- 如在A中,
n个数访问m次, 求每一次访问的字段和:- 暴力解法: 不需要额外空间, 但每次访问都需计算L, R之间和 >> 时间复杂度大 (大概O(n^2))
- 前缀和: 先计算出O(n)空间复杂度的和S[i], 再利用 S[R] - S[L - 1]计算出每一次访问的子段和, 并直接输出, >>> 时间复杂度O(m + n)
1.3 相关例题
1.3.1 1248 . 统计「优美子数组」
- 思路 子段(区间)对奇、偶数计数 >>> 对元素
%后 的0、1计数
>>> 利用前缀和S[R] - S[L-1] == k条件 >>> 获得所求区间
- 将原数组变为 > 奇数记1, 偶数记为0的数组 , 并计算前缀和 S[:n+1]
- Counter() 统计各S中各项值及数量 >> 最简单哈希
- 遍历S, ans加上j之前
Counter中key等于s[j] - k的统计量
from collections import Counter
class Solution:
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
n = len(nums)
s = [0] * (n + 1)
for i in range(1, n + 1):
s[i] = s[i - 1] + nums[i - 1] % 2
ans = 0
d = Counter(s)
for j in range(1, n + 1):
if s[j] - k >= 0:
ans += d[s[j] - k]
return ans
- 优化 ---- 求前缀和 并根据奇数数量建立计数列表(哈希) — cut
class Solution:
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
n = len(nums)
ans, odd, cut = 0, 0, [0] * (n + 1)
cut[0] = 1 # S[0] = 0 所以代表非奇数的 + 1
for num in nums:
if num & 1:
odd += 1
if odd >= k:
ans += cut[odd - k]
cut[odd] += 1
return ans
1.3.2 53 . 最大子数组和
- 思路 前缀和 + 前缀最小值 >>> S[R] - S[L-1] R作为遍历指针所指位置, 即求S[L - 1]最小值 >>>
S[i] - preMin(i - 1)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
ans = - 100000
preMin = [0] * (n + 1)
s = [0] * (n + 1)
for i in range(1, n + 1):
s[i] = s[i - 1] + nums[i - 1]
for i in range(1, n + 1):
preMin[i] = min(preMin[i - 1], s[i])
for i in range(1, n + 1):
ans = max(ans, s[i] - preMin[i - 1])
return ans
1.3.3 304 . 二维区域和检索 - 矩阵不可变
- 思路; 此类题目牢记以下公式即可
前缀和数组: S [ i ] [ j ] = ∑ x = 1 i ∑ y = 1 j A [ x ] [ y ] = S [ i ? 1 ] [ j ] + S [ i ] [ j ? 1 ] ? S [ i ? 1 ] [ j ? 1 ] + A [ i ] [ j ] S[i][j]=\sum_{x=1}^{i} \sum_{y=1}^{j} A[x][y]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+A[i][j] S[i][j]=∑x=1i?∑y=1j?A[x][y]=S[i?1][j]+S[i][j?1]?S[i?1][j?1]+A[i][j]
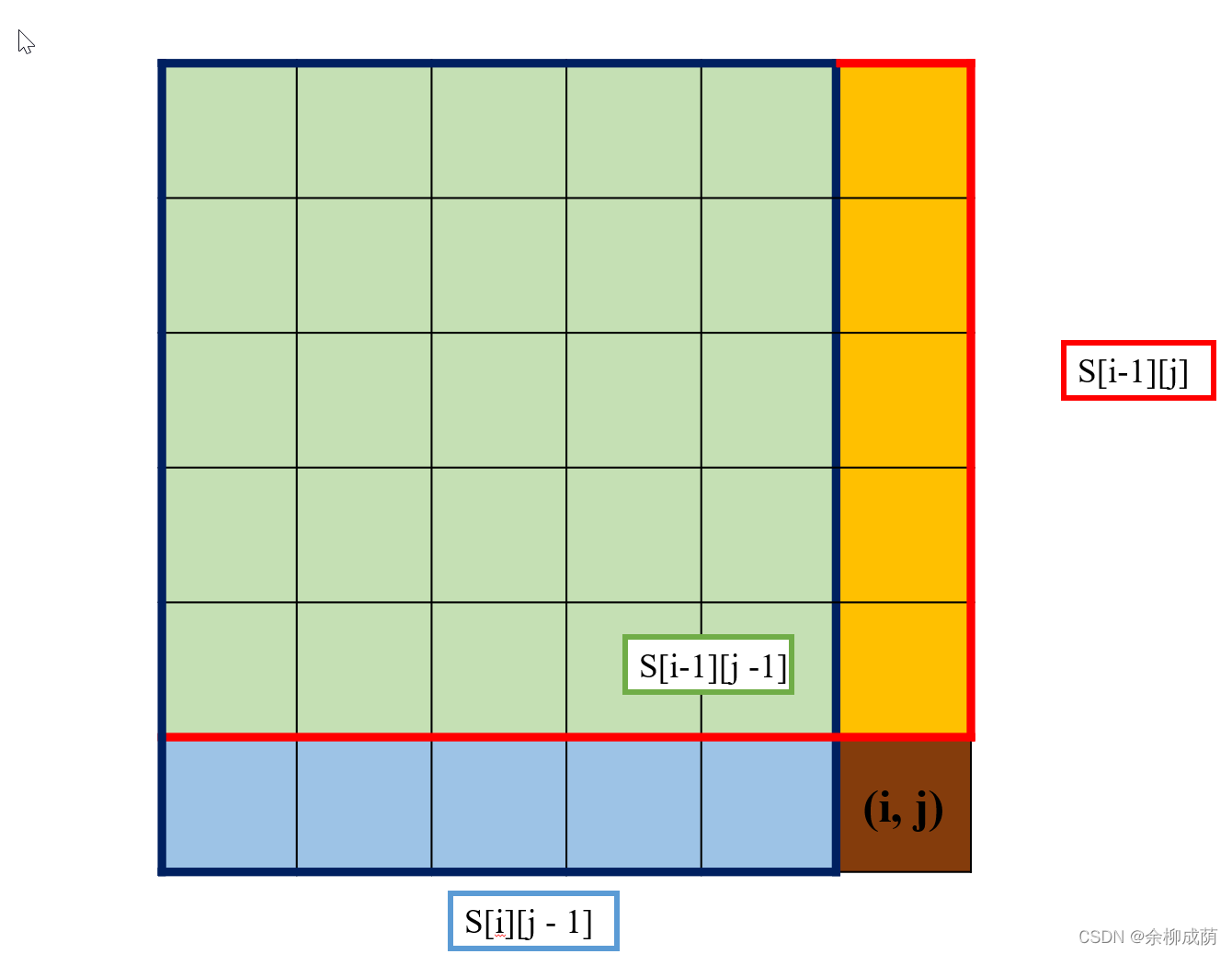
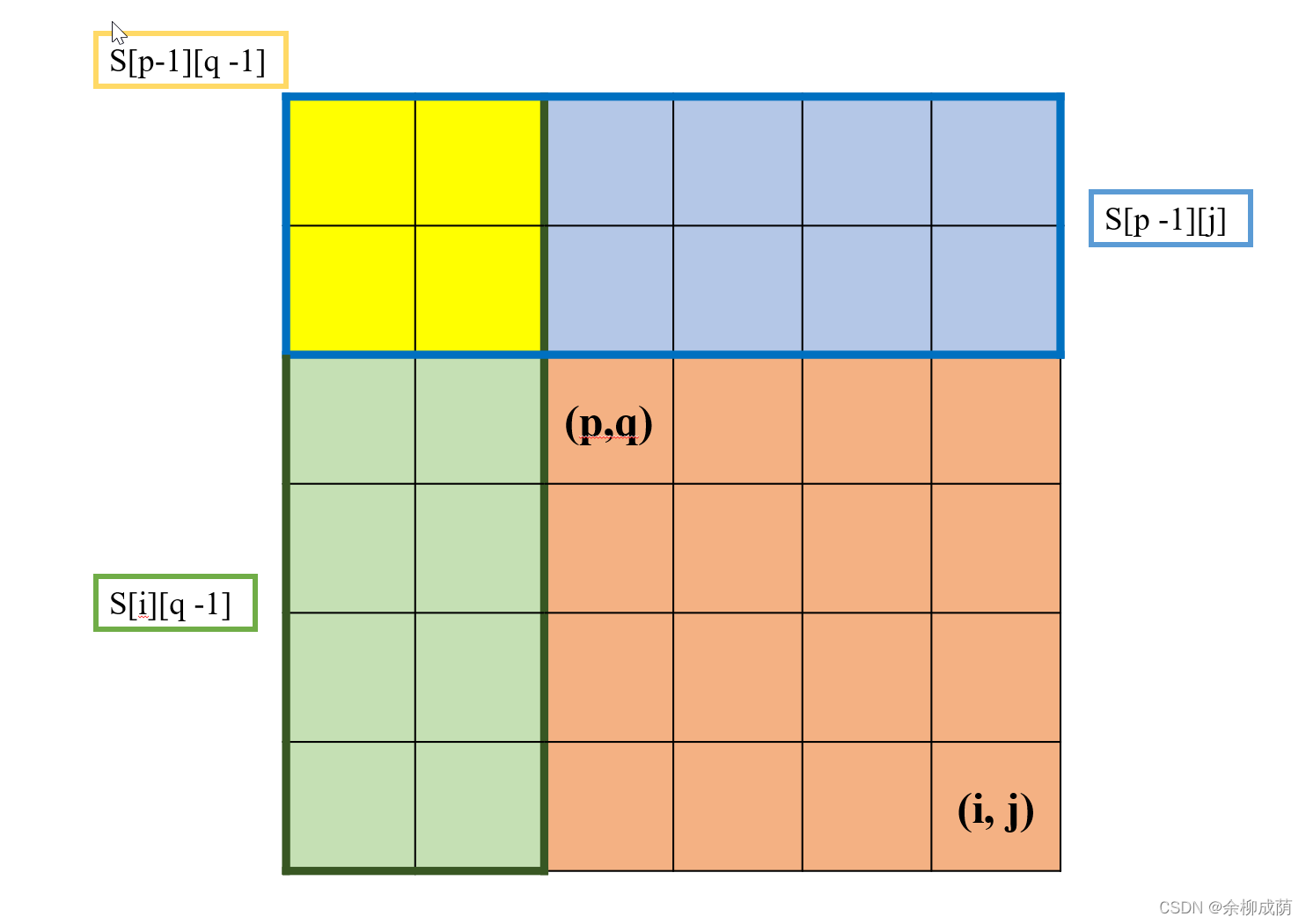
子矩阵和: sum ? ( p , q , i , j ) = ∑ x = p i ∑ y = q j A [ x ] [ y ] = S [ i ] [ j ] ? S [ i ] [ q ? 1 ] ? S [ p ? 1 ] [ j ] + S [ p ? 1 ] [ q ? 1 ] \operatorname{sum}(p, q, i, j)=\sum_{x=p}^{i} \sum_{y=q}^{j} A[x][y]=S[i][j]-S[i][q-1]-S[p-1][j]+S[p-1][q-1] sum(p,q,i,j)=∑x=pi?∑y=qj?A[x][y]=S[i][j]?S[i][q?1]?S[p?1][j]+S[p?1][q?1]
图中红色为所求子矩阵:
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
r = len(matrix)
l = len(matrix[0])
self.s = [[0] * (l + 1) for _ in range(r + 1)]
for i in range(1, r + 1):
for j in range(1, l + 1):
self.s[i][j] = self.s[i-1][j] + self.s[i][j-1] - self.s[i-1][j-1] + matrix[i - 1][j - 1]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
return self.s[row2 + 1][col2 + 1] - self.s[row2 + 1][col1] - self.s[row1][col2 + 1] + self.s[row1][col1]
2 差分
2.1 基本思想
差分可以简单的看成序列中每个元素与其前一个元素的差
-
如图B为A的差分数组: B 1 = A 1 , B i = A i ? A i ? 1 ( 2 ≤ i ≤ n ) B_{1}=A_{1}, B_{i}=A_{i}-A_{i-1}(2 \leq i \leq n) B1?=A1?,Bi?=Ai??Ai?1?(2≤i≤n) . 可见对其求前缀和 >>>> 获得数组A
- 于是 >>>> 差分是前缀和的逆操作
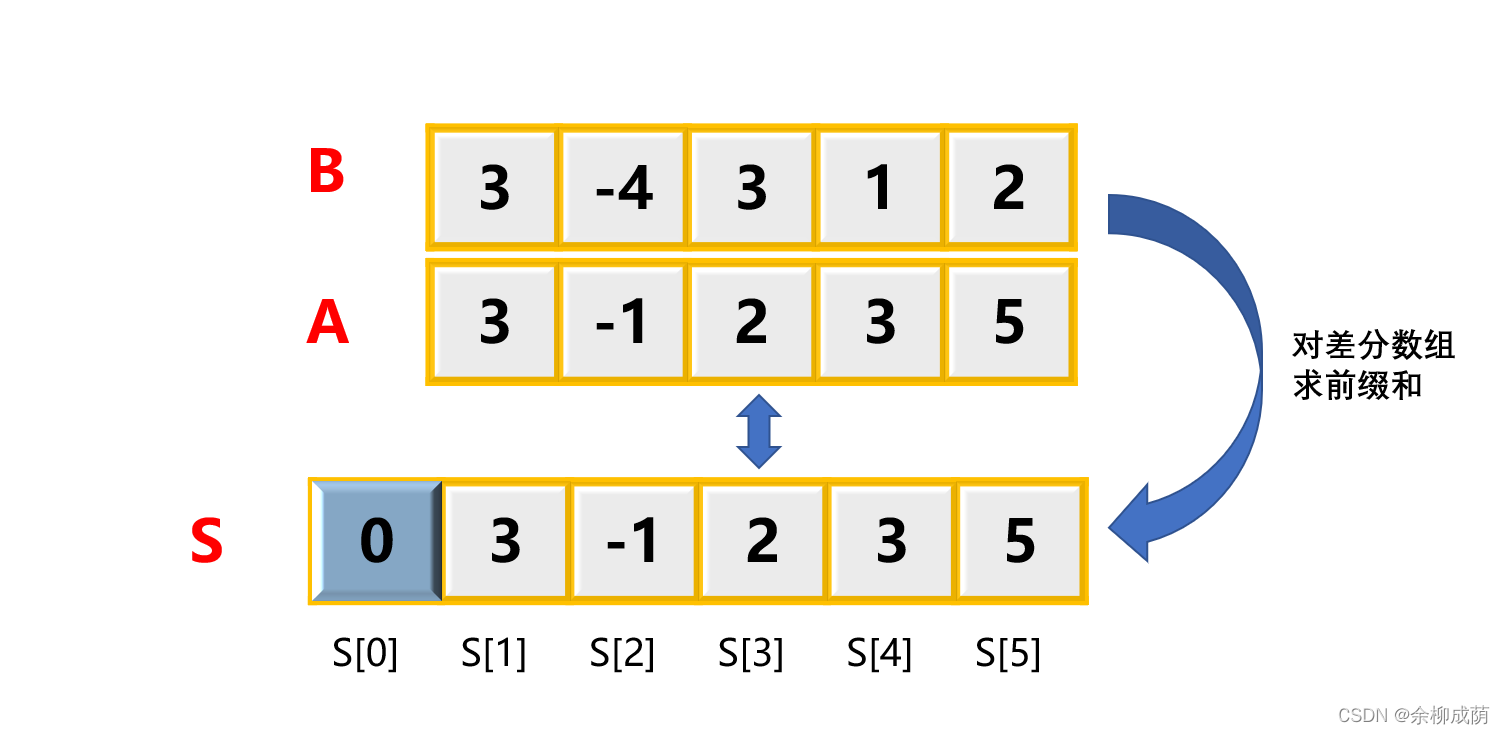
- 于是 >>>> 差分是前缀和的逆操作
-
差分操作目的:
- 在对长度为n的数组操作m次时, 每次操作需对 l 到 r 个元素加/减去常数 1: A l A_l Al? + 1, A l + 1 + 1 A_{l+1} +1 Al+1?+1 … A r A_r Ar? + 1, → 需要对 l →r 所有元素操作
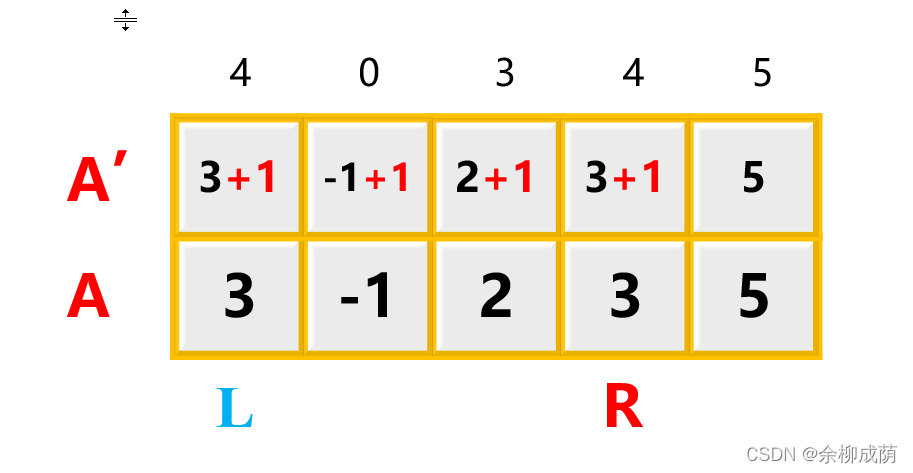
- 改为对差分数组B操作: 仅需 B l B_l Bl? + 1 以及 B r + 1 ? 1 B_{r+1} -1 Br+1??1 操作即可 >>> 再对B求前缀和获得改变后的A
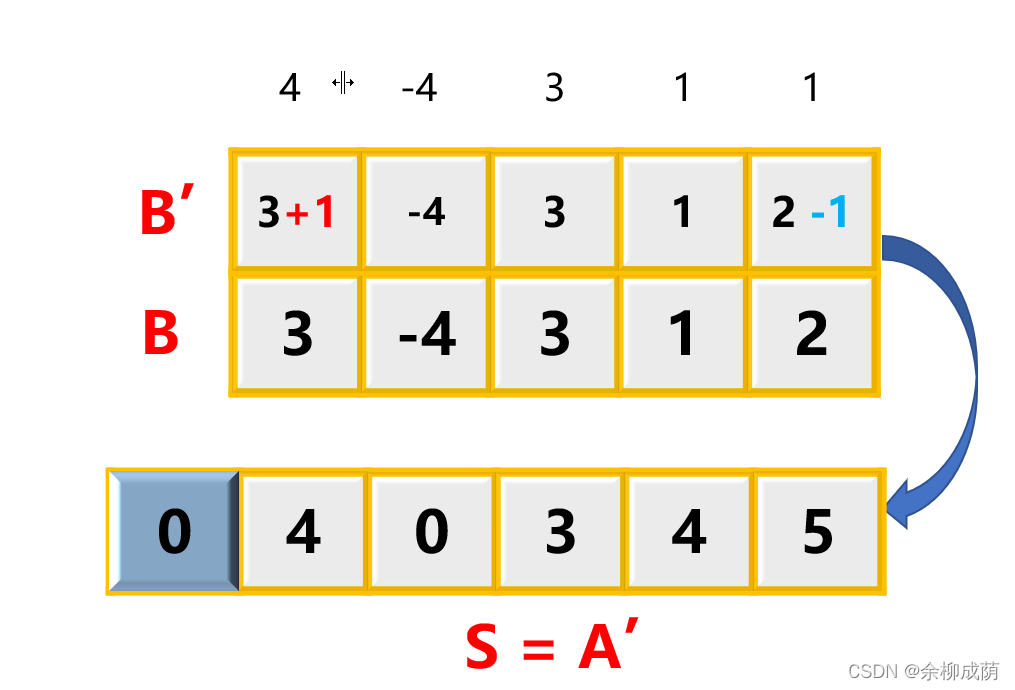
2.2 相关例题
2.2.1 1109 . 航班预订统计
- 思路: 对原
first → last操作 >>> 对其差分数组操作, 再还原
class Solution:
def corpFlightBookings(self, bookings: List[List[int]], n: int) -> List[int]:
ans = [0] * (n + 1) # 后多一个0
for booking in bookings:
first = booking[0]
last = booking[1]
seat = booking[2]
ans[first - 1] += seat
ans[last] -= seat
s = [0] * (n + 1) # 前多一个0
for i in range(1, n + 1):
s[i] = s[i - 1] + ans[i - 1]
return s[1:]
3 双指针
3.1 基本思想
双指针(Two Pointers):指的是在遍历元素的过程中,不是使用单个指针进行访问,而是使用两个指针进行访问,从而达到相应的目的。如果两个指针方向相反,则称为「对撞时针」。如果两个指针方向相同,则称为「快慢指针」。如果两个指针分别属于不同的数组 / 链表,则称为「分离双指针」。
- 数组问题时间复杂度通常为 O ( n 2 ) O(n^2) O(n2) ---- 利用区间单调性 >>>>转化为O(n)
对撞指针:指的是两个指针
left、right分别指向序列第一个元素和最后一个元素,然后left指针不断递增,right不断递减,直到两个指针的值相撞(即left == right),或者满足其他要求的特殊条件为止。
步骤:
(1) 两个指针 left,right, left指向第一个元素. right指向最后一个元素;
(2)相互靠近: left += 1, right -= 1
(3)相撞: left == right 或其他条件跳出条件
- 一般用来解决有序数组或者字符串问题
快慢指针:指的是两个指针从同一侧开始遍历序列,且移动的步长一个快一个慢。移动快的指针被称为 「快指针(fast)」,移动慢的指针被称为「慢指针(slow)」。两个指针以不同速度、不同策略移动,直到快指针移动到数组尾端,或者两指针相交,或者满足其他特殊条件时为止。
-
步骤
(1) 两个指针slow、fast, 一般slow = 0,fast = 1
(2)两个指针分别满足条件移动
(3)快指针到头或其他条件跳出 -
一般用于处理数组中的移动、删除元素问题,或者链表中的判断是否有环、长度问题
分离双指针:两个指针分别属于不同的数组 / 链表,两个指针分别在两个数组 / 链表中移动。
-
步骤
(1)两个指针left_1、left_2, 分别指向两个数组, 链表的首个元素
(2)满足条件left_1、left_2同时右移, 或只移动其中一个
(3)其中一个数组或链表遍历完 或者 其他条件满足跳出 -
一般用于处理有序数组合并,求交集、并集问题
3.2 相关例题
3.2.1 11. 盛最多水的容器 - 力扣(LeetCode)
- 思路 : 积水量 = 左右较小高度 * 宽度 >>>> 宽度随着左右移动递减, 高度两者较小者越大则面积越大 >>>>>> 左右哪一个更小则向内部移动(其对应最大面积已求出)
class Solution:
def maxArea(self, height: List[int]) -> int:
l, r, ans = 0, len(height) - 1, 0
while l < r:
ans = max(ans, min(height[l], height[r]) * (r - l))
if height[l] < height[r]:
l += 1
else:
r -= 1
return ans
3.2.2 167 . 两数之和 II - 输入有序数组
- 思路: 有序数组 >>> 两头相加, 小于
target左指针右移 使和增大; 大于target右指针左移, 使和减小
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left, right = 0, len(numbers) - 1
while left <= right:
sum_num = numbers[left] + numbers[right]
if sum_num == target:
return [left + 1, right + 1]
elif sum_num < target:
left += 1
else:
right -= 1
3.2.3 15 . 三数之和
- 思路: 先对数组排序, 遍历数组得
num[ i ]>>> 使得a + b = - num[i]既满足条件 >>> 再考虑相等元素输出重复问题 → 等价于 用i遍历数组过程 嵌套一个 两数之和问题
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
ans, n = [], len(nums)
for i in range(n):
if i > 0 and nums[i] == nums[i - 1]: #去重
continue
right = n - 1
for left in range(i + 1, n - 1):
if left > i + 1 and nums[left] == nums[left - 1]:
continue
while left < right and nums[left] + nums[right] > -nums[i]:
right -= 1
if left < right and nums[left] + nums[right] == -nums[i]:
ans.append([nums[i],nums[left],nums[right]])
return ans
4 递归
4.1 基本思想
递归(recursion):程序调用自身的编程技巧。
-
递归满足2个条件:
1)有反复执行的过程(调用自身) --------- 类似
a[n] = a[n - 1]过程2)有跳出反复执行过程的条件(递归出口)
-
递归的三个关键:
? 定义需要递归的问题(重叠子问题) ---- 数学归纳法思维
? 确定递归边界
? 保护与还原现场
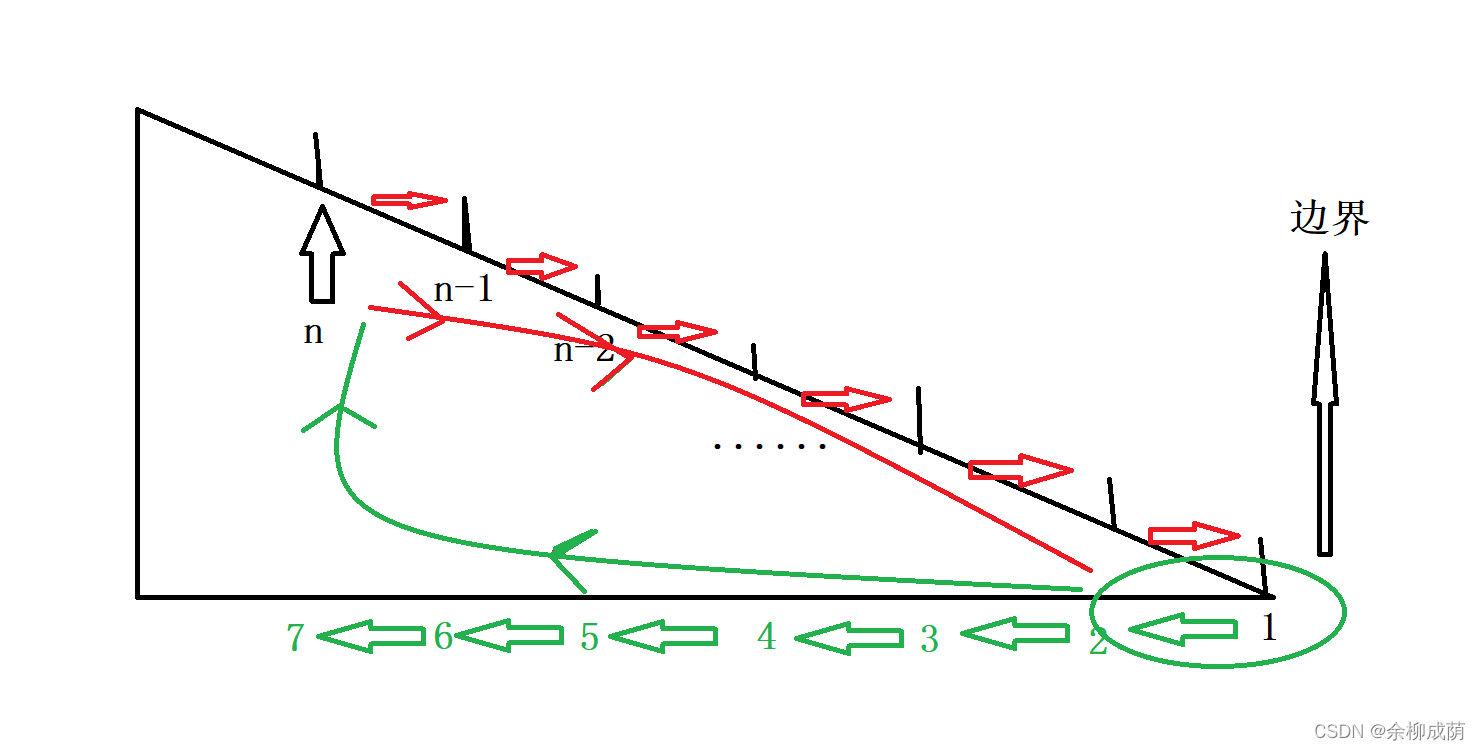
-
复杂的问题,每次都解决一点点,并将剩下的任务转化成为更简单的问题等待下次求解,如此反复,直到最简单的形式
-
python模板
def recursion(level, param1, param2,...):
# recursion terminator
if level > MAX_LEVEL:
#process result
return
# process logic in current level
process(level, data...)
# drill down
self.recursion(level + 1,new_param1,...)
# restore the current level status if needed
4.2 相关题目
4.2.1 78 . 子集
- 思路: 递归 -----
优雅 - 法一考虑从第一个元素到最后一个元素 >>> 有选择进入子集或不进入子集(nums[i]是否选择) 两种情况 >>> 利用公共空间储存子集, 节省空间, 设置边界 -----
i = n时 令选择公共数组加入答案数组
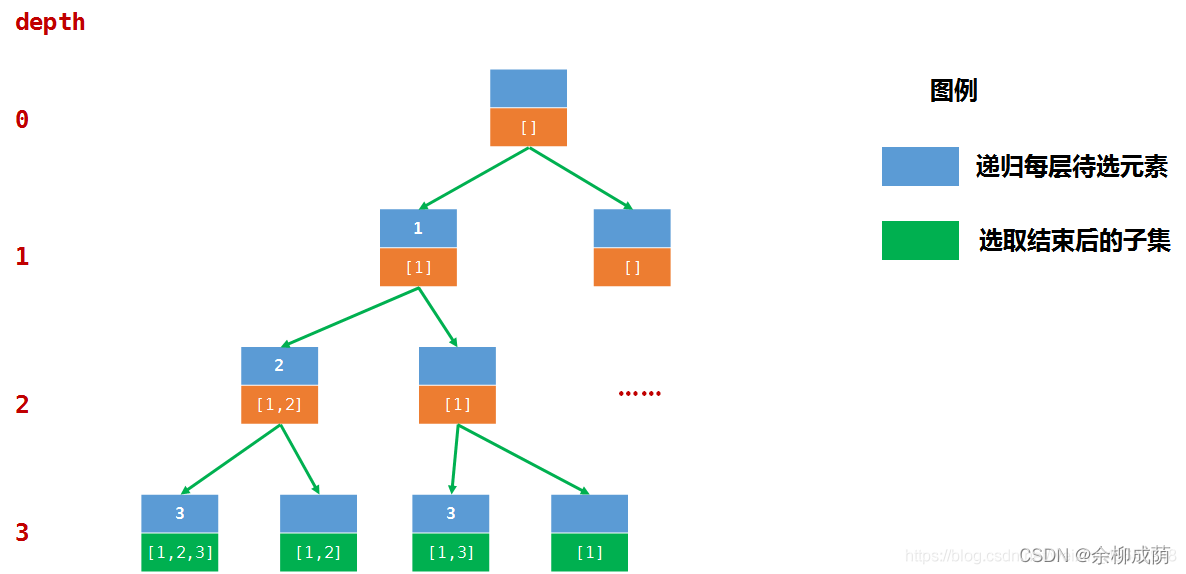
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n, choose, ans = len(nums), [], []
def recur(i):
if i == n: # 边界达成, 功成身退
ans.append(choose[:])
return
recur(i + 1) # 不选择nums[i], 直接下一循环
choose.append(nums[i]) #选择, 加入nums[i]进入临时公共表
recur(i + 1)
choose.pop() # 还原现场
recur(0)
return ans
-
- 注意: 老问题 :
ans.append(choose[:])加入的是choose[:]创建副本, 而非choose, 改变choose的值并不会影响已经添加到 ans 的部分; 若是直接将choose添加到 ans 中,这里choose还是指向同个内存地址,由于后续递归会改变choose的值,那么最终 ans 里面部分相关的内容都会改变 >>> 变成全为空 –[]
- 注意: 老问题 :
- 思路二 ---- 同样递归 -------
for(从i开始)里面 嵌套recur(j + 1)来去除非子集
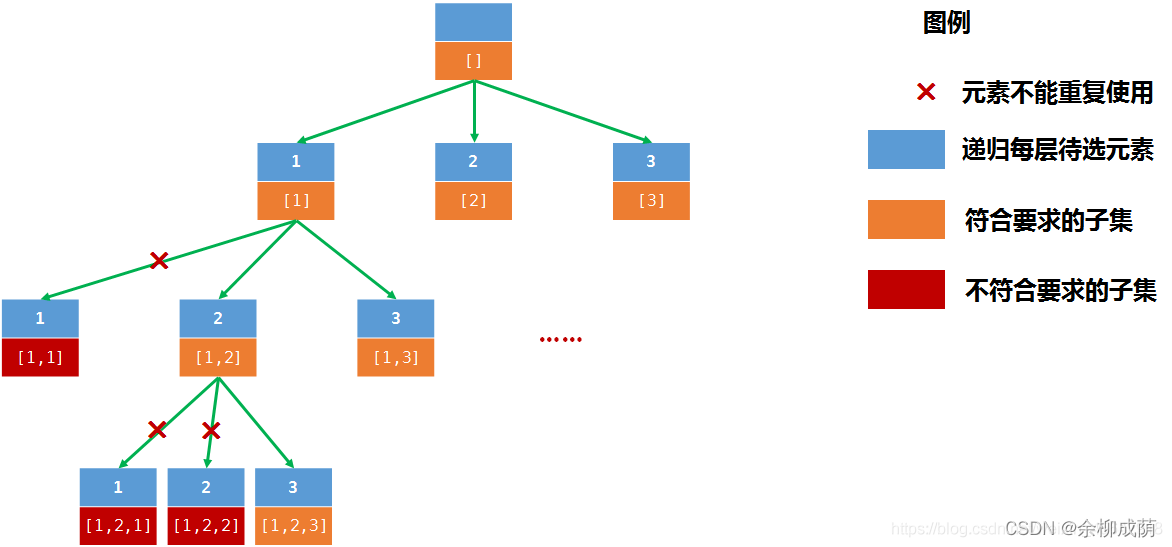
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n, choose, ans = len(nums), [], []
def recur(i):
ans.append(choose[:])
for j in range(i, n):
choose.append(nums[j])
recur(j + 1) # 避免重复,每次递归,从下一个索引开始
choose.pop()
recur(0)
return ans
4.2.2 77 . 组合
- 思路: 以上子集的思路一 增加条件筛选(增加的数组长度为k)即可 ------
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
choose, ans = [], []
def recur(i):
if i == n + 1 :
if len(choose) == k: #条件
ans.append(choose[:])
return
recur(i + 1)
choose.append(i)
recur(i + 1)
choose.pop() # 还原现场
recur(1)
return ans
- 优化 ----- 剪枝 ---- 提前筛选去除不合题意方案 >>>>>
choose[:]长度超过k个 或者 在剩下(n - k + 1)个与choose[:]长度之和都小于k >>>>提前退出 → 快了一个数量级 : 操作数由 2 n 2^n 2n 变为 C n k C_{n}^{k} Cnk?
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
choose, ans = [], []
def recur(i):
if len(choose) > k or len(choose) + (n - i + 1) < k: #剪枝
return
if i == n + 1 :
ans.append(choose[:])
return
recur(i + 1)
choose.append(i)
recur(i + 1)
choose.pop() # 还原现场
recur(1)
return ans

4.2.3 46 . 全排列
- 思路一: 与以上递归大致类似, 利用
[False] * n数组来验证choose每一个位置是否存有元素
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
n, choose, ans, bool_i = len(nums), [], [], [False] * len(nums)
def recur(index):
if index == n:
ans.append(choose[:])
return
for i in range(n):
if bool_i[i] == False:
choose.append(nums[i])
bool_i[i] = True
recur(index + 1)
bool_i[i] = False
choose.pop()
recur(0)
return ans
- 思路二 题解p神解法 — 同样递归, 但递归的是不断缩小
nums[]区间 ------- 十分优雅
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
ans = []
def recur(nums, choose):
if not nums:
ans.append(choose) #当选完, nums为空, 结束
return
for i in range(len(nums)):
recur(nums[:i] + nums[i+1:], choose + [nums[i]]) # 在除了nums[i]剩余元素找数字
recur(nums, [])
return ans
4.3 递归基本形式总结
- 以上三个问题都是递归实现的"暴力搜索"(或者叫枚举、回溯等) 可以总结为以下三种基本形式
| 递归形式 | 时间复杂度规模 | 问题举例 |
|---|---|---|
| 指数型 | k n k^n kn | 子集、大体积背包 |
| 排列型 | n ! n! n! | 全排列、旅行商、N皇后 |
| 组合型 | n ! m \ ( n ? m ) ! \frac{\mathrm{n} !}{m \backslash(n-m) !} m\(n?m)!n!? | 组合选数 |
4.4 树相关题目:
4.4.1 226 . 翻转二叉树
- 思路 递归翻转每一层
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root: #节点为空时返回
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
4.4.2 98 . 验证二叉搜索树
- 思路: 递归 + 限制左右子节点的范围 >>>> 从首个节点A[0]范围(
[min, max])开始, 左子节点范围[min, A[0] - 1], 右子节点范围[A[0] + 1, max]
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def check(self, root, min_range, max_range):
if not root:
return True
if root.val < min_range or root.val > max_range:
return False
return check(self, root.left, min_range, root.val - 1) and check(self, root.right, root.val + 1, max_range)
return check(self, root,-(1<<31), (1<<31) -1)
5 分治
5.1 基本思想
分治(Divide-and-Conquer): 即"分而治之"就是把原问题划分成若干个同类子问题,分别解决后,再把结果合并起来
-
关键点:
- 原问题和各个子问题都是重复的(同类的)一递归定义
- 除了向下递归"问题",还要向上合并"结果〃
分治算法一般用递归实现
-
分治算法的"递归状态树"
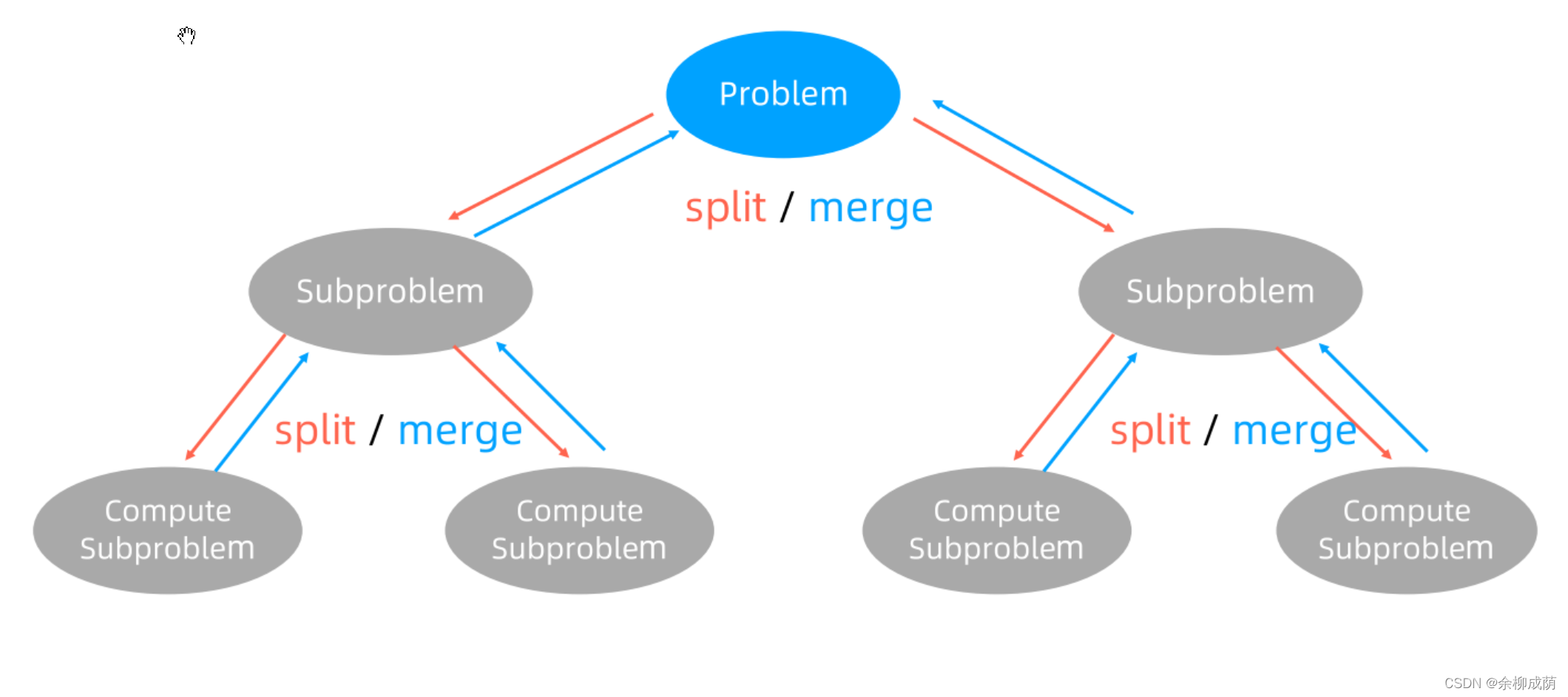
5.2 相关题目
5.2.1 50 . Pow(x, n)
- 思路:
x
n
x^n
xn 问题分为 >>>
x
n
/
2
x^{n/2}
xn/2 *
x
n
/
2
x^{n/2}
xn/2 的问题 >>> 特殊地: n为奇数, 由于
n/2向下取整 结果多乘x ; n为负数, 结果= 1/(x^-n)
class Solution:
def myPow(self, x: float, n: int) -> float:
if n == 0:
return 1 #边界
if n < 0:
return 1.0 / self.myPow(x, -n)
temp = self.myPow(x, n//2)
ans = temp * temp
if n % 2 == 1:
ans *= x
return ans
5.2.3 22 . 括号生成
- 思路: 按断点分括号有拆分 >>>> 以 加法 + 乘法形式来分割括号组(通式):
(A) B的形式,A,B表示若干个合法括号组合 >>>> 不重不漏
如实例一 :
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
- 可以看做: (A)B 形式 : A有
k - 1对合法括号,k>=1, 则B表示n - k对合法括号:k = 1>>>>>(A)为(); 则n - k = 2>>>>>B为()()(())---->>>()()()()(())k = 2>>>>>(A)为(()); 则n - k = 1>>>>>B为()---->>>(())()k = 3>>>>>(A)为((()))(()()); 则n - k =0>>>>>B为---->>>((()))(()())
五种情况不多不少
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
ans = []
if n == 0:return [""]
for k in range(1, n + 1):
A = self.generateParenthesis(k - 1)
B = self.generateParenthesis(n - k)
for a in A:
for b in B:
ans.append("(" + a + ")" + b)
return ans
6 课后作业
6.1 47 . 全排列 II
- 思路1 ---- 直接在原全排列边界处加一条件 : 判断是否出现过即可 ----- 直接加了一个数量级复杂度, 太慢
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
ans = []
def recur(nums, choose):
if not nums:
if choose not in ans: # 判断是否出现过
ans.append(choose)
return
for i in range(len(nums)):
recur(nums[:i] + nums[i+1:], choose + [nums[i]]) # 在除了nums[i]剩余元素找数字
recur(nums, [])
return ans
- 思路二 排序后利用
nums[ i ] == nums[i - 1]剪枝
考虑重复元素一定要优先排序,将重复的都放在一起,便于找到重复元素和剪枝!
推广至 --> 如果涉及考虑重复元素,或者大小比较的情况,对列表排序是一个不错的选择
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
ans = []
def recur(nums, choose):
if not nums:
ans.append(choose)
return
for i in range(len(nums)):
if i > 0 and nums[i] == nums[i - 1]:
continue
recur(nums[:i] + nums[i+1:], choose + [nums[i]]) # 在除了nums[i]剩余元素找数字
nums.sort()
recur(nums, [])
return ans

6.2 23 . 合并K个升序链表
- 思路: 将多个链表问题分解 >>> 链表两两合并问题>>> 两个递归解决: 1是 21 . 合并两个有序链表的两个链表(L1,L2)合并; 2 是类似二分法的将
LIst分成若干个L1, L2
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
if not lists:return
return self.merge(lists, 0, len(lists) - 1)
def merge(self, lists, left, right):
if left == right: #边界
return lists[left]
mid = left + (right - left) // 2 # 向下取整
l1 = self.merge(lists, left, mid)
l2 = self.merge(lists,mid + 1, right)
return self.mergeTwoLists(l1, l2)
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode: # L1与L2合并
if not l1: return l2 # 终止条件,直到两个链表都空
if not l2: return l1
if l1.val <= l2.val: # 递归调用
l1.next = self.mergeTwoLists(l1.next,l2)
return l1
else:
l2.next = self.mergeTwoLists(l1,l2.next)
return l2
参考资料
- https://zhuanlan.zhihu.com/p/117569086 【朝夕的ACM笔记】算法基础-前缀和
- https://www.jianshu.com/p/89ec2814682c 前缀和 (差分)算法
- https://www.cnblogs.com/kyoner/p/11087755.html 双指针技巧汇总
- https://algo.itcharge.cn/ 算法通关手册(LeetCode)
- https://www.freesion.com/article/9741469809/递归算法入门
- https://time.geekbang.org/column/article/73511?utm_source=u_nav_web&utm_medium=u_nav_web&utm_term=u_nav_web递归(上):泛化数学归纳,如何将复杂问题简单化?
- https://zhuanlan.zhihu.com/p/72734354经典算法思想2——分治(Divide-and-Conquer)