前言?

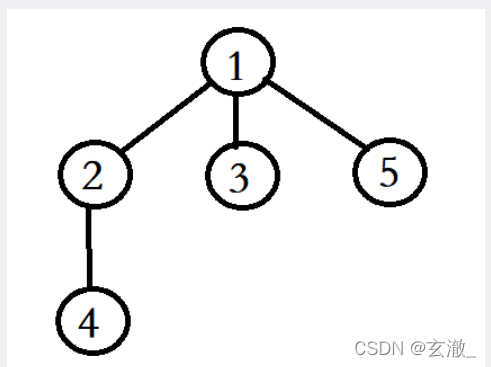
在上一章的内容中我们使用了深度优先搜索来进行遍历，这一章我们选择使用广度优先搜索来完成这个图的遍历 --> 结果如下:

广度优先搜索过程

使用广度优先搜索来遍历这个图的过程如下。

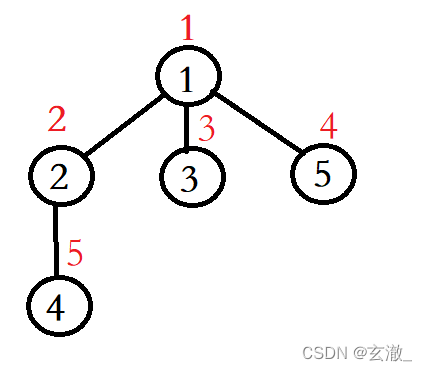
首先以一个未被访问过的顶点作为起始顶点，比如以1号点作为起始顶点。

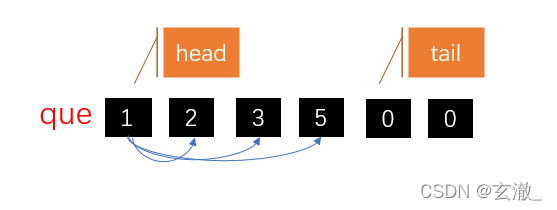
将1号点放到队列中，然后将与1号点相邻的未访问过的顶点即 2,3,5号顶点依次放入队列中，如下图：

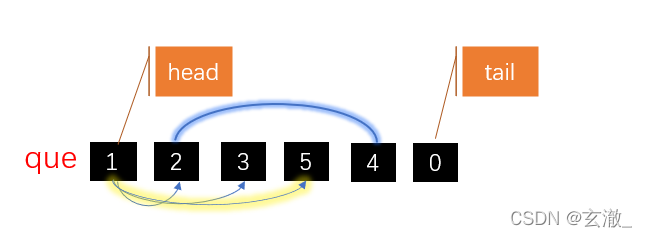
接下来将2号顶点相邻的未访问过的顶点4号放入到队列中。到此所有的顶点都访问过了，遍历结束。如下图：

主要思想?

首先以一个未被访问过的顶点作为起始顶点，访问其所有相邻的点

然后对每个相邻的的点，再访问他们相邻的未被访问过的顶点，直到所有的顶点都被访问过，遍历结束。

代码实现?

#include <stdio.h>
int main()
{
    int i, j, m, a, b, cur,n, book[101] = { 0 }, e[101][101];
    int que[10001], head, tail;
    scanf("%d %d", &n, &m);
    //初始化二维矩阵
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            if (i == j) e[i][j] = 0;
            else e[i][j] = 99999999;	//我们假设99999999为x

    //读入顶点之间的边
    for (i = 1; i <= n; i++)
    {
        scanf("%d %d", &a, &b);
        e[a][b] = 1;
        e[b][a] = 1;	//因为该图为无向图
    }

    //队列初始化
    head = 1;
    tail = 1;

    //从1号顶点出发，将1号顶点加入队列
    que[tail] = 1;
    tail++;
    book[1] = 1;//标记1号顶点已经入列

    //当队列不为空时循环
    while (head < tail && tail <= n)
    {
        cur = que[head];  //当前正在访问的顶点编号
        for (i = 1; i <= n; i++)
        {
            //判断从顶点cur到顶点i是否有边，并判断顶点i是否访问过
            if (e[cur][i] == 1 && book[i] == 0)
            {
                //如果从顶点cur到顶点i右边，且顶点i没有被访问过，将顶点i入列
                que[tail] = i;
                tail++;
                book[i] = 1; //标记表示已经访问过

            }
            if (tail > n)  //表示所有点都已经访问过
                break;
        }

        head++;
        //注意这个地方，不要忘记head++后，才能继续向下拓展
    }

    for (i = 1; i < tail; i++)
        printf("%d",que[i]);


}