一、数组
特点:
- 内存地址连续
- 可以通过下标的成员访问,下标访问的性能高
- 增删操作带来更大的性能消耗(保证数据越界的问题,需动态扩容)
数组增删操作 ——> 新创建数组 ——> 给新数组赋值 ——> 性能消耗
二、链表
单向链表和双向链表
双向链表

如上图,定义了五个结点。
prev 代表当前节点的前一节点地址
next代表当前节点的下一节点地址
双向链表的节点是首尾相连的,可以通过当前节点可以方便的找到上一节点和下一节点
特点:
- 灵活的空间要求,存储空间不要求连续
- 不支持下标访问,支持顺序的遍历检索
- 针对增删操作找到对应的节点改变链表的头尾执行即可,无序移动元素存储位置
添加节点

删除节点

LinkedList 底层源码
private static class Node<E> {
E item; //节点的元素
Node<E> next; //下一节点
Node<E> prev; //上一节点
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
三、树
3.1 二叉树

添加的第一个元素是根节点。比根节点小添加到左边,比根节点大添加到右边,依此类推到子节点。
二叉树具有如下的特点
- 某节点的左子树节点值仅包含小于该节点值
- 某节点的右子树节点值仅包含大于该节点值
- 左右子树每个也必须是二叉查找树
- 顺序排列

查询效率不高,
面对这个问题我们可以参考在高中学习生物时学过一个关键字去除顶端优势,通过去除植物顶端优势,侧芽会迅速生长,慢慢变得强壮和平衡, 红黑树其实就是去除二叉查找树顶端优势的解决方案,从而达到树的平衡
3.2红黑树
红黑树,Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST),树上的每个节点都遵循下面的规则:
- 性质1:每个节点要么是黑色,要么是红色。
- 性质2:根节点是黑色。
- 性质3:每个叶子节点(NIL)是黑色。
- 性质4:每个红色结点的两个子结点一定都是黑色。
- 性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
黑平衡二叉树
recolor (重新标记黑色或红色)
rotation (旋转,这是树达到平衡的关键)
节点描述约定

红黑树能自平衡,它靠的是什么?三种操作:左旋、右旋和变色
? 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
? 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
? 变色:结点的颜色由红变黑或由黑变红。
插入处理的场景

插入情景1:红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行,但注意,根据红黑树性质2:根节点是黑色。还需要把插入结点设为黑色。
处理:把插入结点作为根结点,并把结点设置为黑色。
插入情景2:插入结点的父结点为黑结点
由于插入的结点是红色的,当插入结点的黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
处理:直接插入。
插入情景3:插入结点的父结点为红结点
再次回想下红黑树的性质2:根结点是黑色。如果插入的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。这点很重要,因为后续的旋转操作肯定需要祖父结点的参与。
情景3又分为很多子情景,下面进入重点部分
插入情景3.1:叔叔结点存在并且为红结点
从红黑树性质4可以,祖父结点肯定为黑结点,因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红。


插入情景3.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
单纯从插入前来看,也即不算情景3.1自底向上处理时的情况,叔叔结点非红即为叶子结点(Nil)。因为如果叔叔结点为黑结点,而父结点为红结点,那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了,这不满足红黑树的性质5。后续情景同样如此,不再多做说明了。
前文说了,需要旋转操作时,肯定一边子树的结点多了或少了,需要租或借给另一边。插入显然是多的情况,那么把多的结点租给另一边子树就可以了。
插入情景3.2.1:插入结点是其父结点的左子结点

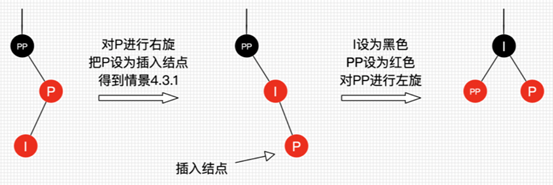
插入情景3.2.2:插入结点是其父结点的右子结点
这种情景显然可以转换为情景3.2.1

插入情景3.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
该情景对应情景3.2,只是方向反转,不做过多说明了,直接看图