1 简介
基于改进粒子群算法的移动机器人路径规划,通过建立目标函数,变换坐标等对环境建模,再引入反向粒子群优化算法,得到全局最优路径.MATLAB仿真结果显示,此方法可有效地解决空间作业机器人路径规划及避障问题.与传统粒子群算法比,该法建模容易,计算快捷,可以在不同的障碍物环境下得到不同的优化轨迹?。

2 部分代码
clc;
close all
clear
load('data4.mat')
S=(S_coo(2)-0.5)*num_shange+(S_coo(1)+0.5);%起点对应的编号
E=(E_coo(2)-0.5)*num_shange+(E_coo(1)+0.5);%终点对应的编号
PopSize=20;%种群大小
OldBestFitness=0;%旧的最优适应度值
gen=0;%迭代次数
maxgen =200;%最大迭代次数
c1=0.5;%认知系数
c2=0.7;%社会学习系数
c3=0.2;%反向因子
w=0.96;%惯性系数
%%
%初始化路径
w_min=0.5;
w_max=1;
Group=ones(num_point,PopSize);? %种群初始化
flag=1;
%% 初始化粒子群位置
for i=1:PopSize
? ? p_lin=randperm(num_point)';%随机生成1*400不重复的行向量
? ? ?%% 将起点编号放在首位
? ? ? ? index=find(p_lin==S);
? ? ? ? lin=p_lin(1);
? ? ? ? p_lin(1)=p_lin(index);
? ? ? ? p_lin(index)=lin;
? ? ? ? Group(:,i)=p_lin;
? ? ? ? %%将每个个体进行合理化处理
? ? ? ? [Group(:,i),flag]=deal_fun(Group(:,i),num_point,liantong_point,E,num_shange);
? ? ? ? ?fangxiang_Group(:,i)=fangxiang(Group(:,i),c3);%方向粒子数量
? ? while flag==1%如处理不成功,则初始化个体,重新处理
? ? ? ? %% 将起点编号放在首位
? ? ? ? index=find(p_lin==S);
? ? ? ? lin=p_lin(1);
? ? ? ? p_lin(1)=p_lin(index);
? ? ? ? p_lin(index)=lin;
? ? ? ? Group(:,i)=p_lin;
? ? ? ? fangxiang_Group(:,i)=p_lin;
? ? ? ? %%将每个个体进行合理化处理
? ? ? ? [Group(:,i),flag]=deal_fun(Group(:,i),num_point,liantong_point,E,num_shange);
? ? ? ? ?[fangxiang_Group(:,i),flag]=deal_fun(fangxiang_Group(:,i),num_point,liantong_point,E,num_shange);
? ? end
? ?
end
%最优解
figure(3)
hold on
for i=1:num_shange
? ? for j=1:num_shange
? ? ? ? if sign(i,j)==1
? ? ? ? ? ? y=[i-1,i-1,i,i];
? ? ? ? ? ? x=[j-1,j,j,j-1];
? ? ? ? ? ? h=fill(x,y,'k');
? ? ? ? ? ? set(h,'facealpha',0.5)
? ? ? ? end
? ? ? ? s=(num2str((i-1)*num_shange+j));
? ? ? ? text(j-0.95,i-0.5,s,'fontsize',6)
? ? end
end
axis([0 num_shange 0 num_shange])%限制图的边界
plot(S_coo(2),S_coo(1), 'p','markersize', 10,'markerfacecolor','b','MarkerEdgeColor', 'm')%画起点
plot(E_coo(2),E_coo(1),'o','markersize', 10,'markerfacecolor','g','MarkerEdgeColor', 'c')%画终点
set(gca,'YDir','reverse');%图像翻转
for i=1:num_shange
? ? plot([0 num_shange],[i-1 i-1],'k-');
? ? plot([i i],[0 num_shange],'k-');%画网格线
end
for i=2:index1
? ? Q1=[mod(route_lin(i-1)-1,num_shange)+1-0.5,ceil(route_lin(i-1)/num_shange)-0.5];
? ? Q2=[mod(route_lin(i)-1,num_shange)+1-0.5,ceil(route_lin(i)/num_shange)-0.5];
? ? plot([Q1(1),Q2(1)],[Q1(2),Q2(2)],'r','LineWidth',3)
end
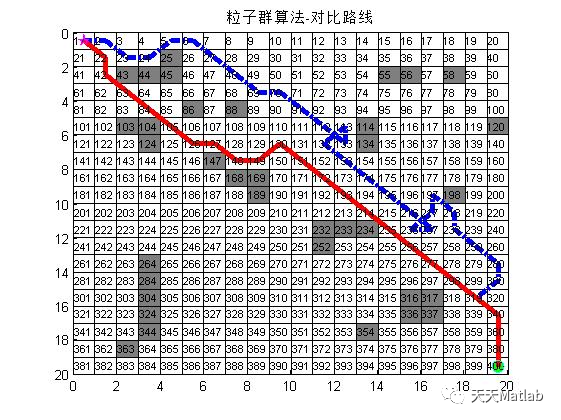
title('改进后的粒子群算法-最优路线');
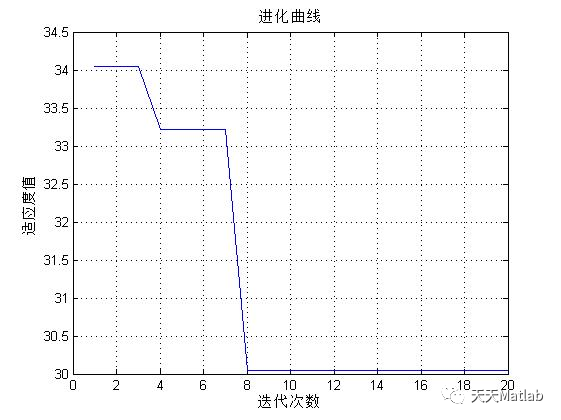
%进化曲线
figure(4);
plot(BestFitness);
xlabel('迭代次数')
ylabel('适应度值')
grid on;
title('改进后的进化曲线');
disp('改进后的粒子群算法-最优路线方案:')
disp(num2str(route_lin))
disp(['起点到终点的距离:',num2str(BestFitness(end))]);
figure(5);
plot(BestFitness*100);
xlabel('迭代次数')
ylabel('适应度值')
grid on;
title('改进后的最佳个体适应度值变化趋势');
3 仿真结果
4 参考文献
[1]黄祎, 孙德宝, and 秦元庆. "基于粒子群算法的移动机器人路径规划." 兵工自动化 25.4(2006):3.
