目录
前言
提示:这里可以添加本文要记录的大概内容:
例如:哈希表是一种非常重要的数据结构。
提示:以下是本篇文章正文内容,下面案例可供参考
一、哈希表是什么?
哈希表通常是基于数组实现的,但它又有很多自己的优点与不足。
数组的优缺点:
- 数组进行插入操作时,效率比较低
- 数组进行查找/删除时:
- 如果是基于索引查找效率非常高
- 如果基于内容查找则效率很低
哈希表:
????????
哈希函数:
????????![]()
?
二、哈希表详解
字符编码:?
- Ebcdic
- ASCII?
- ISO-8859-1
- GBxxxx? :GB2312、GBK、GB18030
- Unicode:UTF-32、UTF-16、UTF-8
哈希化:将大数字转化成数组范围内下标的过程,称之为哈希化。
哈希函数:通常我们会将单词转成大数字,大数字在进行哈希化的代码实现放在一个函数中,这个函数称为哈希函数。
哈希表:最终将数据插入到的这个数组,对整个结构的封装,称之为是一个哈希表。
冲突:哈希化后的下标值重复问题
解决冲突的办法:
- 链地址法
- 开放地址法
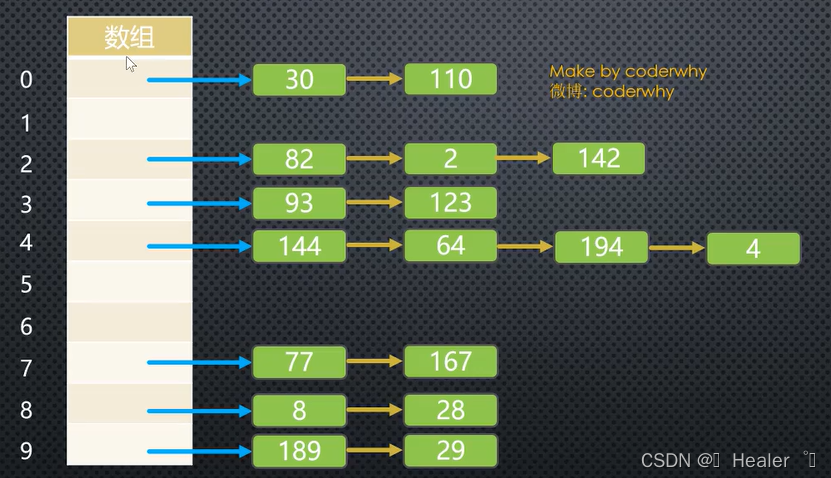
链地址法(拉链法):每个数组单元中存储的不再是单个数据,而是一个数组或者链表(两者均可,因为二者查找的效率差不多,根据业务x)
????????
开放地址法:寻找空白的单元格来添加重复的数据。
????????
开放地址法中探索位置(寻找空白位置)的方式不同,有三种方法:
- 线性探测
- 二次探测
- 再哈希法
线性探测:
- ????????插入:从index位置+1开始一点点查找合适的位置,空的位置就是合适的位置。
- ????????查询? :? ? ?从index位置+1开始查找和target一样的数据 ,在查询过程中有一个约定:查询到空位置则停止。
- ? ? ? ? 删除:删除操作一个数据项时,不可以将这个位置下标的内容设置为null,因为设置为null可能会影响后面的查询其他操作,通常删除一个位置的数据项时,可以将它进行特殊处理(比如设置为-1),当看到-1位置的数据项时,就知道查询时要继续查询,但是插入时这个位置可以放置数据。
? ? ? 线性探测的问题:
????????????????聚集:这种一连串填充单元。
? ? ? ? ? ? ? ? 聚集会影响哈希表的性能,无论是插入/查询/删除都会影响。
二次探测:二次探测优化的是探测时的步长,比如从下标值x开始,x+1的2次方,x+2的2次方,x+3的2次方……这样就可以一次性探测比较长的位置,避免聚集带来的问题。
? ? ? ? 但是会带来步长不一的聚集。
再哈希法:为了消除线性探测和二次探测中无论步长+1还是步长+平法中存在的问题。
? ? ? ? 二次探测的算法产生的探测步长是固定的1,4,9,16,以此类推。
? ? ? ? 现在需要一种方法:产生一种依赖关键字的探测序列,而不是每个关键字都一样。
? ? ? ? 那么,不同的关键字即使映射到相同的数组下标,也可以使用不同的探测序列。
? ? ? ? 再哈希法的做法就是:把关键字用另外一个哈希函数,再做一次哈希化,用这次哈希化的结果作为步长。
? ? ? ? 对于指定的关键字,步长在整个探测中是不变的,不过不同的关键字使用不同的步长。
第二次哈希化需要具备的特点:
- 和第一个哈希函数不同
- 不能输出为0
哈希化的效率:
????????
?通常认为二次探测和再哈希化性能差不多,比线性探测性能好一点。
链地址法相对来说效率是好于开放地址法的。
哈希函数:
? ? ? ? 提高速度的办法:在哈希函数中尽量少用乘法和除法。
好的哈希函数的优点:
- ????????快速的计算
- ????????均匀的分布
多项式的优化算法:霍纳法则-秦九韶算法
????????
时间复杂度:O
均匀分布:在使用常量的地方,尽量使用质数。
质数的使用:
- ? ? ? ? 哈希表的长度(哈希表的哈希表的长度尽量为质数:判断质数,如果是则使用,如果不是则num++,直到质数为止。)
- ? ? ? ? N次幂的底数
哈希表的扩容思想:
????????
?????????
?扩容+缩容
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了哈希表。