分数的四则运算
前言
??在数学问题中,我们会经常遇到分数。当然我们可以很轻松的使用两个数相除的形式来表达分数,但是如何进行分数的化简以及四则运算呢?
分数的表示
??还记得分数有一种无论分子比分母大或者小,都保留其原数的假分数形式吗?在代码中我们可以使用假分数的形式表示分数,因此可以用结构体来存储分数。
struct Fra{
int up, down;//up分子、down分母
};
但是要对这种表示制定三项规则:
- 如果分数为负数,则令分子up为负数即可。
- 如果该分数恰为0,则令分子为0,分母为1。
- 分子分母没有除了1以外的公约数。
那么我们如何保证我们的分数第三条和第一条规则呢,这就需要对分数进行化简。
分数的化简
??我们在刚接触分数并且对其化简时,首先要判断分子和分母有没有公约数,因此当我们求得分子和分母的最大公约数后,就可以很快地对分数进行化简。关于如何求两个数的最大公约数你可以在我的另一篇帖子:【C++】常见数学问题:数字黑洞 & 求最大公约数 & 求最小公倍数 找到详细的解释。在知道了如何求两个数的最大公约数以后,我们便可以写出如下代码:
//分数的化简
Fra reduction(Fra res){
if(res.down < 0){//如果分母为负数,则对分子分母同时取相反数
res.up = -res.up;
res.down = -res.down;
}
if(res.up == 0) res.down = 1;
else{
int d = gcd(abs(res.up), abs(res.down));//求分子分母的最大公约数
res.up /= d;//除去最大公约数,对分数进行化简
res.down /= d;
}
return res;
}
在我们知道了分数的化简之后,我们就可以根据分数四则运算规律很快的写出相应代码。
分数的四则运算
分数的加法
//分数的加法
Fra add(Fra f1, Fra f2){
Fra res;
res.up = f1.up * f2.down + f2.up * f1.down;//f1分子乘以f2分母加上f2分子乘以f1分母
res.down = f1.down * f2.down;//两分母相乘
return reduction(res);//化简
}
分数的减法
//分数的减法
Fra minu(Fra f1, Fra f2){
Fra res;
res.up = f1.up * f2.down - f2.up * f1.down;//f1分子乘以f2分母减去f2分子乘以f1分母
res.down = f1.down * f2.down;//两分母相乘
return reduction(res); //化简
}
分数的乘法
//分数的乘法
Fra multi(Fra f1, Fra f2){
Fra res;
res.up = f1.up * f2.up;//f1分子乘以f2分子
res.down = f1.down * f2.down; //两分母相乘
return reduction(res);//化简
}
分数的除法
//分数的除法
Fra divide(Fra f1, Fra f2){
Fra res;
res.up = f1.up * f2.down;//f1分子乘以f2分母
res.down = f2.up * f1.down;//f2分子乘以f1分母
return reduction(res);//化简
}
分数的输出
计算完成后,我们输出分数时,如果分母是1,可见此时结果是整数。当分子大于分母时,此时应该以带分数的形式输出。
//分数的输出
void result(Fra f){
f = reduction(f);
if(f.down == 1) cout<<f.up;
else if(abs(f.up) > f.down) cout<<f.up/f.down<<" "<<abs(f.up) % f.down<<"/"<<f.down;
else cout<<f.up<<"/"<<f.down;
}
样例测试
下面我们来写个样例测试一下。
int main(){
Fra f1, f2;
cin>>f1.up>>f1.down;
cin>>f2.up>>f2.down;
cout<<"两分数相加结果为:";
result(add(f1, f2));
cout<<endl;
cout<<"两分数相减结果为:";
result(minu(f1, f2));
cout<<endl;
cout<<"两分数相乘结果为:";
result(multi(f1, f2));
cout<<endl;
cout<<"两分数相除结果为:";
result(divide(f1, f2));
cout<<endl;
return 0;
}
运行结果如下:
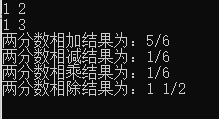
算法笔记专栏持续更新中,期待各位关注。本文如有错误,欢迎各位在评论区指正。