简介：

在经过采样之后，如何能够恢复原来的时域信号呢？这就涉及到信号的重构这个问题了。关于采样的细节读者可以回顾专栏的【信号处理】采样定理的深入浅出这篇文章。本篇文章将介绍重构信号原理，并加以仿真。

一、原理分析

根据采样定理一篇中我们可以知道，采样后，频域周期化，无失真采样准则就是频域周期化后不混叠，然后我们就能通过一个LPF（Low Pass Filter）将信号给复原。

其过程如下所示：

那么我们又知道，根据傅里叶变换定理，频域的相乘就是时域的卷积。理想低通滤波器的时域表达式是：

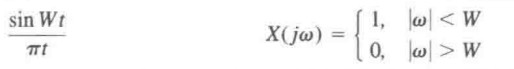
?它是一个sinc函数，波形如下：

?所以，就是拿着这个sinc函数去和采样后的值进行卷积。其数学表达式和图像是：

?可以清晰地看到，两个sinc波形之间的主要部分互相叠加，使得叠加后的值几乎复原原信号，而某一sinc函数的其他部分与其他sinc函数的其他部分正负抵消，对原本采样得到的值影响非常小，所以可以复原重构出原来的信号。这就是信号的重构。

二、MATLAB 仿真

这里一定注意内插函数的设计，若内插函数不合理的话，复原的波形会很奇怪。

%%
clear;clc;
% Generation of signals
nT=[0:0.5:3]; % Sampling interval is 0.5
xd=sin(nT)+cos(2*nT)+sin(4*nT); % signal after sampling
t=[0:0.01:3]; % Original signal interval
xt=sin(t)+cos(2*t)+sin(4*t);  % Original signal
%%
% Low pass filter - Interpolation in time domain
[~,nov]=size(xd); % Get the amount of value as nov
inter_points=5;  % Interpolation points are 5
it=[-inter_points*0.5/(inter_points+1):0.5/(inter_points+1):inter_points*0.5/(inter_points+1)];
ht=sinc((pi*0.5)*it); % interpolation function ht
x_lpf=zeros(nov*(inter_points+1),1); % signal after Low pass filter

for i=2:1:nov-1 % Interpolation
    buffer=ht'.*xd(i);
    x_lpf((i-1)*(inter_points+1)-inter_points:(i-1)*(inter_points+1)+inter_points,1)=buffer(:,1)+...
        x_lpf((i-1)*(inter_points+1)-inter_points:(i-1)*(inter_points+1)+inter_points,1);
end
ht_left=ht(inter_points+1:end)';
ht_right=ht(1:inter_points+1)';
x_lpf(1:inter_points+1)=x_lpf(1:inter_points+1)+ht_right;
x_lpf(end-inter_points:end)=x_lpf(end-inter_points:end)+ht_left;

%%
nT_=[0:0.5/(inter_points+1):3+0.5*inter_points/(inter_points+1)];
figure('name','Test');
subplot 131;plot(nT,xd);title('Signal after sampling')
subplot 132;plot(nT_,x_lpf);xlim([0 3]);title('Signal after Reconstruction');
subplot 133;plot(t,xt);title('Original Signal');

结果：