1 简介
本文提出一种麻雀算法优化基于最小二乘支持向量机的数据预测方法。LSSVM 是一种新型机器学习算法,其在传统支持向量机 SVM 基础上,将二次规划问题中的不等式约束改为等式约束,极大地方便了求解过程,克服了数据集粗糙、数据集波动性大等问题造成的异常回归,能有效避免 BP 神经网络等方法中出现的局部最优等问题。
麻雀搜索算法(?sparrow search algorithm,SSA)?是新群智能优化算法,具有良好的全局搜索能力和?快速收敛性。与其他群智能算法一样来源于对生物体觅食情况的观察,麻雀种群在觅食过程中分为?两个部分: 发现者和加入者。发现者负责搜索食物?并为种群中的其他个体提供觅食区域和方向,通常?是具有高能源储备的个体,其所对应的适应度函数?值更优。加入者对应为适应度函数值较差的个体,?它们通过发现者留下的信息获得食物。适应度值?最差的部分麻雀找不到食物,为了寻找到食物它们?可能跳出当前的搜索区域,到其他的地方觅食。种?群中的每只麻雀都会监视其他同伴的行为,并且部?分麻雀会攻击摄取量较高的同伴争夺资源。当种?群中个别麻雀发现捕食者后发出报警信号,一旦报?警值大于安全值时发现者会把加入者带到其他安?全的区域觅食。?种群中发现者和加入者的总数和比例不变,但?是两者的身份是动态变化的。寻找到更好的食物?来源的任何一只麻雀都可能变成发现者,此时其所?对应的适应度值变优,与此同时必然会有一只麻雀变成加入者,其适应度值变差。加入者的能量值越?低,在搜索范围内的位置对自己越不利越不容易找?到食物,这些极其渴望得到食物的麻雀可能飞到别的领域觅食,从而使自己获得能量。在整个觅食的过程中,加入者能搜索到能量更高的发现者,从而?获得食物或者伺机夺取食物。?当意识到可能有危险时,为了获得更安全的位?置,种群边缘的麻雀快速向安全范围内移动,而在?种群中间的麻雀随机走动靠近其他的同伴。?
算法流程如下:
步骤1,采集时间序列的样本数据;
步骤2,建立基于麻雀搜索算法优化参数的LSSVM数据预测模型;
步骤3,应用预测模型对训练样本进行预测,得到训练样本的相对误差和预测值;步骤4,预测模型对训练样本的相对误差进行预测,从而得到相对误差的预测值;步骤5,对相对误差的预测值进行校正,从而得到预测速率;解决了由于最小二乘支持向量机核函数参数和惩罚参数的经验性赋值而导致的预测精度不足的问题.
2 部分代码
? ?%=====================================================================
%初始化
clc
close?all
clear
format?long
tic
%==============================================================
%%导入数据
data=xlsread('1.xlsx');
[row,col]=size(data);
x=data(:,1:col-1);
y=data(:,col);
set=1;?%设置测量样本数
row1=row-set;%
train_x=x(1:row1,:);
train_y=y(1:row1,:);
test_x=x(row1+1:row,:);%预测输入
test_y=y(row1+1:row,:);%预测输出
train_x=train_x';
train_y=train_y';
test_x=test_x';
test_y=test_y';
%%数据归一化
[train_x,minx,maxx,?train_yy,miny,maxy] =premnmx(train_x,train_y);
test_x=tramnmx(test_x,minx,maxx);
train_x=train_x';
train_yy=train_yy';
train_y=train_y';
test_x=test_x';
test_y=test_y';
%% 参数初始化
%粒子群算法中的两个参数
c1?=?1.5;%; % c1 belongs to [0,2] c1:初始为1.5,pso参数局部搜索能力,表征个体极值对当前解得影响
c2?=?1.7;%; % c2 belongs to [0,2] c2:初始为1.7,pso参数全局搜索能力,表征全局极值对当前解得影响
maxgen=100;?% 进化次数 300
sizepop=30;?% 种群规模30
popcmax=10^(3);% popcmax:初始为1000,SVM 参数c的变化的最大值.
popcmin=10^(-1);% popcmin:初始为0.1,SVM 参数c的变化的最小值.
popgmax=10^(2);% popgmax:初始为100,SVM 参数g的变化的最大值
popgmin=10^(-2);% popgmin:初始为0.01,SVM 参数g的变化的最小值.
k?=?0.5;?% k belongs to [0.1,1.0];
itness(j) =?fitness(j);
? ? ? ?end
? ? ? ?
? ? ? ?%群体最优更新
? ? ? ?if?fitness(j)?<?global_fitness
? ? ? ? ? ?global_x?=?pop(j,:);
? ? ? ? ? ?global_fitness?=?fitness(j);
? ? ? ?end
? ? ? ?
? ? ? ?if?abs(?fitness(j)-global_fitness?)<=eps?&&?pop(j,1)?<?global_x(1)
? ? ? ? ? ?global_x?=?pop(j,:);
? ? ? ? ? ?global_fitness?=?fitness(j);
? ? ? ?end
? ?end
? ?fit_gen(i)=global_fitness;
? ?avgfitness_gen(i) =?sum(fitness)/sizepop;
? ?
? ?%if global_fitness<0.00005%设定终止条件,避免网络过度训练,影响推广能力。
? ?%break;
? ?%end
? ?
end
%% 结果分析
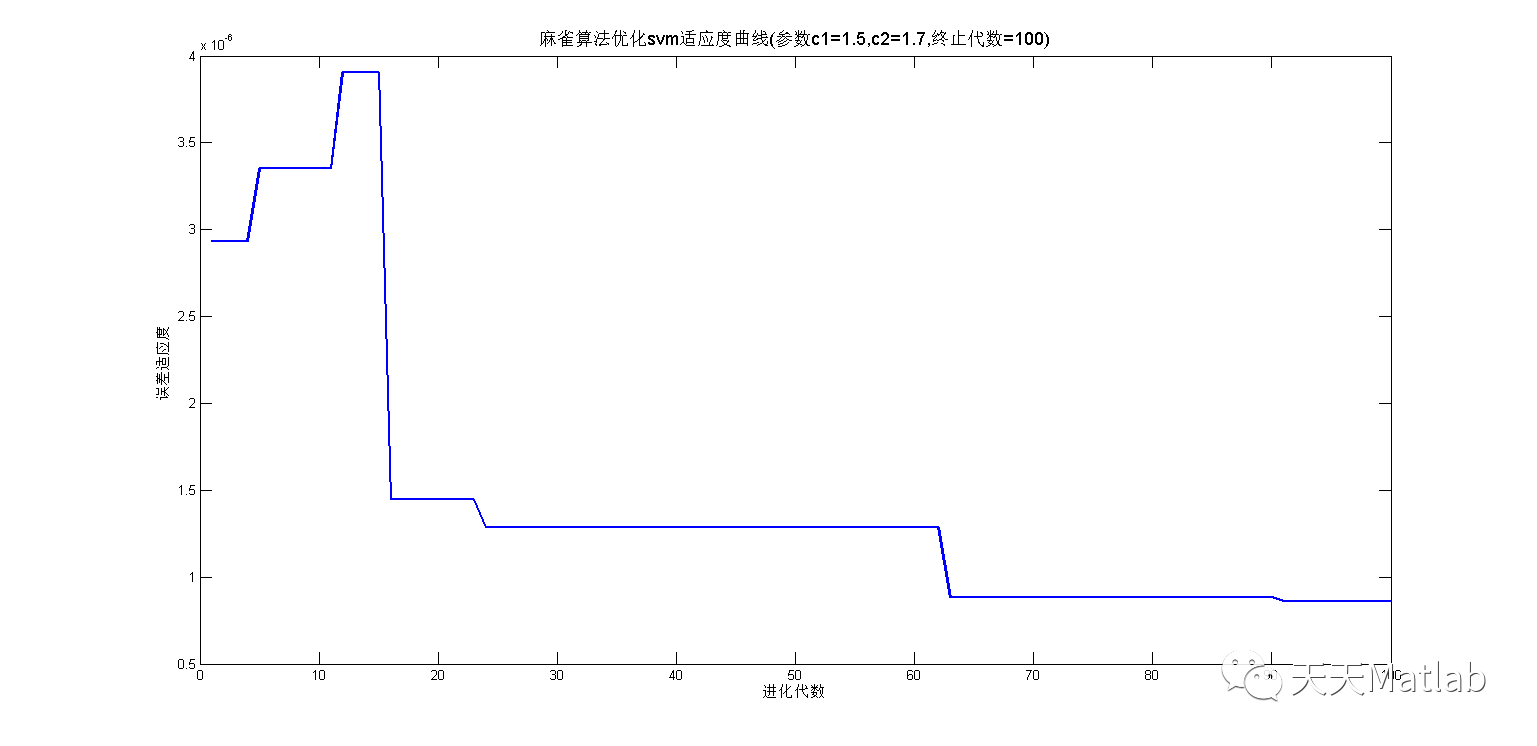
plot(fit_gen,'LineWidth',2);
title(['麻雀算法优化svm适应度曲线','(参数c1=',num2str(c1),',c2=',num2str(c2),',终止代数=',num2str(maxgen),')'],'FontSize',13);
xlabel('进化代数');ylabel('误差适应度');
bestc?=?global_x(1);
bestg?=?global_x(2);
gam=bestc
sig2=bestg
model=initlssvm(train_x,train_yy,type,gam,sig2,kernel,proprecess);%原来是显示
model=trainlssvm(model);%原来是显示
%求出训练集和测试集的预测值
[train_predict_y,zt,model]=simlssvm(model,train_x);
[test_predict_y,zt,model]=simlssvm(model,test_x);
%预测数据反归一化
train_predict=postmnmx(train_predict_y,miny,maxy);%预测输出
test_predict=postmnmx(test_predict_y,miny,maxy);
%计算均方差
trainmse=sum((train_predict-train_y).^2)/length(train_y)
%testmse=sum((test_predict-test_y).^2)/length(test_y)
for?i=1:set
? ?RD(i)=(test_predict(i)-test_y(i))/test_y(i)*100;
end
for?i=1:set
? ?D(i)=test_predict(i)-test_y(i);
end
RD=RD'
D=D'
figure
plot(test_predict,':og')
hold?on
plot(test_y,'- *')
legend('预测输出','期望输出')
title('网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
figure
plot(train_predict,':og')
hold?on
plot(train_y,'- *')
legend('预测输出','期望输出')
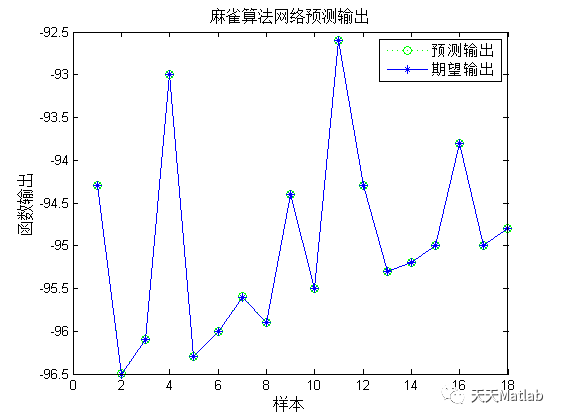
title('麻雀算法网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
toc???%计算时间
3 仿真结果
4 参考文献
[1]聂敬云, 李春青, 李威威, & 王韬. (2015). 关于遗传算法优化的最小二乘支持向量机在mbr仿真预测中的研究. 软件(5), 6.
[2]胡林静, 郭朝泽, 王景帅. 基于ISSA-LSSVM模型的短期电力负荷预测[J]. 科学技术与工程, 2021, 21(23):7.
