[数据结构与算法]二叉树code

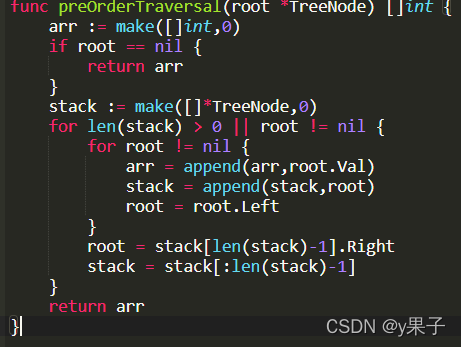
1. 前序遍历二叉树

func preOrder(node *TreeNode){
    if node == nil {
        return 
    }
    pre = append(pre,node.Val)
    preOrder(node.Left)
    preOrder(node.Right)
}

func preOrderTraversal(root *TreeNode) []int {
    arr := make([]int,0)
    if root == nil {
        return arr
    }
    stack := make([]*TreeNode,0)
    for len(stack) > 0 || root != nil {
        for root != nil {
            arr = append(arr,root.Val)
            stack = append(stack,root)
            root = root.Left
        }
        root = stack[len(stack)-1].Right
        stack = stack[:len(stack)-1]
    }
    return arr
}

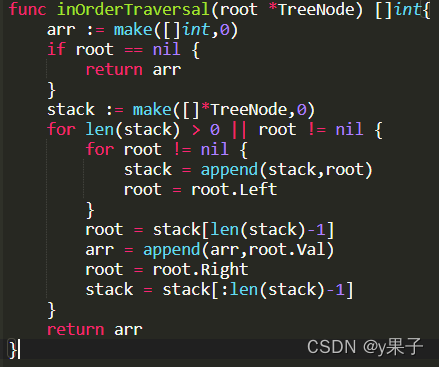
2. 中序遍历二叉树

func inOrder(node *TreeNode){
    if node == nil {
        return 
    }   
    inOrder(node.Left)
    in = append(in,node.Val)
    inOrder(node.Right)
}

func inOrderTraversal(root *TreeNode) []int{
    arr := make([]int,0)
    if root == nil {
        return arr
    }
    stack := make([]*TreeNode,0)
    for len(stack) > 0 || root != nil {
        for root != nil {
            stack = append(stack,root)
            root = root.Left
        }
        root = stack[len(stack)-1]
        arr = append(arr,root.Val)
        root = root.Right
        stack = stack[:len(stack)-1]
    }
    return arr
}

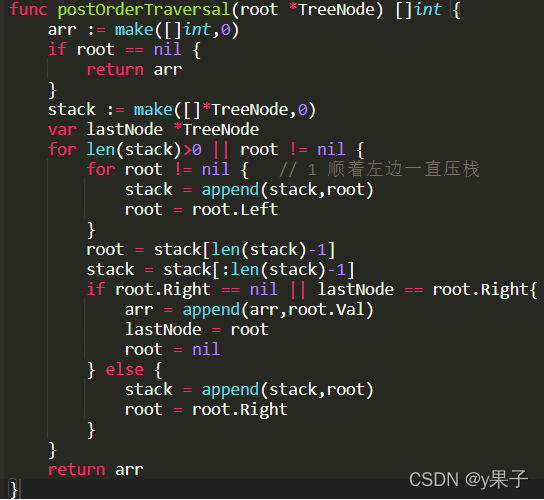
3. 后序遍历二叉树

func postOrder(node *TreeNode) {
    if node == nil {
        return
    }
    postOrder(node.Left)
    postOrder(node.Right)
    post = append(post,node.Val)
}

func postOrderTraversal(root *TreeNode) []int {
    arr := make([]int,0)
    if root == nil {
        return arr
    }
    stack := make([]*TreeNode,0)
    var lastNode *TreeNode
    for len(stack)>0 || root != nil {
        for root != nil {   // 1 顺着左边一直压栈
            stack = append(stack,root)
            root = root.Left
        }
        root = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        if root.Right == nil || lastNode == root.Right{
            arr = append(arr,root.Val)
            lastNode = root
            root = nil
        } else {
            stack = append(stack,root)
            root = root.Right
        }
    }
    return arr
}

1. 二叉树的深度

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度，根节点的深度视为 1 。
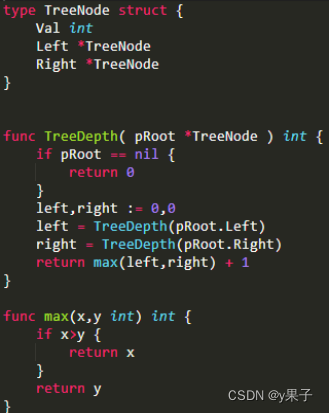
递归法：
最终结果为 max( 头结点左子树的最大深度, 头结点右子树的最大深度)+1。
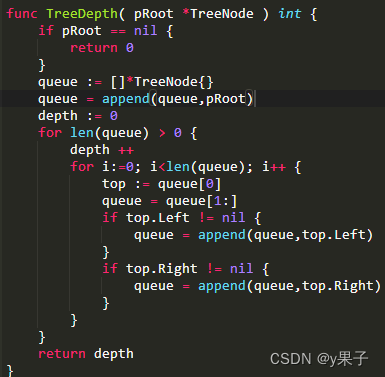
层序遍历：
二叉树的层次遍历，一般我们都是用队列去实现的。
1、先创建一个队列，将根节点入队；
2、队列不为空，进入循环：
出队一个节点
将当前节点的左右节点入队（不为空时）
3.此时当前层的所有节点的左右子节点都入队
4、最后当队列中无节点的时候，此时已全部遍历完全部节点。
只需要在每一层的所有节点的左右子节点都入完队的时候，就计数。

2. 按之字形顺序打印二叉树

给定一个二叉树，返回该二叉树的之字形层序遍历，（第一层从左向右，下一层从右向左，一直这样交替）
输入：{1,2,3,#,#,4,5}
返回值：[[1],[3,2],[4,5]]
说明：如题面解释，第一层是根节点，从左到右打印结果，第二层从右到左，第三层从左到右。
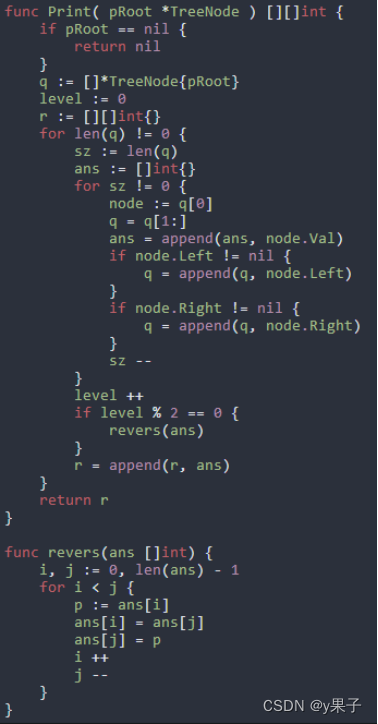
算法流程：
1、特殊情况：如果树的根节点为空，则直接返回 【】
2、初始化：返回列表 res ，二叉树层索引 index，辅助栈
3、层次遍历循环 当栈为空跳出：
1、新建列表tmp，用于临时存储当前层打印结果
2、当前层打印循环：循环次数为当前层节点数量
1、出栈：栈底元素，记为 node
2、打印：将所在层节点值添加到 tmp中
3、添加子节点：若 node 的左右子树不为空，则 入栈
3、根据index判断所在层是奇数层还是偶数层：
1、若为奇数层：将tmp直接添加到res中
2、若为偶数层：将tmp倒序添加到res中
4、index 加1
4、返回打印结果 res

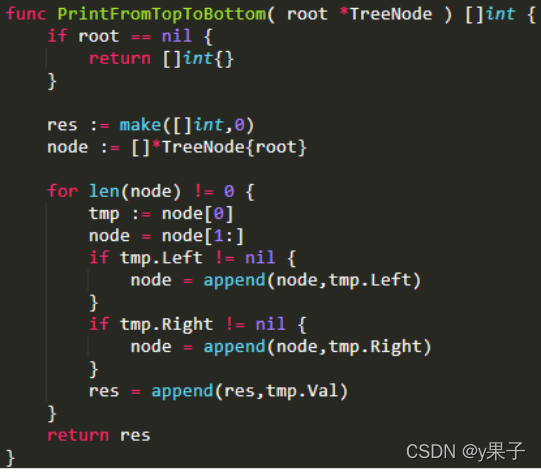
3. 从上到下打印二叉树

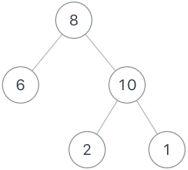
不分行从上往下打印出二叉树的每个节点，同层节点从左至右打印。例如输入{8,6,10,#,#,2,1}，如以下图中的示例二叉树，则依次打印8,6,10,2,1(空节点不打印，跳过)，请你将打印的结果存放到一个数组里面，返回。

4 .把二叉树打印成多行

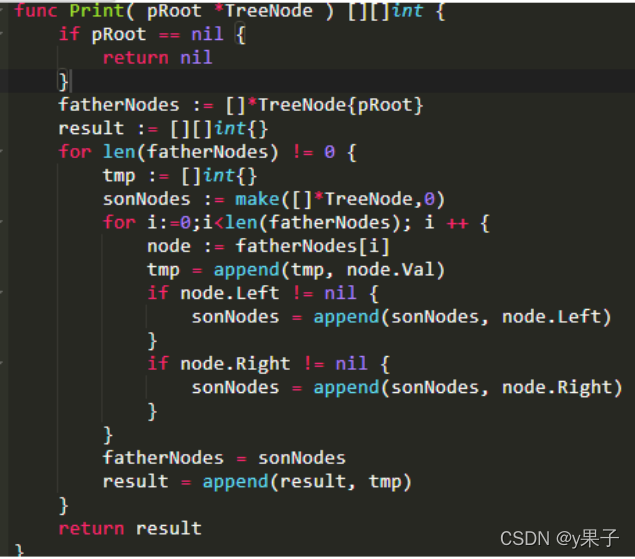
给定一个节点数为 n 二叉树，要求从上到下按层打印二叉树的 val 值，同一层结点从左至右输出，每一层输出一行，将输出的结果存放到一个二维数组中返回。
给定的二叉树是{1,2,3,#,#,4,5}

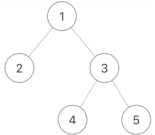
该二叉树多行打印层序遍历的结果是
[[1],[2,3],[4,5]]

5. 重建二叉树

给定节点数为 n 二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

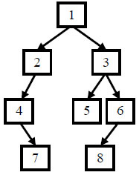
输入：[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]
返回值：{1,2,3,4,#,5,6,#,7,#,#,8}
说明：返回根节点，系统会输出整颗二叉树对比结果，重建结果如题面图示。

二叉树的前序遍历：根左右；中序遍历：左根右
由前序遍历知道根节点之后，能在中序遍历上划分出左子树和右子树。分别对中序遍历的左右子树递归进行这一过程即可建树。

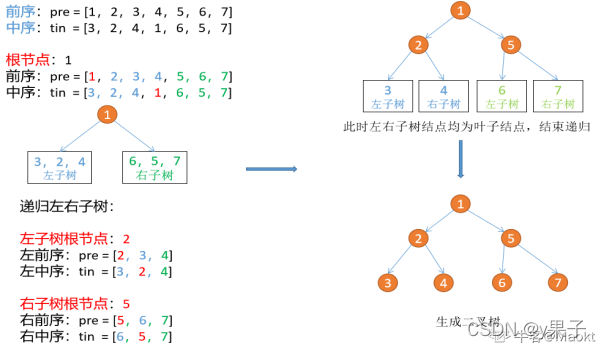
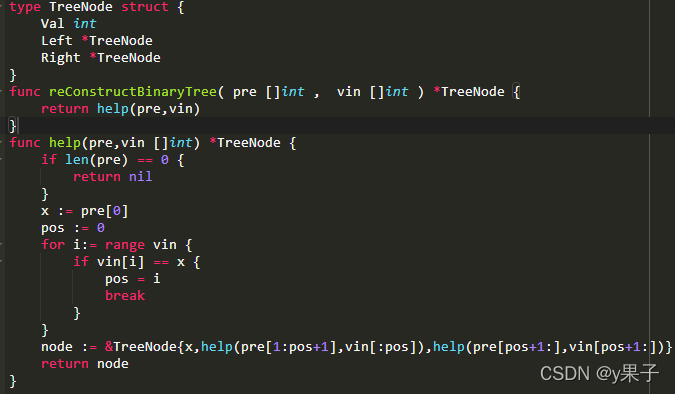
6. 树的子结构(B是不是A的子结构)

输入两棵二叉树A，B，判断B是不是A的子结构。（我们约定空树不是任意一个树的子结构）假如给定A为{8,8,7,9,2,#,#,#,#,4,7}，B为{8,9,2}，2个树的结构如下，可以看出B是A的子结构。

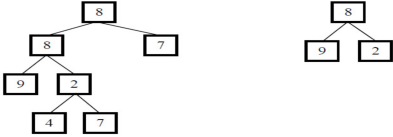
递归：
1.判断是否是子结构，主要看pRoot2和pRoot1的根节点的值是否一样，一样的话再同时递归，
2.判断left节点，如果pRoot2的左节点为null,则说明pRoot2的left节点满足条件。
3.若pRoot2的节点不为null,并且pRoot1的left节点为null,或者说它们二者的值不一样，说明pRoot2不是pRoot1的子结构。
4.pRoot1和pRoot2的right节点和第2.3步一样的判断，当left和right同时成立，pRoot2才是pRoot1的子结构
5.因为题目约定空树不是任意一个数的子结构，所以pRoot1和pRoot2都不能为空，这是返回true的前提条件

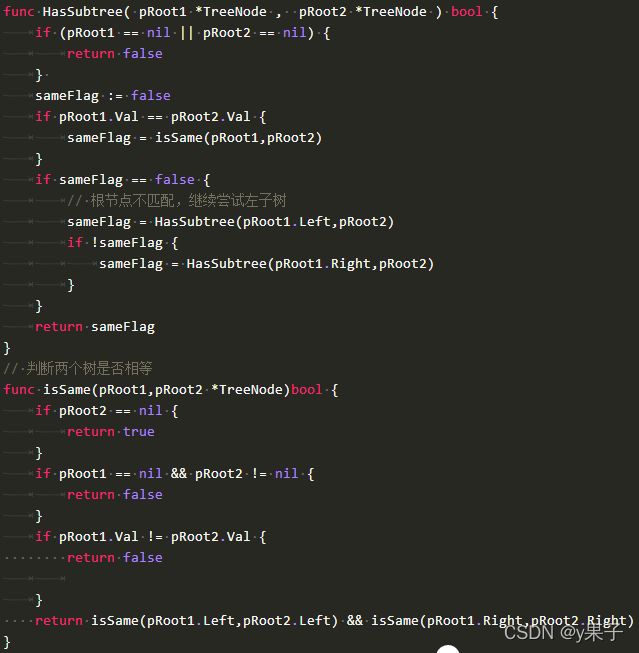
非递归：
1.先遍历树pRoot1，如果遍历到和pRoot2节点值相同的节点，进入isSubTree方法判断接下来的节点是否都相同。
2.节点都相同返回True；不相同返回False，并且继续遍历树pRoot1找下一个相同的节点。
3.如果遍历完了pRoot1还没有返回过True，说明pRoot2不是pRoot1的子结构，返回False。
isSubTree方法：用于判断从pRoot1的子树是否有和pRoot2相同的部分
1.采用递归的思想，如果节点root1与root2的节点不同，则说明pRoot1的子树与pRoot2不具有相同的节点
2.如果值相同，则递归判断（isSubTree）他们各自得左右节点的值是不是相同
3.递归的终止条件时到达pRoot1或pRoot2的叶节点

7. 二叉树的镜像

操作给定的二叉树，将其变换为源二叉树的镜像。
比如：
源二叉树 镜像二叉树

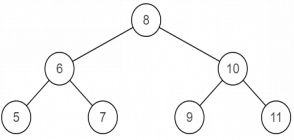
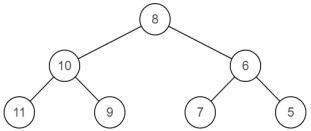
递归：交换每个节点的左 / 右子节点，即可生成二叉树的镜像。
解题步骤：
1、特判：如果pRoot为空，返回空
2、交换左右子树
3、把pRoot的左子树放到Mirror中镜像一下
4、把pRoot的右子树放到Mirror中镜像一下
5、返回根节点root

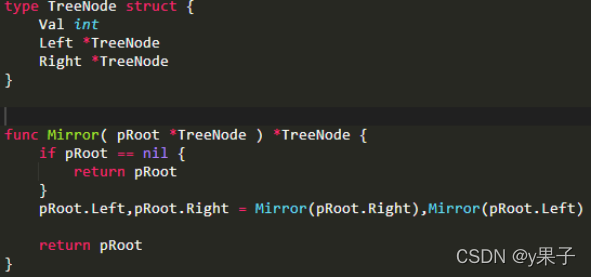
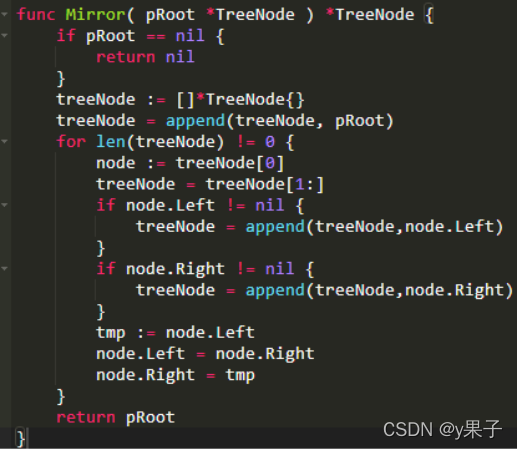
辅助栈/队列
利用栈（队列）遍历树的所有节点 node ，并交换每个 node 的左 / 右子节点
1、特例处理： 当 pRoot为空时，直接返回 null ；
2、初始化： 栈（或队列），本文用栈stack ，并加入根节点 pRoot。
3、循环交换： 当栈 stack 为空时跳出；
3.1、出栈： 记为 node ；
3.2、添加子节点： 将 node 左和右子节点入栈；
3.3、交换： 交换 node 的左 / 右子节点。
4、返回值： 返回根节点 pRoot 。

8. 二叉树中和为某一值的路径（一）

给定一个二叉树root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点，不能从子节点到父节点
4.总节点数目为n

给出如下的二叉树， sum=22

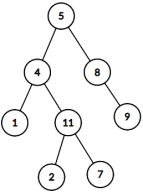
返回true，因为存在一条路径 5→4→11→2的节点值之和为 22

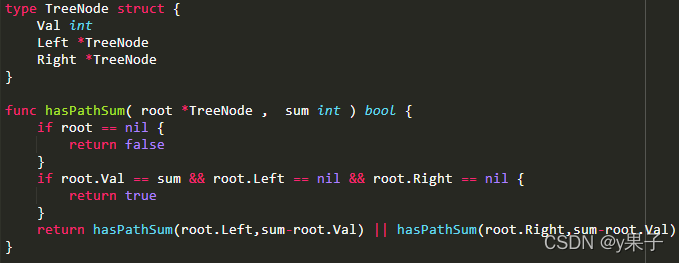
递归：
1、特殊情况：当二叉树为空，则返回 false
2、遍历根节点的左右子树，记录根节点的数字之和 res
当节点的左右子树均为空，且 res == sum，则返回 true
3、递归 该节点的左右子树，做上述计算

9. 二叉树中和为某一值的路径（二）

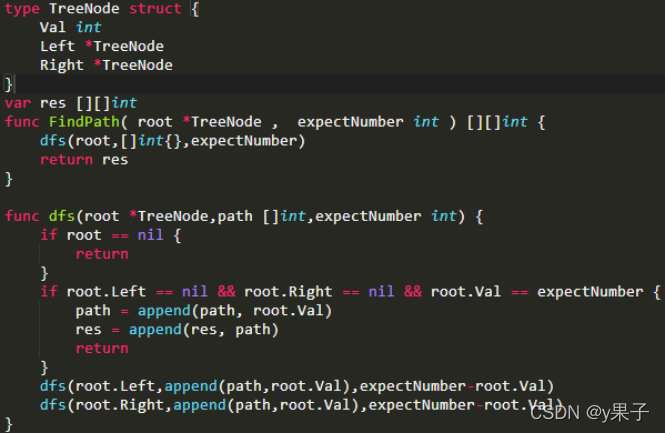
输入一颗二叉树的根节点root和一个整数expectNumber，找出二叉树中结点值的和为expectNumber的所有路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点，不能从子节点到父节点
4.总节点数目为n
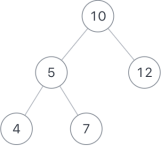
如二叉树root为{10,5,12,4,7},expectNumber为22
则合法路径有[[10,5,7],[10,12]]

10. 二叉树中和为某一值的路径（三）

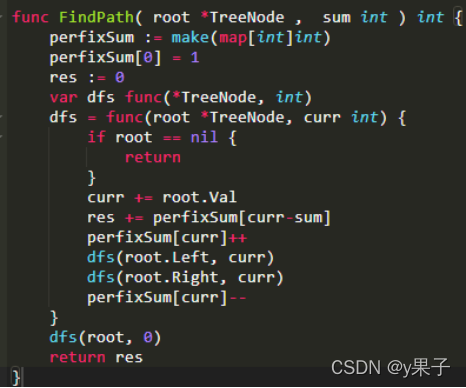
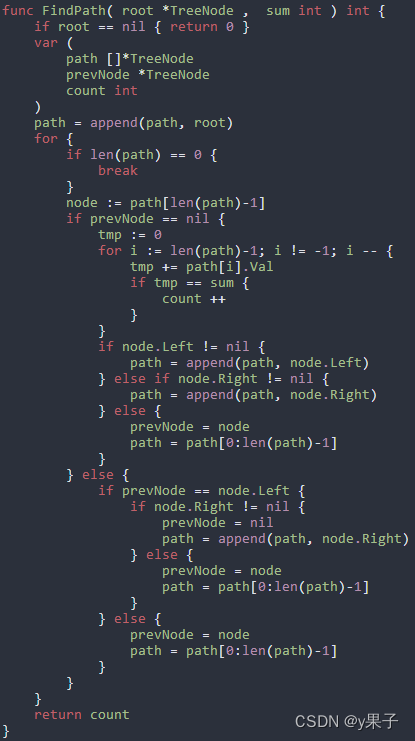
给定一个二叉树root和一个整数值 sum ，求该树有多少路径的的节点值之和等于 sum 。
1.该题路径定义不需要从根节点开始，也不需要在叶子节点结束，但是一定是从父亲节点往下到孩子节点
2.总节点数目为n
3.保证最后返回的路径个数在整形范围内(即路径个数小于231-1)

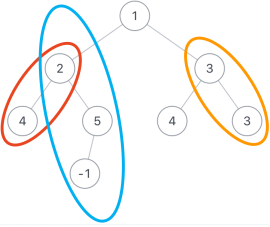
假如二叉树root为{1,2,3,4,5,4,3,#,#,-1}，sum=6，那么总共如下所示，有3条路径符合要求。

11. 二叉树的下一个结点

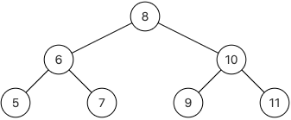
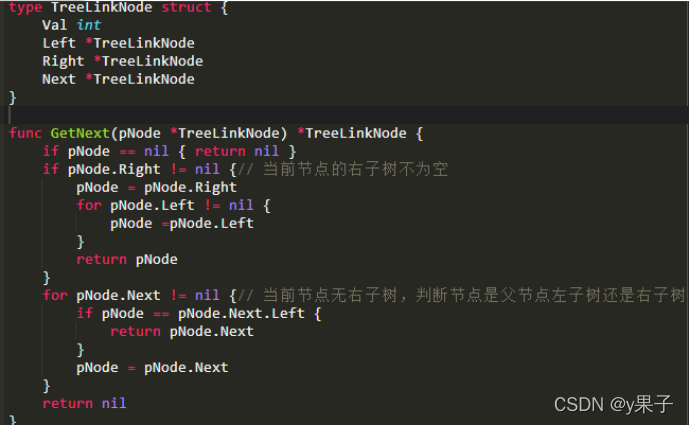
给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示。
输入:{8,6,10,5,7,9,11},8
返回:9
解析:这个组装传入的子树根节点，其实就是整颗树，中序遍历{5,6,7,8,9,10,11}，根节点8的下一个节点就是9，应该返回{9,10,11}，后台只打印子树的下一个节点，所以只会打印9。


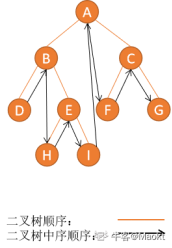
可以把中序（DBHEIAFCG）下一结点归为几种类型：
1、有右子树，下一结点是右子树中的最左结点，例如 B，下一结点是 H
2、无右子树，且结点是该结点父结点的左子树，则下一结点是该结点的父结点，例如 H，下一结点是 E
3、无右子树，且结点是该结点父结点的右子树，则一直沿着父结点追朔，直到找到某个结点是其父结点的左子树，如果存在这样的结点，那么这个结点的父结点就是我们要找的下一结点。例如 I，下一结点是 A；例如 G，并没有符合情况的结点，所以 G 没有下一结点。

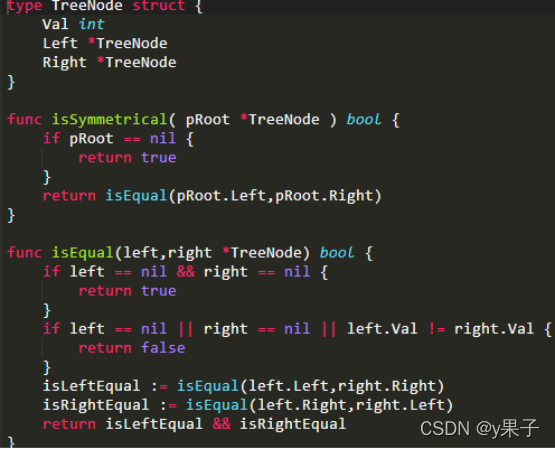
12. 对称的二叉树

给定一棵二叉树，判断其是否是自身的镜像（即：是否对称）
例如：下面这棵二叉树是对称的

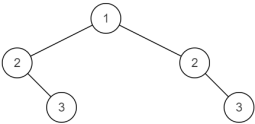
下面这棵二叉树不对称。

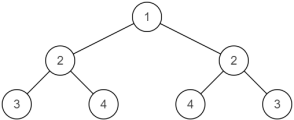
输入：{1,2,2,3,4,4,3}
返回值：true

递归：

若满足对称二叉树，必须满足：

L->val == R->val
L->left->val == R->right->val
L->right->val == R->left->val

• 设置一个递归函数isSame(r1, r2),表示如果对称，返回true，否则返回false
• 递归终止条件：r1nullptr && r2nulllptr, 直接返回true，否则，如果只有一个为nullptr，返回false
• 下一步递归：如果r1->val == r2->val, 则isSame(root1->left, root2->right) && isSame(root1->right, root2->left);

13. 序列化二叉树

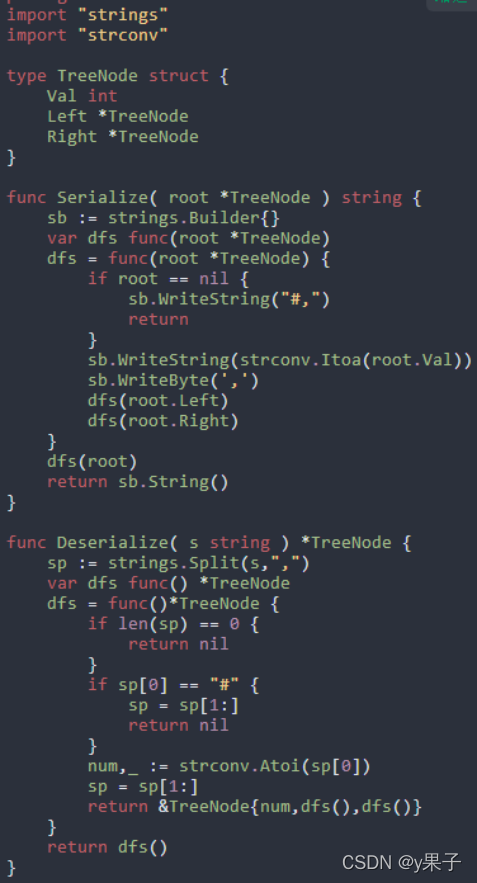
请实现两个函数，分别用来序列化和反序列化二叉树，不对序列化之后的字符串进行约束，但要求能够根据序列化之后的字符串重新构造出一棵与原二叉树相同的树。

二叉树的序列化(Serialize)是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树等遍历方式来进行修改，序列化的结果是一个字符串，序列化时通过某种符号表示空节点（#）

二叉树的反序列化(Deserialize)是指：根据某种遍历顺序得到的序列化字符串结果str，重构二叉树。

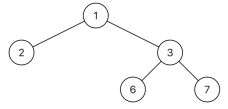
层序序列化(即用函数Serialize转化)如上的二叉树转为"{1,2,3,#,#,6,7}"，再能够调用反序列化(Deserialize)将"{1,2,3,#,#,6,7}"构造成如上的二叉树。

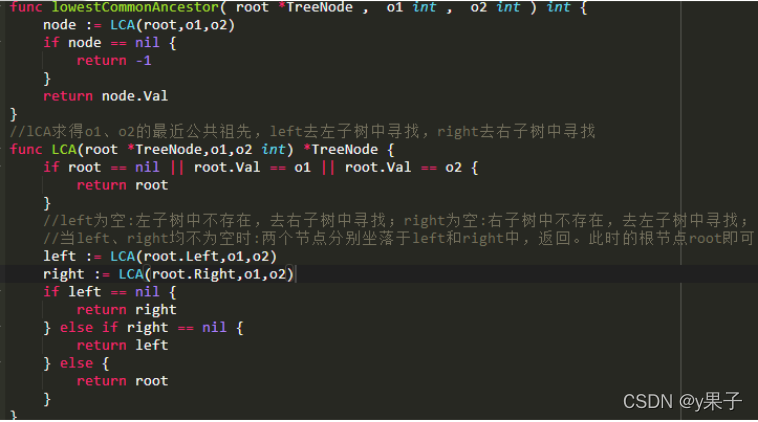
14. 在二叉树中找到两个节点的最近公共祖先

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。
如当输入[3,5,1,6,2,0,8,#,#,7,4],5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

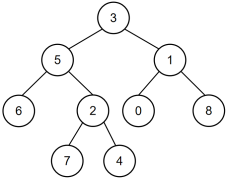
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

15 .二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

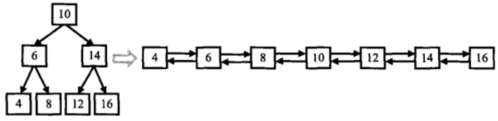
输入二叉树的节点数0≤n≤1000，二叉树中每个节点的值0≤val≤1000
要求：空间复杂度O(1)（即在原树上操作），时间复杂度 O(n)

注意:
1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构

将二叉搜索树进行中序遍历可以得到由小到大的顺序排列，因此本题最直接的想法就是进行中序遍历。
将中序遍历的结果用数组存储下来，得到的数组是有从小到大顺序的。最后将数组中的结点依次连接即可。

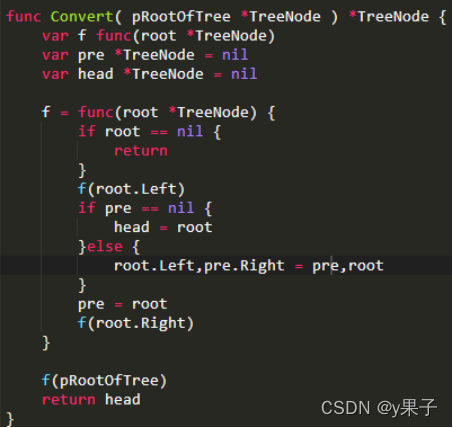
16 .二叉搜索树的后序遍历序列

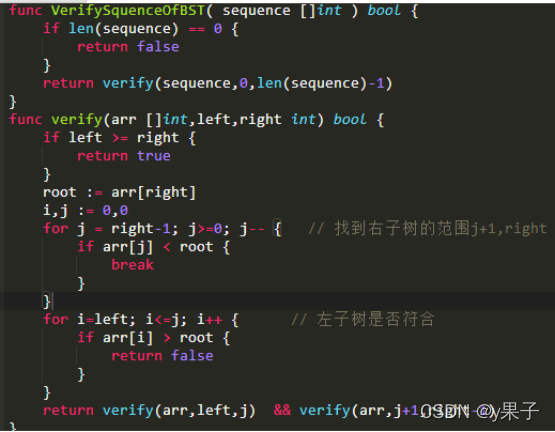
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true ,否则返回 false 。假设输入的数组的任意两个数字都互不相同。
数据范围： 节点数量0≤n≤1000 ，节点上的值满足1≤val≤10^5保证节点上的值各不相同。
要求：空间复杂度O(n) ，时间时间复杂度 O(n^2)
提示：
1.二叉搜索树是指父亲节点大于左孩子节点，但是小于右孩子节点。
2.该题我们约定空树不是二叉搜索树
3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历
4.参考下面的二叉搜索树，示例 1
分治法：

• 二叉树的后序遍历顺序是：左子树 -> 右子树 -> 根节点
• 因此序列的最后一个数代表了根节点
• 因此可以将一个序列划分为3段, 左子树+右子树+根, 如[4, 8, 6, 12, 16, 14, 10]可以根据根节点的值将其划分为左子树[4, 8, 6], 右子树[12, 16, 14], 根[10], 由于是先确定的右子树区间, 因此当左子树区间中出现大于根节点的值时, 序列不合法, 再采用分治的思想, 对于每段序列代表的子树, 检查它的左子树和右子树, 当且仅当左右子树都合法时返回true

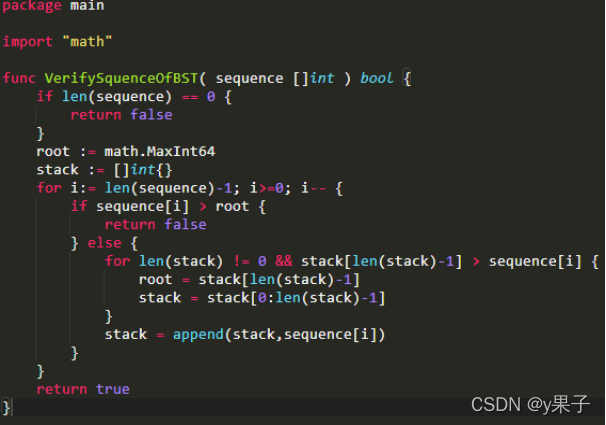
栈：

• 实际上二叉树的中序遍历和后序遍历对应着一种栈的压入、弹出序列, 而对后序遍历序列从小到大排序就得到了中序遍历序列
• 得到中序遍历序列后, 将其作为入栈序列, 检查后序遍历序列是不是一个合法的出栈序列即可

逆序后序遍历 + 辅助栈
后序遍历是“左节点 —> 右节点 —> 根节点”，那么逆序后序遍历就是：“根节点 ----> 右节点 ----> 左节点”。

按照这个思路，上面的示例( [4,8,6,12,16,14,10]）可以这么拆解（辅助栈只存储递增的节点）：

• 先把根节点10 添加到辅助栈 ([10])，然后遍历右子树。
• 如果右子树存在，那么下一个数一定是大于根节点的，且它是右子树的根节点（这里就是14），也把它添加到辅助栈中(此时为[10, 14]) ；依次类推，直到下一个数小于(这里就是12）右子树根节点，说明右子树已经遍历结束 (此时辅助栈中有[10,14,16]) 。
• 此时的这个小于根节点的数（就是 12），并不一定是左子树的子节点。所以这里需要判断：
• 先把刚刚压入的右子树节点都弹出栈(即弹出[14, 16])，此时栈只有一个元素(即[10])；
• 由于栈顶元素（10）小于 12，那么最后出栈的 14 就是这个 12 的父节点，把它也压入栈中，此时栈[10,12]。
• 下一个数是 6，又是小于当前栈中的栈顶元素 12，说明12没右子树；再次把[10,12]弹出栈，此时栈空。同理最后出栈的 10 就是 6的父节点！又把6 压入栈中，此时栈[6]。
• 同理后面的 8 ，是比栈顶元素 6 大的，所以入栈[6, 8]，且 6是 8的根节点。
• 最后的 4 比 [6, 8]小，所以[6, 8]依次出栈；且 4 是 6的左子节点。此时遍历结束，得到二叉搜索树如下：
  
  

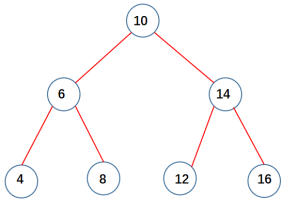
17. 二叉搜索树的第k个节点

二叉搜索树：中序遍历可以让结点有序的树。
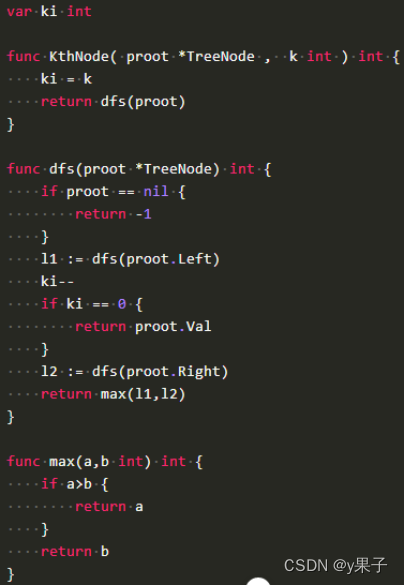
给定一棵结点数为n 二叉搜索树，请找出其中的第 k 小的TreeNode结点值。
1.返回第k小的节点值即可
2.不能查找的情况，如二叉树为空，则返回-1，或者k大于n等等，也返回-1
3.保证n个节点的值不一样

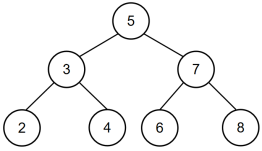
该二叉树所有节点按结点值升序排列后可得[2,3,4,5,6,7,8]，所以第3个结点的结点值为4，故返回对应结点值为4的结点即可。

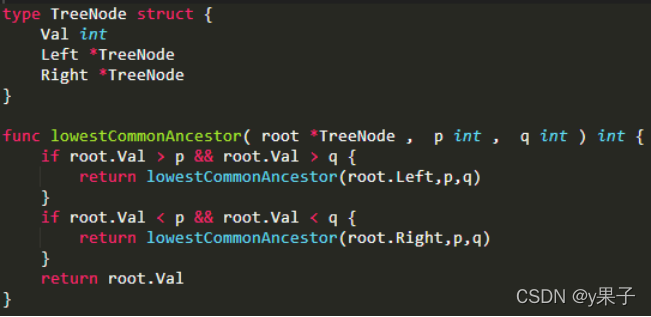
18.二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
1.对于该题的最近的公共祖先定义:对于有根树T的两个结点p、q，最近公共祖先LCA(T,p,q)表示一个结点x，满足x是p和q的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先.
2.二叉搜索树是若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
3.所有节点的值都是唯一的。
4.p、q 为不同节点且均存在于给定的二叉搜索树中。
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5}，如下图:

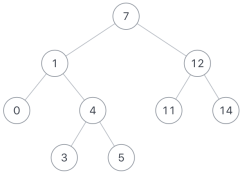
输入：{7,1,12,0,4,11,14,#,#,3,5},12,11
返回值：12
说明：因为一个节点也可以是它自己的祖先.所以输出12

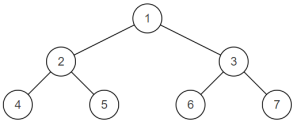
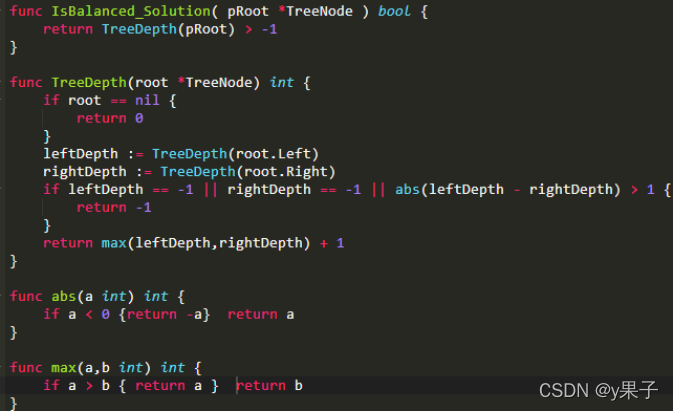
19. 判断是不是平衡二叉树

输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。
在这里，只需要考虑其平衡性，不需要考虑其是不是排序二叉树
平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

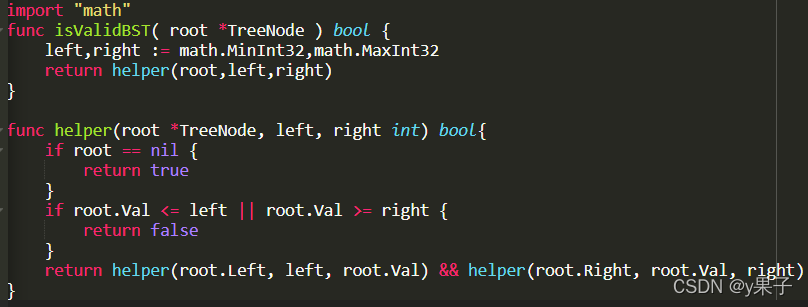
20. 判断是否为二叉搜索树

二叉搜索树的定义如下
一个节点的左子树上节点的值都小于自身的节点值
一个节点的右子树上节点的值都大于自身的节点值
所有节点的左右子树都必须是二叉搜索树

import "math"
func isValidBST( root *TreeNode ) bool {
    left,right := math.MinInt32,math.MaxInt32
    return helper(root,left,right)
}
func helper(root *TreeNode, left, right int) bool{
    if root == nil {
        return true
    }
    if root.Val <= left || root.Val >= right {
        return false
    }
    return helper(root.Left, left, root.Val) && helper(root.Right, root.Val, right)
}