排序算法-冒泡排序

代码

int a[8] = { 80, 2, 3, 24, 34, 90, 32, 43};
		for (int Z = 0; Z < 8; Z++)  //比较n-1轮
		{
			std::cout << a[Z] << " ";
		}
		std::cout << std::endl;
	
		for (int i = 0; i < 8 - 1; i++)  //比较n-1轮
		{
			for (int A = 0; A < 8 - 1 - i; A++)  //每轮比较8-1-i次,
			{
			int B = A+1;
				if (a[A] < a[B])
				{
					int tmp = a[A];
					a[A] = a[B];
					a[B] = tmp;
				}
			}
			for (int Z = 0; Z < 8; Z++)  //比较n-1轮
			{
				std::cout << a[Z] << " ";
			}
			std::cout << std::endl;
		}

结果

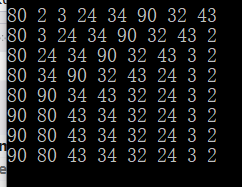
在这里插入图片描述

注释

数组大小为N，比较开始值的角标为A，被比较的值的角标为B

算法解释

比较思路

首选看第二个循环，在冒泡算法中A与B的关系为B = A+1;
再次看第二个循环，冒泡算法的比较思路为在将A的值与B的值进行比较，如果B与A的值满足条件，则发生值互换，而不论该次是否发生互换，则本次循环结束，A与B同时加1，直至B等于该数组最大值;

循环限制思路

此时返回第一个循环处：当第一个循环第一次结束后，满足条件的值已经被放至该数组最后一位；所以在第一个循环进入下一次后，则最后一位不需要再次进行比较；因此每一轮的循环后，都会在后面产生对应数量的不需要比较的值的数量，因此第二个循环不需要进行全部的比较排序；并且为了保证B值不会越界，所以在第二个循环中A值最大只能为该数组大小-1

并且，由比较思路可以看出，因为A与B的关系，因此该比较算法需要进行的大循环的次数为N-1次；

在这一过程中的数组中的每一个元素进行呼唤逐渐变为有序的过程就是冒泡排序