哈夫曼又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种
该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
作用:即利用哈夫曼算法的理论构建出字符char和对字符进行编码code,的一个二叉树的字典 如:a->101
其主要原理是:
1、通过对需要编码的字符串resource中字符char的出现频率进行统计得出相应的映射关系,
2、依据字符出现的频率对字符char进行编码 code
3、构建哈夫曼二叉树HuffmanTree(二叉树的节点data(char(字符串中出现的每一个char)、weight字符出现的权重、left,right左右子节点、节点data的对应编码code)),且二叉树的排序的规则以字符出现的权重进行排序
4、将字符串resource 和 HuffmanTree 的字符编码字典进行字符的迭代编码从而形成一串01的字符串
5、解码的过程是通过将01的串进行迭代,并构建一个临时的缓存区st,将011010…串的字符进行st入栈,并将st的串和HuffmanTree 中节点的code进行编码比对,当比对结果是true时,则表示当前的code对应是节点的data,从而将st清空,并继续对0110001…进行迭代解码
实例
统计字符的概率
| 字符 概率 | |
|---|---|
| a | 0.12 |
| b | 0.40 |
| c | 0.15 |
| d | 0.05 |
| e | 0.25 |
字符编码
我们现在要将文本编码成0/1序列从而使得计算机能够进行读取和计算。为了保证每个字符的独一性,所以我们给予不同的的字符以不同的编码。如果给每个字符赋予等长的编码的话,会使得平均的编码长度过长,影响计算时的性能,浪费计算机的资源(定长编码的缺点)。这时我们就想到了变长编码,理所当然的,给出现概率较大的字符赋予##### 统计字符的概率,概率较小的字符赋予较长的编码,这样在计算的时候不就可以节省很多时间了吗?可这样我们又面临到了一个巨大的问题,我们来看下面这种情况,我们对字符进行编码:
| 字符 | 概率 | 编码 |
|---|---|---|
| a | 0.12 | 01 |
| b | 0.40 | 0 |
| c | 0.15 | 00 |
| d | 0.05 | 10 |
| e | 0.25 | 1 |
构建哈夫曼树
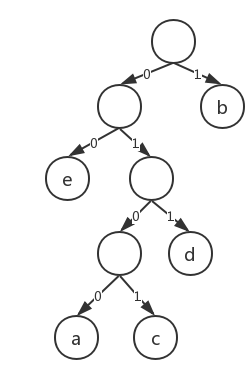
假设现在文本中的字符是bcd,转换之后的0/1序列为00010,可我们要在转换成文本的时候究竟是把第一位的0读作b还是把前两位的00读作c呢?为了解决这个问题,就又有了前缀码的概念。顾名思义,前缀码的含义就是任意字符的编码都不是其他字符编码的前缀。那么该如何形成前缀码呢?首先我们要构造一棵二叉树,指向左孩子的"边"记作0,指向右孩子的点记作“1”,叶子节点为代编码的字符,出现概率越大的字符离根的距离就越近。
代码实现
定义树的节点
public class Node<T> implements Comparable<Node<T>> {
private T data;
private double weight;
private Node<T> left;
private Node<T> right;
String code;
public Node(T data, double weight){
this.data = data;
this.weight = weight;
this.code = "";
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public double getWeight() {
return weight;
}
public void setWeight(double weight) {
this.weight = weight;
}
public Node<T> getLeft() {
return left;
}
public void setLeft(Node<T> left) {
this.left = left;
}
public Node<T> getRight() {
return right;
}
public void setRight(Node<T> right) {
this.right = right;
}
public String getCode(){
return code;
}
public void setCode(String str){
code = str;
}
@Override
public String toString(){
return "data:"+this.data+";weight:"+this.weight+";code: "+this.code;
}
@Override
public int compareTo(Node<T> other) {
if(other.getWeight() > this.getWeight()){
return 1;
}
if(other.getWeight() < this.getWeight()){
return -1;
}
return 0;
}
}
定义哈夫曼树。(主要包含两个方法createTree(),breadth())
createTree方法返回一个结
- createTree方法返回一个结点,也就是根结点。首先把所有的nodes结点类都储存在一个List中,利用Collections的sort方法把结点按照权值的大小按照从大到小的顺序进行排列。然后把List中的倒数第二个元素设为左孩子,倒数第一个元素设为右孩子。这个时候要注意:它们的双亲结点为以左右孩子的权值的和作为权值的构成的新的结点。然后删去左右孩子结点,将形成的新结点加入的List中。直到List中只剩下一个结点,也就是根结点时为止
- 广度遍历的方法,在遍历的时候,每遍历到左孩子,就把结点中的code变量加上“0”,这里的加不是简单的数学运算,而是字符串的叠加。每遍历到右孩子,就把结点中的code变量加上“1”,这样遍历过一遍后,叶子结点中的code储存的就是对应的哈夫曼编码值。
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Queue;
public class HuffmanTree {
/**
* 构建哈夫曼树
* @param nodes
* @return
*/
public <T> Node<T> createTree(List<Node<T>> nodes) {
while (nodes.size() > 1) {
Collections.sort(nodes);
Node<T> left = nodes.get(nodes.size() - 2);
left.setCode(0 + "");
Node<T> right = nodes.get(nodes.size() - 1);
right.setCode(1 + "");
Node<T> parent = new Node<T>(null, left.getWeight() + right.getWeight());
parent.setLeft(left);
parent.setRight(right);
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 在构建哈夫曼树的类中还实现了一个广度遍历的方法,在遍历的时候,每遍历到左孩子,就把结点中的code变量加上“0”,这里的加不是简单的数学运算,而是字符串的叠加。每遍历到右孩子,就把结点中的code变量加上“1”,这样遍历过一遍后,叶子结点中的code储存的就是对应的哈夫曼编码值。
* @param root
* @return
*/
public <T> List<Node<T>> breadth(Node<T> root) {
List<Node<T>> list = new ArrayList<Node<T>>();
Queue<Node<T>> queue = new ArrayDeque<Node<T>>();
if (root != null) {
queue.offer(root);
root.getLeft().setCode(root.getCode() + "0");
root.getRight().setCode(root.getCode() + "1");
}
while (!queue.isEmpty()) {
list.add(queue.peek());
Node<T> node = queue.poll();
if (node.getLeft() != null)
node.getLeft().setCode(node.getCode() + "0");
if (node.getRight() != null)
node.getRight().setCode(node.getCode() + "1");
if (node.getLeft() != null) {
queue.offer(node.getLeft());
}
if (node.getRight() != null) {
queue.offer(node.getRight());
}
}
return list;
}
}
处理需要编码的字符串
public static class readtxt {
char[] chars = new char[]{'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s'
,'t','u','v','w','x','y','z','P',' '};
int[] number = new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
public String txtString(File file){
StringBuilder result = new StringBuilder();
try{
BufferedReader br = new BufferedReader(new FileReader(file));//构造一个BufferedReader类来读取文件
String s = null;
while((s = br.readLine())!=null){//使用readLine方法,一次读一行
result.append(System.lineSeparator()+s);
num(s);
}
br.close();
}catch(Exception e){
e.printStackTrace();
}
return result.toString();
}
public String txtString(String reusrce){
StringBuilder result = new StringBuilder();
try{
BufferedReader br = new BufferedReader(new FileReader(file));//构造一个BufferedReader类来读取文件
num(reusrce);
}catch(Exception e){
e.printStackTrace();
}
return result.toString();
}
public void num(String string){
for(int i = 0;i<28;i++){
int temp = 0;
for(int j = 0;j<string.length();j++){
if(string.charAt(j) == chars[i])
temp++;
}
number[i] += temp;
}
}
public int[] getNumber(){
return number;
}
public char[] getChars(){
return chars;
}
}
测试方法
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.util.ArrayList;
import java.util.List;
public class TestMain {
public static void main(String[] args) {
// File file = new File("F:\\input1\\input1.txt");
//编码的原始数据
String temp = "please go to the attendance management to update in time when the national holidays change";
//文本进行处理,定义两个数组获得文本中出现的字符和字符出现的次数
readtxt read = new readtxt();
// String temp = read.txtString(file);
System.out.println(temp);
System.out.println("***************");
int[] num = read.getNumber();
char[] chars = read.getChars();
//利用一个循环把对应的data值和weight权重值构造成结点加入到list中。
List<Node<String>> list = new ArrayList<>();
for(int i = 0;i<28;i++){
System.out.print(chars[i]+":"+num[i]+" ");
list.add(new Node<String>(chars[i]+"",num[i]));
}
//构建哈夫曼树并得到根结点。
HuffmanTree huffmanTree = new HuffmanTree();
Node<String> root = huffmanTree.createTree(list);
List<Node<String>> list2 = new ArrayList<>();
list2=huffmanTree.breadth(root);
List<String> list3 = new ArrayList<>(list2.size());
List<String> list4 = new ArrayList<>(list2.size());
for(int i = 0;i<list2.size();i++){
if(list2.get(i).getData()!=null) {
Node<String> node = list2.get(i);
list3.add(node.getData());
list4.add(node.getCode());
}
}
String result = "";
for(int i = 0;i<temp.length();i++){
for(int j = 0;j<list3.size();j++){
if(temp.charAt(i) == list3.get(j).charAt(0)){
result += list4.get(j);
}
}
}
System.out.println("哈夫曼算法编码结果");
System.out.println(result);
List<String> list5 = new ArrayList<>(result.length());
for(int i = 0;i<result.length();i++){
list5.add(result.charAt(i)+"");
}
String temp2 = "";
String temp3 = "";
while (list5.size()>0){
temp2 = temp2+"" +list5.get(0);
list5.remove(0);
for(int i=0;i<list4.size();i++){
if (temp2.equals(list4.get(i))) {
temp3 = temp3+""+list3.get(i);
temp2 = "";
}
}
}
System.out.println("***********");
System.out.println(temp3);
}
}
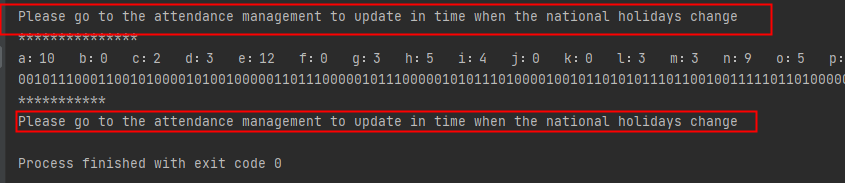
运行结果