根据教学大纲

?排序分三种存储结构
顺序存储结构,链式存储结构,索引存储结构
数据结构与算法系列--十大排序(附动态图解) - 知乎 (zhihu.com)
?
目录
一、直接插入排序
思想:
?当插入第i (i >=1) 个对象时, 前面的V[0], V[1], …, V[i-1]已经排好序。这时, 用V[i]的排序码与V[i-1], V[i-2], …的排序码顺序进行比较, 找到插入位置即将V[i]插入, 原来位置上的对象向后顺移。
?
?直接插入排序是一种稳定的排序方法。
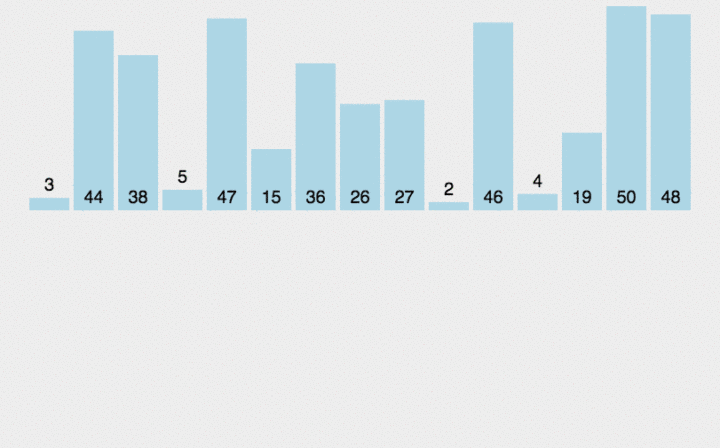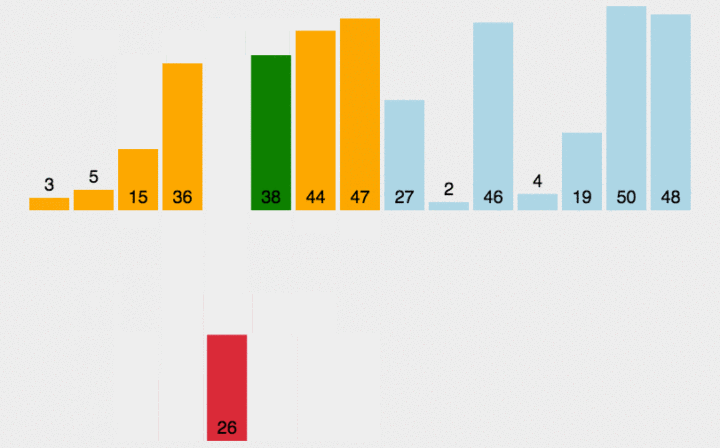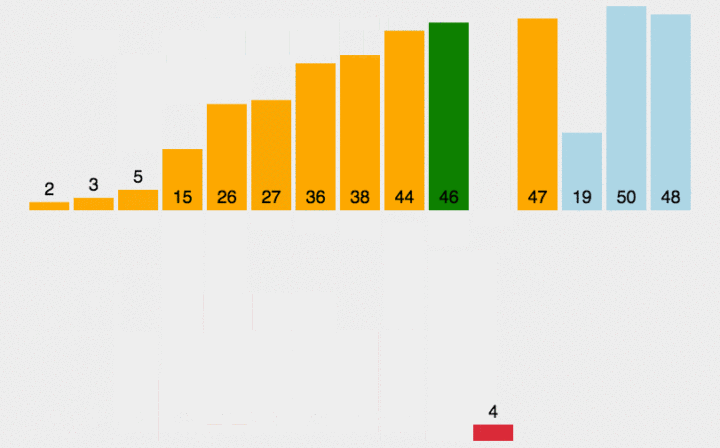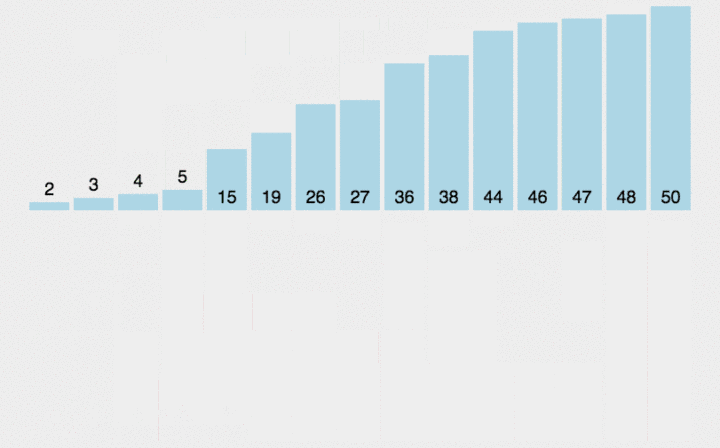
代码实现(顺序存储结构)
void insertsort(int a[],int n) {
if (n == 0) {
cout << "无法排序" << endl;
exit(0);
}
int current;
for (int i = 0; i < n-1; i++) {//执行n-1趟插排
current = a[i + 1];//每次对未排序好的下一个进行排序
int preIndex = i;
while (preIndex >= 0 && current < a[preIndex]) {//把current元素插入到已经排好序的序列
a[preIndex + 1] = a[preIndex];
preIndex--;
}
a[preIndex + 1] = current;//挖出的空后移
}
}链式存储结构(现在暂时想到用两个链表进行操作)
void listinsert(LinkNode head) {
if (head == NULL || head->next == NULL)
return;
LinkNode pre = head;//pre指向已经有序的节点
LinkNode cur = head->next;//cur指向待排序的节点
LinkNode aux = new ListNode;//辅助节点
aux->data = -99999;
aux->next = head;
while (cur != NULL) {
if (cur->data < pre->data) {
//先把cur节点从当前链表中删除,然后再把cur节点插入到合适位置
pre->next = cur->next;
//从前往后找到l2.val>cur.val,然后把cur节点插入到l1和l2之间
LinkNode l1 = aux;
LinkNode l2 = aux->next; //快慢指针
while (cur->data > l2->data) {
l1 = l2;
l2 = l2->next;
}
//把cur节点插入到l1和l2之间
l1->next = cur;
cur->next = l2;//插入合适位置
cur = pre->next;//指向下一个待处理节点
}
else {
pre = cur;
cur = cur->next;
}
}
}二、折半插入排序(手工题)
思想:折半搜索比顺序搜索查找快, 所以折半插入排序就平均性能来说比直接插入排序要快。
折半查找排序是基于直接插入排序中的查找过程利用二分查找进行工作?
具体的我不去找图描述了,和上面动态图一样,只不过在查找过程中的区别
三、希尔排序(手工题)
核心关键是缩小增量排序
设待排序对象序列有 n 个对象, 首先取一个整数 gap < n 作为间隔,? 将全部对象分为 gap 个子序列,? 所有距离为 gap 的对象放在同一个子序列中,? 在每一个子序列中分别施行直接插入排序。然后缩小间隔 gap, 例如取 gap = gap/2[向下取整],重复上述的子序列划分和排序工作。直到最后取 gap == 1, 将所有对象放在同一个序列中排序为止。
上面难理解有个无敌网站
手工图(间隔为gap的进行比较排序)
 ?
?
算法代码
void ShellSort (SqList &L, int dlta[], int t)
{ // 增量为dlta[]的希尔排序
for (k=0; k<t; ++t)
ShellInsert(L, dlta[k]);
//一趟增量为dlta[k]的插入排序
}
void ShellInsert ( SqList &L, int dk ) {
for ( i=dk+1; i<=n; ++i )
if ( L.r[i].key< L.r[i-dk].key) {
L.r[0] = L.r[i]; // 暂存在L.r[0]
for (j=i-dk;j>0&&(L.r[0].key<L.r[j].key); j-=dk)
L.r[j+dk] = L.r[j]; // 记录后移,查找插入位置
L.r[j+dk] = L.r[0]; // 插入
} // if
} // ShellInsert
?四、直接选择排序
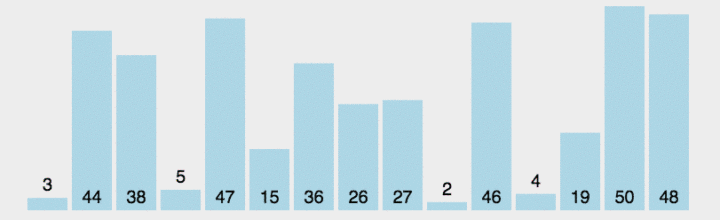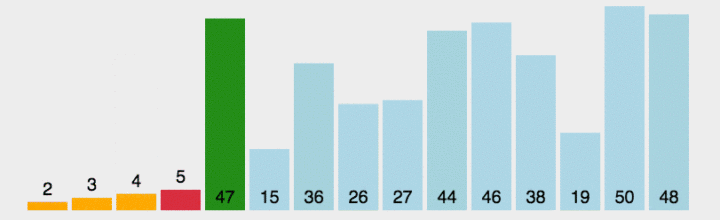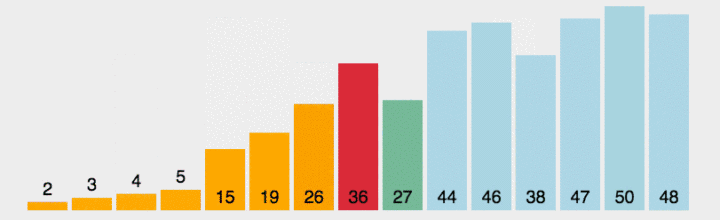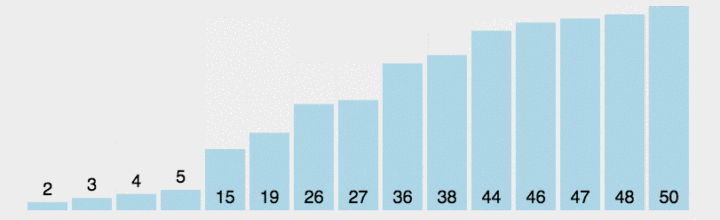
?算法代码
顺序存储结构?
void selectsort(int v[], int n)
{
if (n == 0)
return;
for (int i = 0; i < n; i++) {
int minIndex = i;
for (int j = i; j < n; j++) {
if(v[j] < v[minIndex]) //找到最小的数
minIndex = j; //将最小数的索引保存
}
int temp = v[minIndex];
v[minIndex] = v[i];
v[i] = temp;//交换
}
}链式
之前有写过,还是不复制粘贴了
五、堆排序(大顶堆)
关键思想:
根据初始输入数据,利用堆的调整算法形成初始堆
通过一系列的对象交换和重新调整堆进行排序。
堆(树形结构应用)_find it %%的博客-CSDN博客
?可以看下面视频加强理解
期中考试考了手工题,可以在之前博客看看
算法代码
很简洁(很难记)
int* HeapSort(int array[],int len) {
if (len < 1) return array;
//1.构建一个最大堆
buildMaxHeap(array);
//2.循环将堆首位(最大值)与末位交换,然后在重新调整最大堆
while (len > 0) {
swap(array, 0, len - 1);
len--;
adjustHeap(array, 0);
}
return array;
}
/*建立最大堆*/
void buildMaxHeap(int array[]) {
//从最后一个非叶子节点开始向上构造最大堆
for (int i = (len - 1) / 2; i >= 0; i--) {
adjustHeap(array, i);
}
}
void adjustHeap(int array[], int i) {
int maxIndex = i;
//如果有左子树,且左子树大于父节点,则将最大指针指向左子树
if (i * 2 < len && array[i * 2] > array[maxIndex])
maxIndex = i * 2;
//如果有右子树,且右子树大于父节点,则将最大指针指向右子树
if (i * 2 + 1 < len && array[i * 2 + 1] > array[maxIndex])
maxIndex = i * 2 + 1;
//如果父节点不是最大值,则将父节点与最大值交换,并且递归调整与父节点交换的位置。
if (maxIndex != i) {
swap(array, maxIndex, i);
adjustHeap(array, maxIndex);
}
}六、冒泡排序
这个太简单了,大一写到现在,默都能默写出来
但是冒泡排序是快排的基石(同一类型)
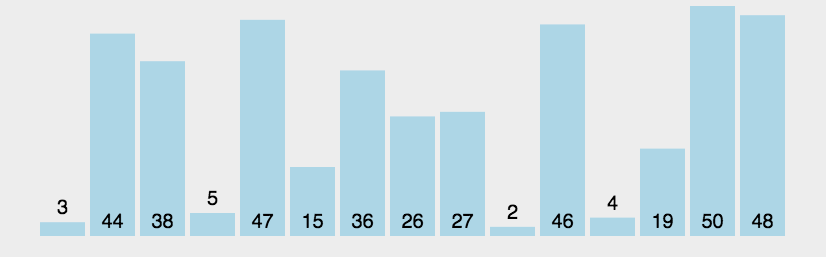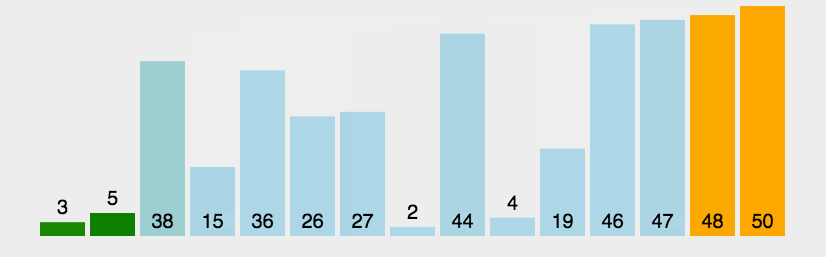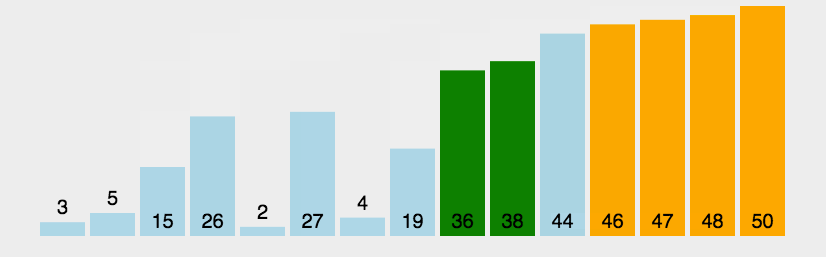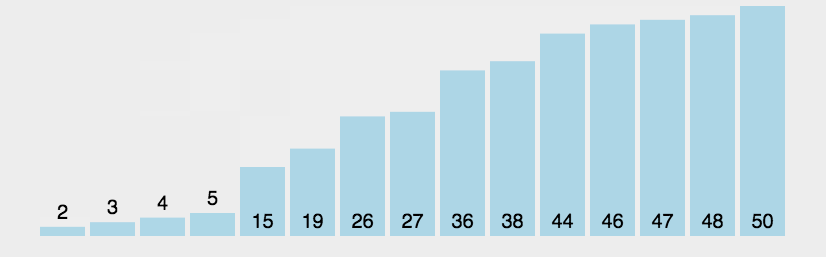
链表的冒泡排序怎么弄?交换节点值,不要改链
七、快速排序(每年必考)
思想:
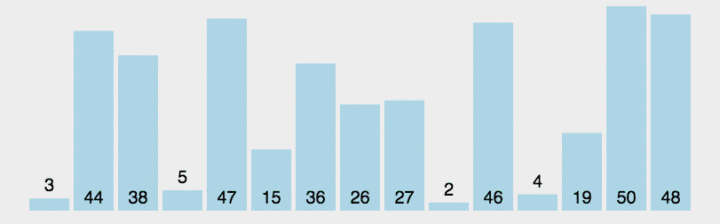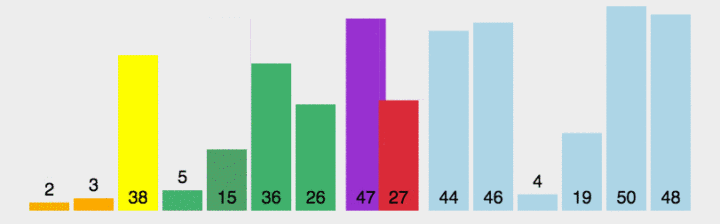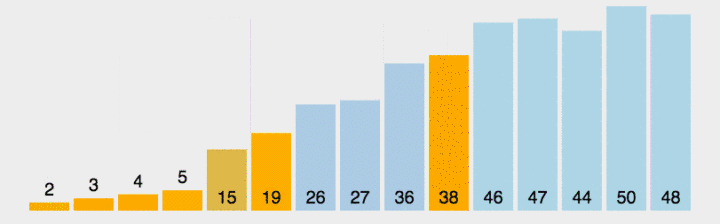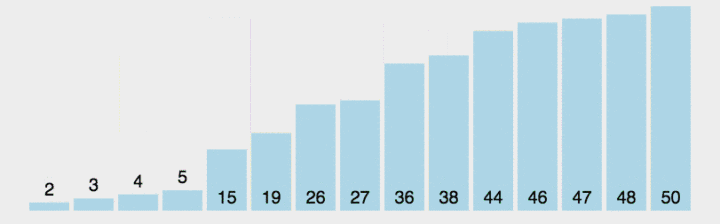
?先搞清除一趟快排
目标:找一个记录,以它的关键字作为“枢轴”,凡其关键字<?枢轴的记录均移动至该记录之前,反之,凡关键字?>?枢轴的记录均移动至该记录之后。
致使一趟排序之后,记录的无序序列R[s..t]将分割成两部分:R[s..i-1]和R[i+1..t], 且?
?????? R[j].key? ≤?R[i].key ≤ R[j].key
? ? ? ?(s≤j≤i-1)??? 枢轴 ? ? ? ?(i+1≤j≤t)
例子:
经过“一次划分” ,将关键字序列
?????????????? 52, 49, 80, 36, 14,? 58, 61, 97, 23, 75?
调整为:? ?23, 49, 14, 36, (52) 58, 61, 97, 80, 75
实现一趟划分的代码
int Partition (RedType R[], int low, int high) {
R[0] = R[low]; pivotkey = R[low].key; // 枢轴
while (low<high) {
while(low<high&& R[high].key>=pivotkey)
-- high; // 从右向左搜索
R[low] = R[high];
while (low<high && R[low].key<=pivotkey)
++ low; // 从左向右搜索
R[high] = R[low];
}
R[low] = R[0];
return low;
}// Partition
对无序的记录序列进行“一次划分”,之后分别对分割所得两个子序列“递归”进行快速排序。
代码实现
/*
第一次调用函数 Qsort 时
待排序记录序列的上、下界分别为 1 和 L.length。
*/
void QuickSort( SqList & L) {//总接口
// 对顺序表进行快速排序
QSort(L.r, 1, L.length);
}
void QSort (RedType & R[], int s, int t ) {
// 对记录序列R[s..t]进行快速排序
if (low<high) { // 长度大于1
pivotloc = Partition(R, s, t);
// 对 R[s..t] 进行一次划分
QSort(R, s, pivotloc-1);
// 对低子序列递归排序,pivotloc是枢轴位置
QSort(R, pivotloc+1, t); // 对高子序列递归排序
}
}
八、二路归并(归并排序手工题)
思想:
两路归并 (2-way merging)原始序列initList[ ]中两个有序表 initList[l] … initList[m]和initList[m+1] … initList[n],它们可归并成一个有序表, 存于另一对象序列mergedList的 l … n 中。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
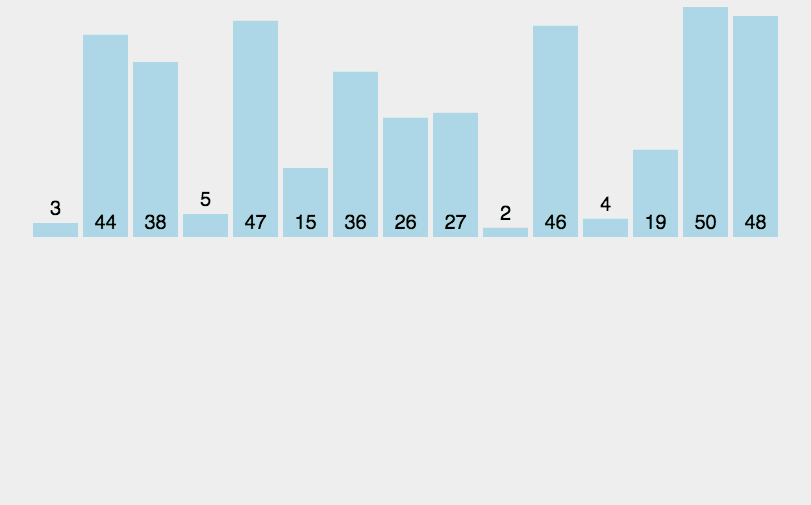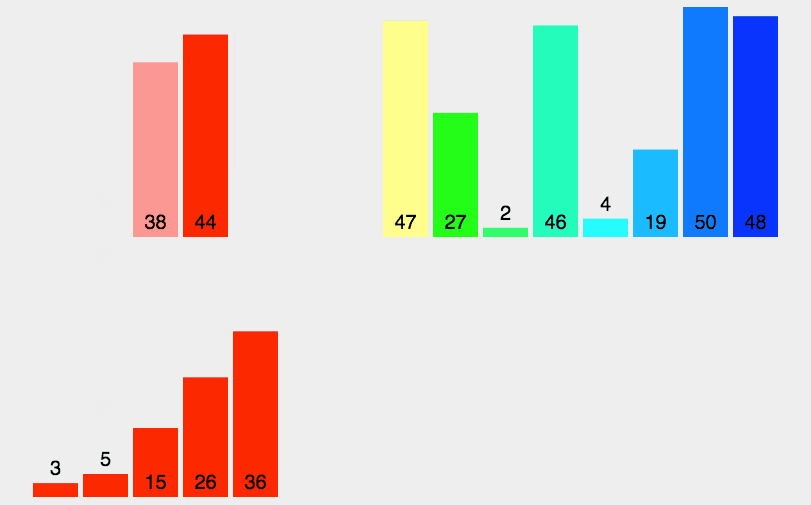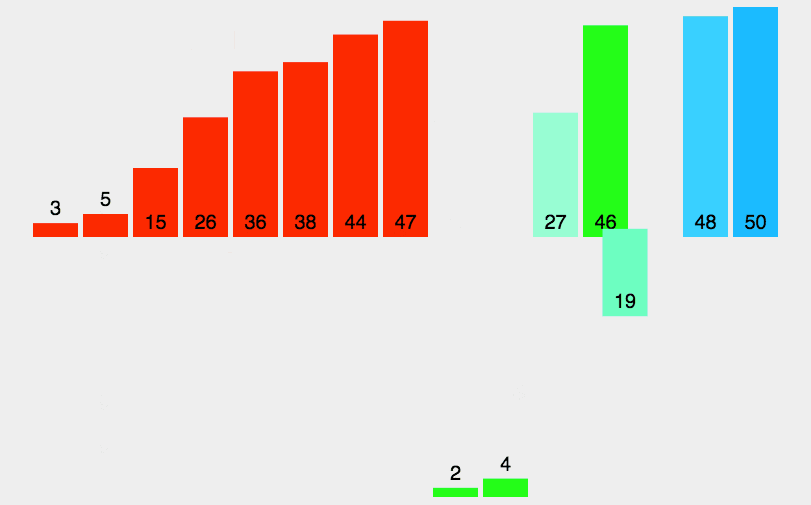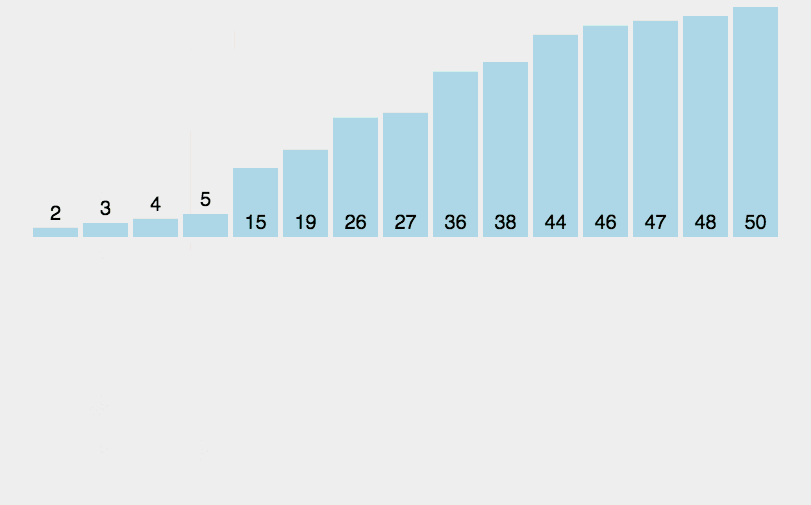
九、桶排序
思想:根据数据之间的某种关系进行分类(把一群有关系的数据放进一个桶)桶内排好序,整体就排序完了,例如一个桶的树范围是0~10,另外一个桶是11~20这样子;
MSD法如下:
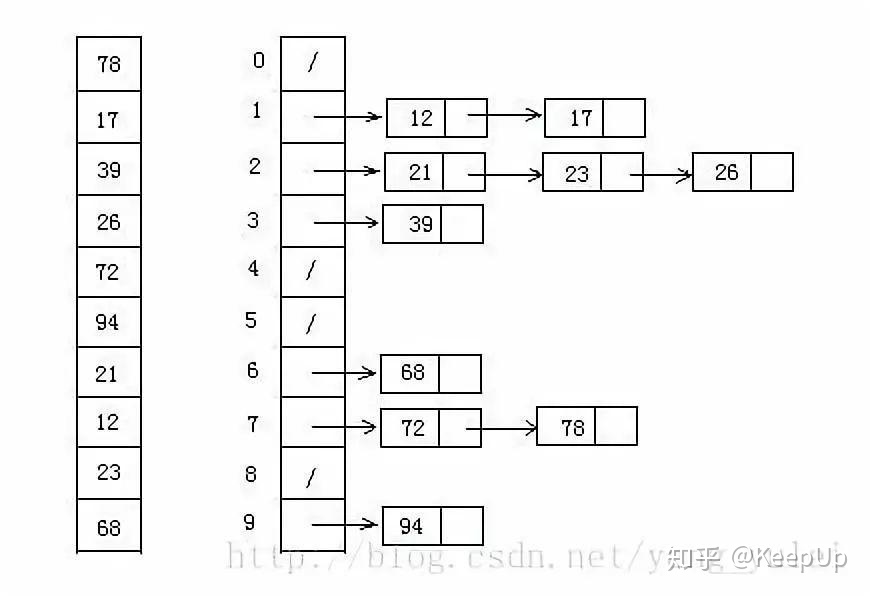
?最高位优先MSD法:
????? 先对K0进行排序,并按 K0 的不同值将记录序列分成若干子序列之后,分别对 K1 进行排序,...…, 依次类推,直至最后对最次位关键字排序完成为止。
最低位优先LSD法:
?先对 Kd-1 进行排序,然后对 Kd-2?? 进行排序,依次类推,直至对最主位关键字 K0 排序完成为止。
十、基数排序
?思想:
基数排序也是非比较的排序算法,对每一位进行排序,从最低位开始排序,复杂度为O(kn),为数组长度,k为数组中的数的最大的位数;
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。

总结
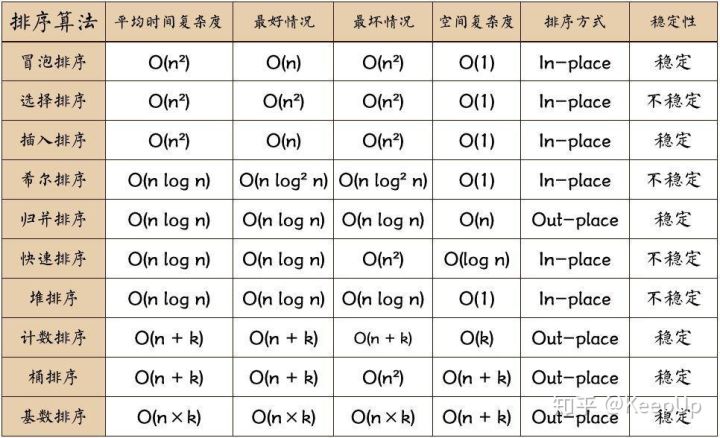
?
?