[数据结构与算法]表达式二叉树的构造（java实现）

一、树的创建

1.文字描述

1、开辟两个链表，一个numList存放运算数，一个opeList存放运算符，初始化String number = “”；通过字符串拼接来保存两位及以上的运算数
2、遍历算术表达式。
?1）若遇到运算数，通过字符串拼接保存在 number中 继续遍历
?2）若遇到运算符，分别将number放入numList，运算符放入opeList
?3）number = “”;
3、将算数表达式的最后一个运算数添加到numList中，这一步是因为当我们遍历到表达式的最后一位时，仅仅将其拼接保存在number中，因为不会再往后遍历，也就是不会再遇到运算符，因此2.2添加步骤尚未执行
通过上面的步骤，我们已经将运算数和运算符分别放到了两个链表中，接下来就是遍历运算符opeList链表，创建树
4、循环创建二叉树，直到运算符链表opeList为空
?1）访问并移除opeList队头元素A
?2）从运算数numList中按顺序访问并移除两个运算数B C
?3）分别将B C 设置成A的左右子树
?4）将A放到numList的第一个元素
?5）重复步骤4

2.图文描述

例如表达式：1 + 2 * 3 - 4 / 5

通过1-3步骤后

链表numList和opeList的内容如下

执行4.1步骤

步骤4.2

步骤4.3

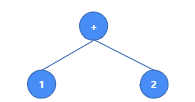
此时链表numList和opeList的内容如下

如此反复

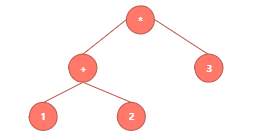
这样 表达式的一棵二叉树就创建好了。

下面展示使用中序遍历对二叉树进行遍历的结果

二、完整代码

在写算数表达式二叉树的时候临时想了一下如何实现计算算术表达式，方法也附上。

package com.xx.exp06;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Stack;

/**
 * @author 谢鑫
 * @version 1.0
 */
public class Exp06_02 {
    public static void main(String[] args) {
        String str = "1+2*3-4/5";
        System.out.println("算数表达式：" + str);
        ariBinarytTree ariBinarytTree = new ariBinarytTree();
        ariBinarytTree.createTree(str);
        System.out.print("对应的二叉树中序遍历输出：");
        ariBinarytTree.infixOrder();
        System.out.println();

        ariBinarytTree.calResult(str);


    }
}

//算术表达式二叉树
class ariBinarytTree {

    //定义一个根节点
    Node02 root = null;


    public void createTree(String aString) {
        LinkedList<Node02> numList = new LinkedList<>(); //存放运算数
        LinkedList<Node02> opeList = new LinkedList<>(); //存放运算符

        char[] c = aString.toCharArray(); //将字符串字符数组化
        int len = c.length;
        String number = ""; //用于拼接两位及以上的整数

        for (int i = 0; i < len; i++) {
            if (c[i] >= '0' && c[i] <= '9') { //为数字
                number += c[i]; //将遍历所得整数拼接到number字符串中
            } else { //为运算符
                //分别将遍历所得的整数与运算符加到列表中
                numList.add(new Node02(number));
                opeList.add(new Node02(c[i] + ""));

                number = ""; //将number置空， 继续遍历
            }
        }
        numList.add(new Node02(number)); //将表达式最后一个整数添加numList中 因为当i = 9时 并不会再进入到else语句中添加

        Node02 temp = null; //用于存放取出的运算符 -> 构建树
        while (!opeList.isEmpty()) { //循环创建二叉树 直到存放运算符的队列opeList为空
            temp = opeList.poll(); //访问并移除队头元素

            temp.setLeft(numList.poll()); //设置左子树
            temp.setRight(numList.poll()); //设置右子树

            root = temp; //将temp设置成根节点
            numList.add(0, temp); //将temp放置在队头
        }
    }

    //计算表达式结果
    public void calResult(String aString) {

        if (aString.length() == 0) {
            System.out.println("表达式为空, 无法计算！");
            return;
        }

        Stack<Node02> numStack = new Stack<>(); //存放运算数的栈
        Stack<Node02> opeStack = new Stack<>(); //存放运算符的栈

        char[] c = aString.toCharArray();
        int len = c.length;
        String number = "";
        Node02 temp = null; //用于比较运算符的优先级时保存栈头运算符

        for (int i = 0; i < len; i++) {
            if (c[i] >= '0' && c[i] <= '9') {
                number += c[i];
            } else {
                numStack.add(new Node02(number)); // number 添加到运算数栈中
                Node02 aNode02 = new Node02(c[i] + "");
                if (opeStack.isEmpty()) { //若运算符栈为空
                    opeStack.add(aNode02); //则直接添加
                } else { // 运算符栈不为空 则需要比较运算符的优先级
                    temp = opeStack.peek(); //访问栈头运算符但不移除
                    if (aNode02.getPriority() < temp.getPriority()) { //如果要添加的运算符优先级低于栈头运算符优先级
                        //弹出运算数栈两个节点
                        Node02 node01 = numStack.pop();
                        Node02 node02 = numStack.pop();

                        Node02 tempOpe = opeStack.pop();
                        //进行运算
                        if (tempOpe.getElement().equals("*")) {
                            double tempRes = Double.parseDouble(node01.getElement()) * Double.parseDouble(node02.getElement()); //将字符串转换成int后计算
                            numStack.push(new Node02(tempRes + ""));
                            opeStack.add(aNode02);
                        } else if (tempOpe.getElement().equals("/")) {
                            double tempRes = Double.parseDouble(node01.getElement()) / Double.parseDouble(node02.getElement());
                            numStack.push(new Node02(tempRes + ""));
                            opeStack.add(aNode02);
                        }
                    } else { //要添加的运算符优先级高于栈头运算符优先级
                        opeStack.add(aNode02); //则直接添加
                    }
                }
                number = "";
            }
        }
        //添加最后一个运算数
        numStack.add(new Node02(c[len - 1] + ""));


        while (!opeStack.isEmpty()) {
            Node02 tempOpe = opeStack.pop();

            //被减数与被除数应该是第二个弹出的运算数 正负问题
            Node02 node02 = numStack.pop();
            Node02 node01 = numStack.pop();

            if (tempOpe.getElement().equals("*")) {
                double tempRes = Double.parseDouble(node01.getElement()) * Double.parseDouble(node02.getElement());
                numStack.add(new Node02(tempRes + ""));
            } else if (tempOpe.getElement().equals("/")) {
                double tempRes = Double.parseDouble(node01.getElement()) / Double.parseDouble(node02.getElement());
                numStack.add(new Node02(tempRes + ""));
            } else if (tempOpe.getElement().equals("+")) {
                double tempRes = Double.parseDouble(node01.getElement()) + Double.parseDouble(node02.getElement());
                numStack.add(new Node02(tempRes + ""));
            } else if (tempOpe.getElement().equals("-")) {
                double tempRes = Double.parseDouble(node01.getElement()) - Double.parseDouble(node02.getElement());
                numStack.add(new Node02(tempRes + ""));
            }
        }
        System.out.println("表达式的结果为：" + numStack.pop());

    }

    //中序遍历
    public void infixOrder() {
        if (this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("此二叉树为空, 无法完成中序遍历！");
        }
    }
}

class Node02 {
    private String element;
    private Node02 left;
    private Node02 Right;

    public Node02(String element) {
        this.element = element;
    }

    //返回运算符的运算优先级
    public int getPriority() {
//        //运算符为+ -
//        if (this.element == "+" || this.element == "-") {
//            return 1;
//        }
//        //运算符为* /
//        if (this.element == "*" || this.element == "/"){
//            return 2;
//        }
//       throw new RuntimeException("非运算符！无法获取优先级！");

        switch (this.element) {
            case "+":
                return 1;
            case "-":
                return 1;
            case "*":
                return 2;
            case "/":
                return 2;
        }
        throw new RuntimeException("非运算符！无法获取优先级！");
    }

    public String getElement() {
        return element;
    }

    public void setElement(String element) {
        this.element = element;
    }

    public Node02 getLeft() {
        return left;
    }

    public void setLeft(Node02 left) {
        this.left = left;
    }

    public Node02 getRight() {
        return Right;
    }

    public void setRight(Node02 right) {
        Right = right;
    }

    public void infixOrder() {
        //遍历左子树
        if (this.getLeft() != null) {
            this.getLeft().infixOrder();
        }
        //输出当前节点
        System.out.print(this + " ");
        //遍历右子树
        if (this.getRight() != null) {
            this.getRight().infixOrder();
        }

    }

    @Override
    public String toString() {
        return element + "";
    }

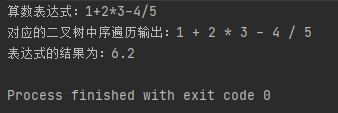
三、总结

??在写计算算数表达式的时候确实郁闷了，由于没有正确运用equals()方法和==符号，前期遇到各种报错，导致一路写下来计算表达式这个方法虽然实现了功能，但代码格外冗沉。

运用equals() 和 ==
1.对基本类型而言，使用==进行比较，是直接比较两个数据类型之间的数值

2.对于引用类型而言，使用==进行比较，是比较的两个数据类型之间的地址

代码一：

 	   String str1 = "hello";
       String str2 = "hello";

代码二：

	   String str3 = "hello";
       String str4 = new String("hello");

问题在于 代码一的str1 str2均指向常量区的同一个hello字符串 运用==运算符比较，返回自然为true
而代码二的str3指向常量区的hello字符串，而str4则指向堆区 二者的地址显然不相同！

在写代码过程中 对于字符串 我们既可能使用new运算符在堆区开辟空间，也有可能直接指向常量区，故在平常写代码的过程中，比较String类时，尽量使用equals()方法 避免不必要的麻烦。

感谢观看！还望指出文中的错误！
代码需要沉淀
点个赞吧！